Equation Of Tangent And Normal To The Curve

Tangents And Normals Equation Of Tangent And Normal To A Curve Normal to a curve the normal to a curve at a point \(p\) along its length is the line which passes through point \(p\) and is perpendicular to the tangent at \(p\) say the curve has equation \(y = f(x)\), then its gradient at a point \(p\begin{pmatrix}a,b\end{pmatrix}\) along its length is equal to: \[f'(a)\] since the normal is perpendicular to the tangent, its gradient is the negative. Therefore, the equation of the normal to the curve at (1, 1) is y x =0. practice problems. solve the following problems: calculate the slope of the tangent to the curve y=x 3 x at x=2. determine the slope of the tangent to the curve y=x 3 3x 2 at the point whose x coordinate is 3. find the equation of tangent and normal to the curve y = x 3 at.

Calculus Equations Of Tangent And Normal To A Curve Youtube Examples on tangents and normals. example 1: find the equation of tangent and normal to the circle x 2 y 2 = 5, at the point (2, 3). solution: the given equation of the circle is x 2 y 2 = 5. the slope of the tangent is obtained by taking the derivative of the above expression with respect to x. 2x 2y.dy dx = 0. Tangents and normals. mc ty tannorm 2009 1. this unit explains how differentiation can be used to calculate the equations of the tangent and normal to a curve. the tangent is a straight line which just touches the curve at a given point. the normal is a straight line which is perpendicular to the tangent. Suppose f(x) = cos x f (x) = cos x. find the equation of the line that is normal to the function at x = π 6 x = π 6. step 1. find the point on the function. f(π 6) = cos π 6 = 3√ 2 f (π 6) = cos π 6 = 3 2. the point is (π 6, 3√ 2) (π 6, 3 2). step 2. find the value of the derivative at x = π 6 x = π 6. Note 1: as we discussed before (in slope of a tangent to a curve), we can find the slope of a tangent at any point (x, y) using `dy dx`. note 2: to find the equation of a normal, recall the condition for two lines with slopes m 1 and m 2 to be perpendicular (see perpendicular lines): m 1 × m 2 = −1. applications.
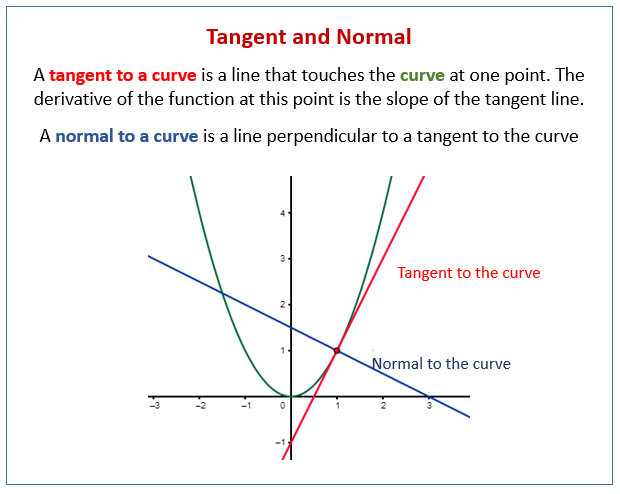
Differentiation Tangents And Normals Examples Worksheets Videos Suppose f(x) = cos x f (x) = cos x. find the equation of the line that is normal to the function at x = π 6 x = π 6. step 1. find the point on the function. f(π 6) = cos π 6 = 3√ 2 f (π 6) = cos π 6 = 3 2. the point is (π 6, 3√ 2) (π 6, 3 2). step 2. find the value of the derivative at x = π 6 x = π 6. Note 1: as we discussed before (in slope of a tangent to a curve), we can find the slope of a tangent at any point (x, y) using `dy dx`. note 2: to find the equation of a normal, recall the condition for two lines with slopes m 1 and m 2 to be perpendicular (see perpendicular lines): m 1 × m 2 = −1. applications. So if the gradient of the tangent at the point (2, 8) of the curve y = x 3 is 12, the gradient of the normal is 1 12, since 1 12 × 12 = 1 . the equation of the normal at the point (2, 8) is therefore: y 8 = 1 12 (x 2) hence the equation of the normal at (2,8) is 12y x = 98 . tangents and normals a level maths revision section looking. Find a line that is perpendicular to the tangent line to an equation at a point. find the normal line to the graph of a function at a point: normal line to y=sin (2x) 2cos (x) at x=pi 4. find the normal to a curve specified by an equation: normal to 3x^2 2xy y^2=1 at x=0, y=1. find the normal to a surface: normal to sin (x y) at x=0, y=1.

Equations Of Tangent And Normal Lines At A Given Point Youtube So if the gradient of the tangent at the point (2, 8) of the curve y = x 3 is 12, the gradient of the normal is 1 12, since 1 12 × 12 = 1 . the equation of the normal at the point (2, 8) is therefore: y 8 = 1 12 (x 2) hence the equation of the normal at (2,8) is 12y x = 98 . tangents and normals a level maths revision section looking. Find a line that is perpendicular to the tangent line to an equation at a point. find the normal line to the graph of a function at a point: normal line to y=sin (2x) 2cos (x) at x=pi 4. find the normal to a curve specified by an equation: normal to 3x^2 2xy y^2=1 at x=0, y=1. find the normal to a surface: normal to sin (x y) at x=0, y=1.

Comments are closed.