Equation Of A Circle With Radius And Center Tessshebaylo Finding the center and radius of a circle you. circle equations mathbitsnotebook geo. the center radius form for a circle few basic questions example 2 you. finding the center and radius of a circle expii. identifying the center radius to graph a circle given its equation in standard form geometry study com. equation of a circle math monks. Free circle equation calculator calculate circle's equation using center, radius and diameter step by step.
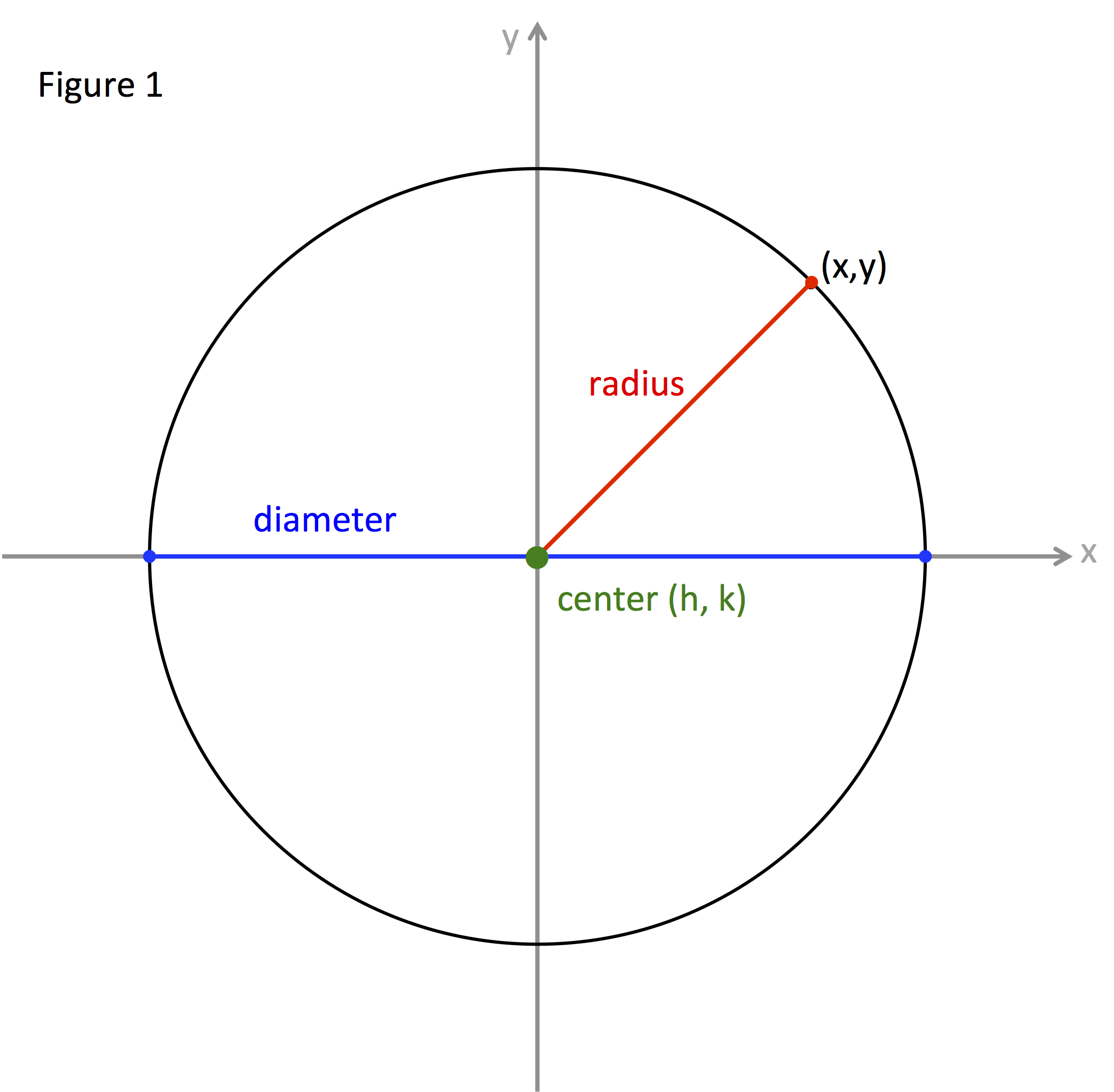
Equation Of A Circle Using Radius And Center Tessshebaylo In this lesson we’ll look at how to write the equation of a circle in standard form in order to find the center and radius of the circle. the standard form for the equation of a circle is (x h)^2 (y k)^2=r^2, where r is the radius and (h,k) is the center. sometimes in order to write the equation of a circle in standard form, you’ll need to. The equation for a circle is typically given as: (x − h)2 (y − k)2 = r2 (5.1.1) in this equation, the point (h, k) represents the center of the circle and r represents the radius of the circle. this equation is derived from the distance formula. the definition of a circle is the locus (or collection) of points that are equidistant from a. The equation of a circle is x^2 y^2=r^2, where r represents the radius, with a center at 0,0 and (x h)^2 (y k)^2=r^2, where r represents the radius, with a center at (h,k). the definition of a circle is a set of all points on a plane that are a fixed distance from a center. So, the equation of a circle is given by: (x−x1)2 (y−y1)2 = r2 (x − x 1) 2 (y − y 1) 2 = r 2. example: using the equation of circle formula, find the center and radius of the circle whose equation is (x 1)2 (y 2)2 = 9. solution: we will use the circle equation to determine the center and radius of the circle.
The Equation Of A Circle With Center 1 2 And Radius 4 Is Tessshebaylo The equation of a circle is x^2 y^2=r^2, where r represents the radius, with a center at 0,0 and (x h)^2 (y k)^2=r^2, where r represents the radius, with a center at (h,k). the definition of a circle is a set of all points on a plane that are a fixed distance from a center. So, the equation of a circle is given by: (x−x1)2 (y−y1)2 = r2 (x − x 1) 2 (y − y 1) 2 = r 2. example: using the equation of circle formula, find the center and radius of the circle whose equation is (x 1)2 (y 2)2 = 9. solution: we will use the circle equation to determine the center and radius of the circle. Since the radius of this this circle is 1, and its center is the origin, this picture's equation is. $$ (y 0)^2 (x 0)^2 = 1^2 \\ y^2 x^2 = 1 $$. Plot the center (a,b) 2. plot 4 points "radius" away from the center in the up, down, left and right direction. 3. sketch it in! example: plot (x−4) 2 (y−2) 2 = 25. the formula for a circle is (x−a)2 (y−b)2 = r2. so the center is at (4,2) and r2 is 25, so the radius is √25 = 5.
Comments are closed.