Difixample 5 If A Transversal Intersects Two Lines Such That The

By gudangdomain On Nov 7, 2024 Last updated

Example 5 If A Transversal Intersects Two Lines Such That Transcript. example 5 if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. in figure, transversal ad intersects two lines pq and rs at points b and c respectively. ray be is the bisector of bacq so , abe = ebq = 1 2 ( abq ) and ray cg is the. (iv) two lines parallel to the same line are to each other. (v) if a transversal intersects a pair of lines in such away that a pair of alternate angles are equal, then the lines are (vi) if a transversal intersects a pair of lines in such away that the sum of interior angles on the same side of transversal is 180°, then the lines are.

Difixample 5 If A Transversal Intersects Two Lines Such That The 1. identify the given information: we have two lines, pq and rs, intersected by a transversal ad. the bisectors of a pair of corresponding angles, be and cg, are given to be parallel. 2. label the angles: let angle abq be one of the corresponding angles formed by the transversal ad and line pq. let angle bcg be the corresponding angle formed by. Thus, the sum of the interior angles on the same side of the line p and between the lines l and m is 180 ∘. therefore, l and m are parallel. hence, if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then the two lines are parallel. Study with quizlet and memorize flashcards containing terms like select all that apply. which of the following statements are true of a transversal? it is a line. it is parallel to other coplanar lines. it intersects two or more coplanar lines. it bisects line segments. it can never be perpendicular to other lines., given l||m and m∠1 = 60°, select all angles that are also equal to 60°. 2. Two nonadjacent angles formed by two lines and a transversal such that the angles lie on opposite sides of the transversal and are not between the two lines corresponding angles two nonadjacent angles formed by two lines and a transversal such that the angles are on the same side of the transversal, one interior and one exterior.

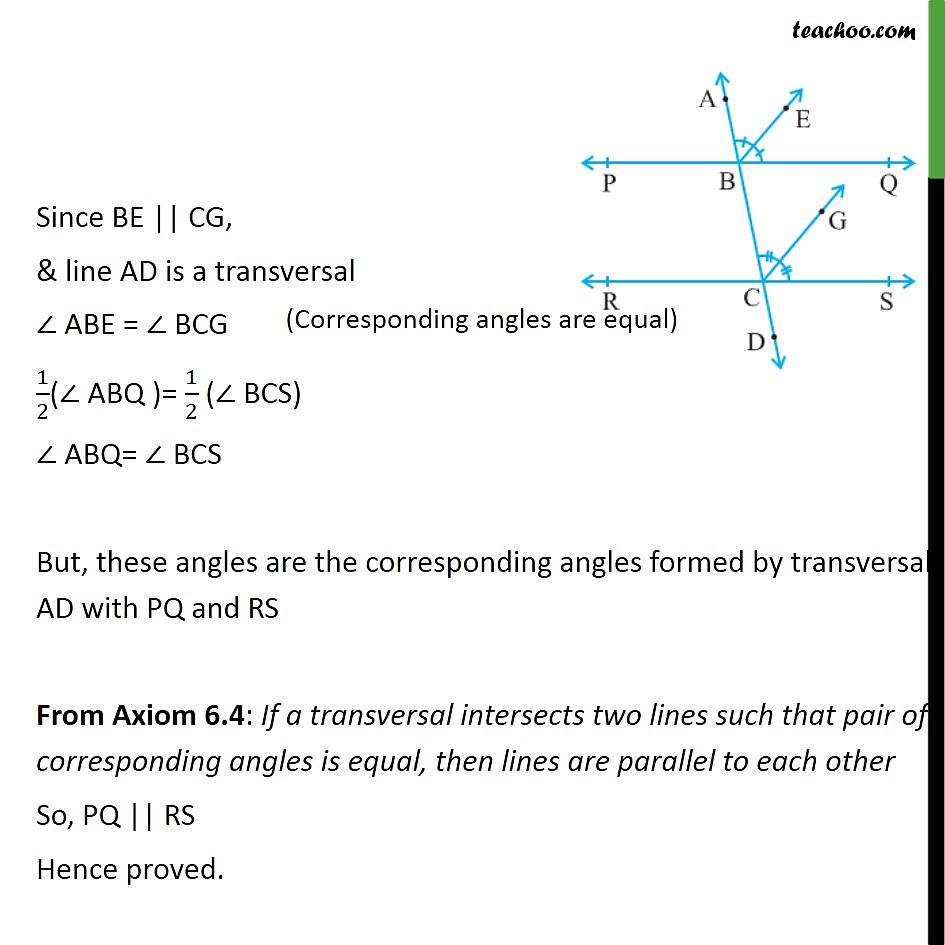
Example 5 If A Transversal Intersects Two Lines Such That Study with quizlet and memorize flashcards containing terms like select all that apply. which of the following statements are true of a transversal? it is a line. it is parallel to other coplanar lines. it intersects two or more coplanar lines. it bisects line segments. it can never be perpendicular to other lines., given l||m and m∠1 = 60°, select all angles that are also equal to 60°. 2. Two nonadjacent angles formed by two lines and a transversal such that the angles lie on opposite sides of the transversal and are not between the two lines corresponding angles two nonadjacent angles formed by two lines and a transversal such that the angles are on the same side of the transversal, one interior and one exterior. Now use the converse of the corresponding angle theorem to prove two lines parallel. complete step by step answer: here we have to prove that if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. let us represent this situation diagrammatically. A transversal is defined as a line that passes through two lines in the same plane at two distinct points in the geometry. a transversal intersection with two lines produces various types of angles in pairs, such as consecutive interior angles, corresponding angles and alternate angles. a transversal produces 8 angles and this can be observed.

Difixample 5 If A Transversal Intersects Two Lines Such That The Now use the converse of the corresponding angle theorem to prove two lines parallel. complete step by step answer: here we have to prove that if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. let us represent this situation diagrammatically. A transversal is defined as a line that passes through two lines in the same plane at two distinct points in the geometry. a transversal intersection with two lines produces various types of angles in pairs, such as consecutive interior angles, corresponding angles and alternate angles. a transversal produces 8 angles and this can be observed.

If A Transversal Intersects A Pair Of Lines In Such A Way That A Pair

Get ready to delve into a myriad of Difixample 5 If A Transversal Intersects Two Lines Such That The-related content that will ignite your curiosity, deepen your understanding, and perhaps even spark a newfound passion. Our goal is to be your go-to resource for all things Difixample 5 If A Transversal Intersects Two Lines Such That The, providing you with articles, insights, and discussions that cater to your every interest and question.

If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are

If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are Class 9th maths Chapter 6 Lines and angles Example 5 | If a transversal intersects two lines such If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are If a transversal intersects two lines such that the bisectors of a pair of corresponding angles ... Ms. W. Lesson: Angle Relationships when a Transversal Intersects a Set of Parallel Lines If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are Parallel Lines cut by a Transversal If A Transversal Intersects Two Lines Such A Pair Of Corresponding Angles Is Equal Then The Two ... If a transversal intersects two lines in such a way that a pair of consecuitive interior angle If a transversal intersects two lines such that the bisectors of a pair of corresponding angles ... If A Transversal Intersects Two Lines Such That A Pair Of Alternate Interior Angles Is Equal .... 3.1 (5 of 5) Two Lines cut by a Transversal.mp4 If A Transversal Intersects Two Lines Such That A Pair Of Interior Angles On The Same Side Of ... Theorem 6.5 : If a transversal intersects two lines such that a pair of interior angles on the s... Example5|Lines and angles|NCERT|If a transversal inter…..then prove that the two lines are parallel. Simplify: 3)(44) transversal intersects two lines such that the bisectors of pair of corresponding … Parallel Lines, Transversals, and Vertical Angles Parallel and Perpendicular Lines, Transversals, Alternate Interior Angles, Alternate Exterior Angles If a transversal intersects two lines,the bisectors of a pair of Corresponding angles are llal, . If two lines are intersected by a transversal in such a way that the bisectors of a pair of corr...

Conclusion

Upon a thorough analysis, one can see that this specific piece gives worthwhile awareness about Difixample 5 If A Transversal Intersects Two Lines Such That The. From start to finish, the journalist shows substantial skill concerning the matter. Specifically, the portion covering this feature stands out as a key takeaway. Furthermore, the publication is noteworthy in disentangling complex concepts in an user-friendly manner. What’s more, the reporter includes actual cases that improve the relatability. A supplementary feature that makes this publication unique is the in-depth research of an array of aspects related to Difixample 5 If A Transversal Intersects Two Lines Such That The. The scribes methodical style certifies that spectators gain a well-rounded understanding of the subject matter. Thanks for this post. Should you have any questions, please go ahead and contact me by means of comments or email. I am interested in hearing from you. In finishing up, to delve deeper, here are a handful of pertinent publications that are likely informative:May you find them engaging!