Deriving The Mean And Variance Of The Least Squares Slope Estimator In

Deriving The Mean And Variance Of The Least Squares Slope Estimator In I derive the mean and variance of the sampling distribution of the slope estimator (beta 1 hat) in simple linear regression (in the fixed x case). i discuss. The variance of a random variable x is defined as the expected value of the square of the deviation of different values of x from the mean x̅. it shows how spread the distribution of a random.

Deriving The Least Squares Regression Estimators Youtube That is, the least squares estimate of the slope is our old friend the plug in estimate of the slope, and thus the least squares intercept is also the plug in intercept. going forward the equivalence between the plug in estimator and the least squares estimator is a bit of a special case for linear models. in some non linear. The first step consists of dividing both sides by − 2. the second step follows by breaking up the sum into three separate sums over yi, β0 and β1xi. the third step comes from moving the sums over xi and yi to the other side of the equation. the final step comes from dividing though by n and applying our definition of ˉx and ˉy. In the simple linear regression case y = β0 β1x, you can derive the least square estimator ˆβ1 = ∑ (xi − ˉx) (yi − ˉy) ∑ (xi − ˉx)2 such that you don't have to know ˆβ0 to estimate ˆβ1. suppose i have y = β1x1 β2x2, how do i derive ˆβ1 without estimating ˆβ2? or is this not possible? regression. multiple regression. Derivation of ols estimator in class we set up the minimization problem that is the starting point for deriving the formulas for the ols intercept and slope coe cient. that problem was, min ^ 0; ^ 1 xn i=1 (y i ^ 0 ^ 1x i)2: (1) as we learned in calculus, a univariate optimization involves taking the derivative and setting equal to 0.

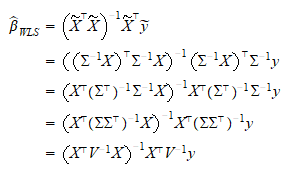
Least Squares Estimate Formula In the simple linear regression case y = β0 β1x, you can derive the least square estimator ˆβ1 = ∑ (xi − ˉx) (yi − ˉy) ∑ (xi − ˉx)2 such that you don't have to know ˆβ0 to estimate ˆβ1. suppose i have y = β1x1 β2x2, how do i derive ˆβ1 without estimating ˆβ2? or is this not possible? regression. multiple regression. Derivation of ols estimator in class we set up the minimization problem that is the starting point for deriving the formulas for the ols intercept and slope coe cient. that problem was, min ^ 0; ^ 1 xn i=1 (y i ^ 0 ^ 1x i)2: (1) as we learned in calculus, a univariate optimization involves taking the derivative and setting equal to 0. Least squares estimate, unless s2 x = 0, i.e., unless the sample variance of xis zero, i.e., unless all the x ihave the same value. (obviously, with only one value of the xcoordinate, we can’t work out the slope of a line!) moreover, if s2 x >0, then there is exactly one combination of slope and intercept which minimizes the mse in sample. 7.3 least squares: the theory. now that we have the idea of least squares behind us, let's make the method more practical by finding a formula for the intercept a 1 and slope b. we learned that in order to find the least squares regression line, we need to minimize the sum of the squared prediction errors, that is: q = ∑ i = 1 n (y i − y.