Derivatives The Easy Way In Calculus

Derivative Rules Cheat Sheet Calculus Ace Tutors Blog It means that, for the function x 2, the slope or "rate of change" at any point is 2x. so when x=2 the slope is 2x = 4, as shown here: or when x=5 the slope is 2x = 10, and so on. note: f’ (x) can also be used to mean "the derivative of": f’ (x) = 2x. "the derivative of f (x) equals 2x". or simply "f dash of x equals 2x". The tangent line will be horizontal when its slope is zero, that is, the derivative is zero. setting the derivative equal to zero gives: 3x 2 6x 24 = 0 or x 2 2x 8 = 0 or (x 4)(x 2) = 0 so that x = 4 or x = 2.

Calculus Derivative Rules Video Lessons Examples Solutions Differential calculus 6 units · 117 skills. unit 1 limits and continuity. unit 2 derivatives: definition and basic rules. unit 3 derivatives: chain rule and other advanced topics. unit 4 applications of derivatives. unit 5 analyzing functions. unit 6 parametric equations, polar coordinates, and vector valued functions. course challenge. Derivatives of all six trig functions are given and we show the derivation of the derivative of sin(x) sin. . (x) and tan(x) tan (x). derivatives of exponential and logarithm functions – in this section we derive the formulas for the derivatives of the exponential and logarithm functions. derivatives of inverse trig functions – in this. The derivative tells us the slope of a function at any point. there are rules we can follow to find many derivatives. for example: the slope of a constant value (like 3) is always 0; the slope of a line like 2x is 2, or 3x is 3 etc; and so on. here are useful rules to help you work out the derivatives of many functions (with examples below). 3.3.3 use the product rule for finding the derivative of a product of functions. 3.3.4 use the quotient rule for finding the derivative of a quotient of functions. 3.3.5 extend the power rule to functions with negative exponents. 3.3.6 combine the differentiation rules to find the derivative of a polynomial or rational function.

Derivatives For Beginners Basic Introduction Youtube The derivative tells us the slope of a function at any point. there are rules we can follow to find many derivatives. for example: the slope of a constant value (like 3) is always 0; the slope of a line like 2x is 2, or 3x is 3 etc; and so on. here are useful rules to help you work out the derivatives of many functions (with examples below). 3.3.3 use the product rule for finding the derivative of a product of functions. 3.3.4 use the quotient rule for finding the derivative of a quotient of functions. 3.3.5 extend the power rule to functions with negative exponents. 3.3.6 combine the differentiation rules to find the derivative of a polynomial or rational function. Worked example: derivative of cos³ (x) using the chain rule. worked example: derivative of ln (√x) using the chain rule. worked example: derivative of √ (3x² x) using the chain rule. chain rule overview. worked example: chain rule with table. quotient rule from product & chain rules. chain rule with the power rule. This calculus 1 video tutorial provides a basic introduction into derivatives. full 1 hour 35 minute video: patreon mathsciencetutor.
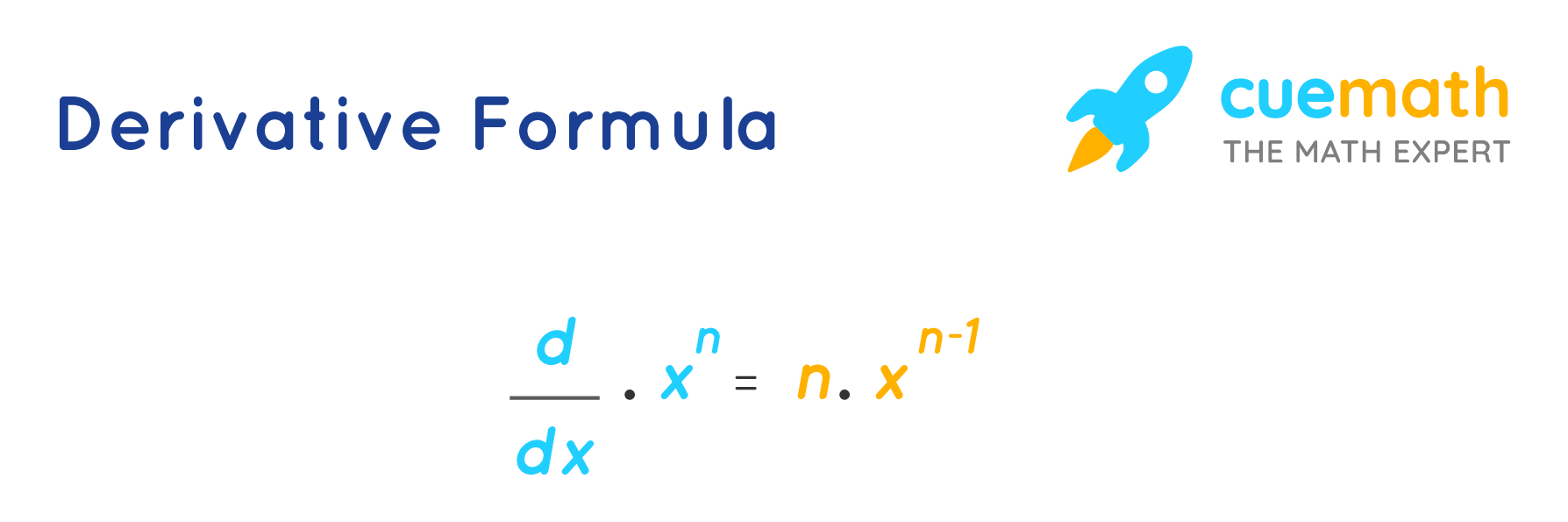
Derivative Formula Learn Formula To Find Derivatives Worked example: derivative of cos³ (x) using the chain rule. worked example: derivative of ln (√x) using the chain rule. worked example: derivative of √ (3x² x) using the chain rule. chain rule overview. worked example: chain rule with table. quotient rule from product & chain rules. chain rule with the power rule. This calculus 1 video tutorial provides a basic introduction into derivatives. full 1 hour 35 minute video: patreon mathsciencetutor.

Calculus Basic Derivative Rules Youtube

Comments are closed.