Derivatives Of Functions Maths Shorts Differentiation Derivatives Logarithm Exponential

Calculus Exponential Derivatives Examples Solutions Videos Derivative of the exponential function. just as when we found the derivatives of other functions, we can find the derivatives of exponential and logarithmic functions using formulas. as we develop these formulas, we need to make certain basic assumptions. the proofs that these assumptions hold are beyond the scope of this course. The function e(x) = ex is called the natural exponential function. its inverse, l(x) = logex = lnx is called the natural logarithmic function. figure 3.33 the graph of e(x) = ex is between y = 2x and y = 3x. for a better estimate of e, we may construct a table of estimates of b ′ (0) for functions of the form b(x) = bx.

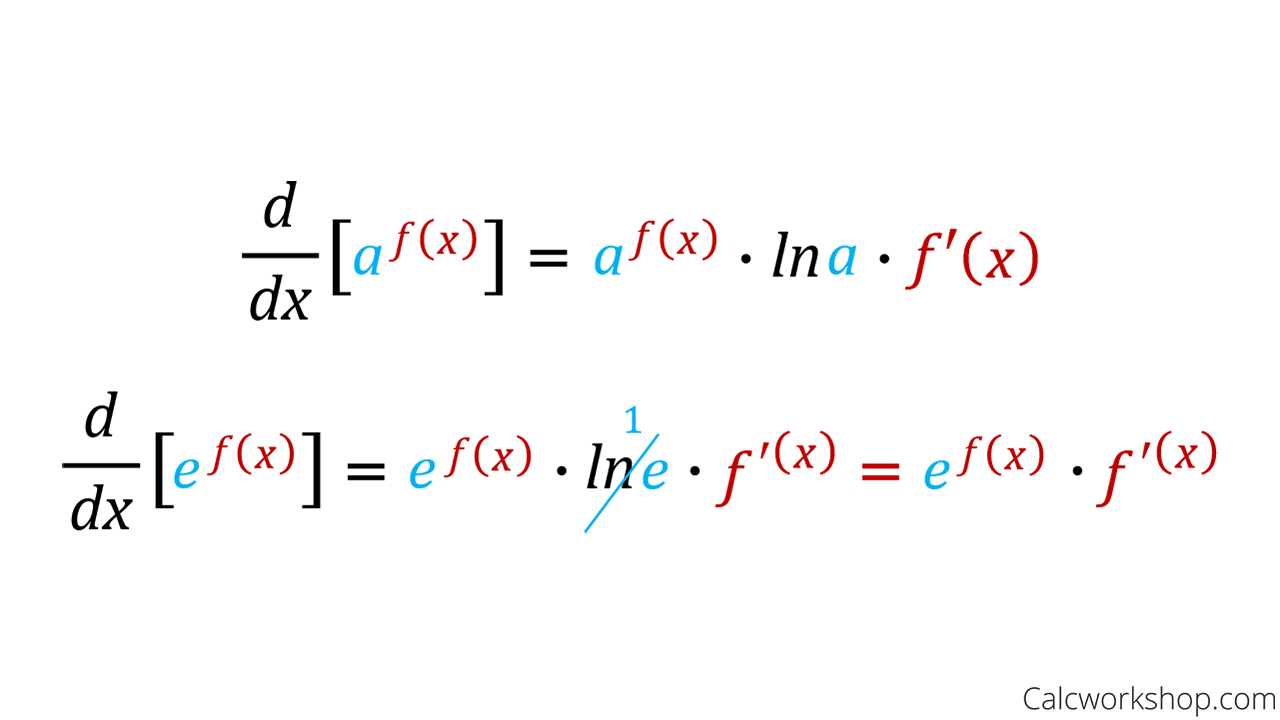
Derivative Of Exponential Function Ln. ⁡. (z) is increasing or decreasing at the following points. z = 1 z = 1. z =5 z = 5. z = 20 z = 20. solution. here is a set of practice problems to accompany the derivatives of exponential and logarithm functions section of the derivatives chapter of the notes for paul dawkins calculus i course at lamar university. These functions require a technique called logarithmic differentiation, which allows us to differentiate any function of the form \(h(x)=g(x)^{f(x)}\). it can also be used to convert a very complex differentiation problem into a simpler one, such as finding the derivative of \(y=\frac{x\sqrt{2x 1}}{e^x\sin ^3x}\). Derivative of the exponential function. just as when we found the derivatives of other functions, we can find the derivatives of exponential and logarithmic functions using formulas. as we develop these formulas, we need to make certain basic assumptions. the proofs that these assumptions hold are beyond the scope of this course. Find the derivative of logarithmic functions. use logarithmic differentiation to determine the derivative of a function. so far, we have learned how to differentiate a variety of functions, including trigonometric, inverse, and implicit functions. in this section, we explore derivatives of exponential and logarithmic functions.

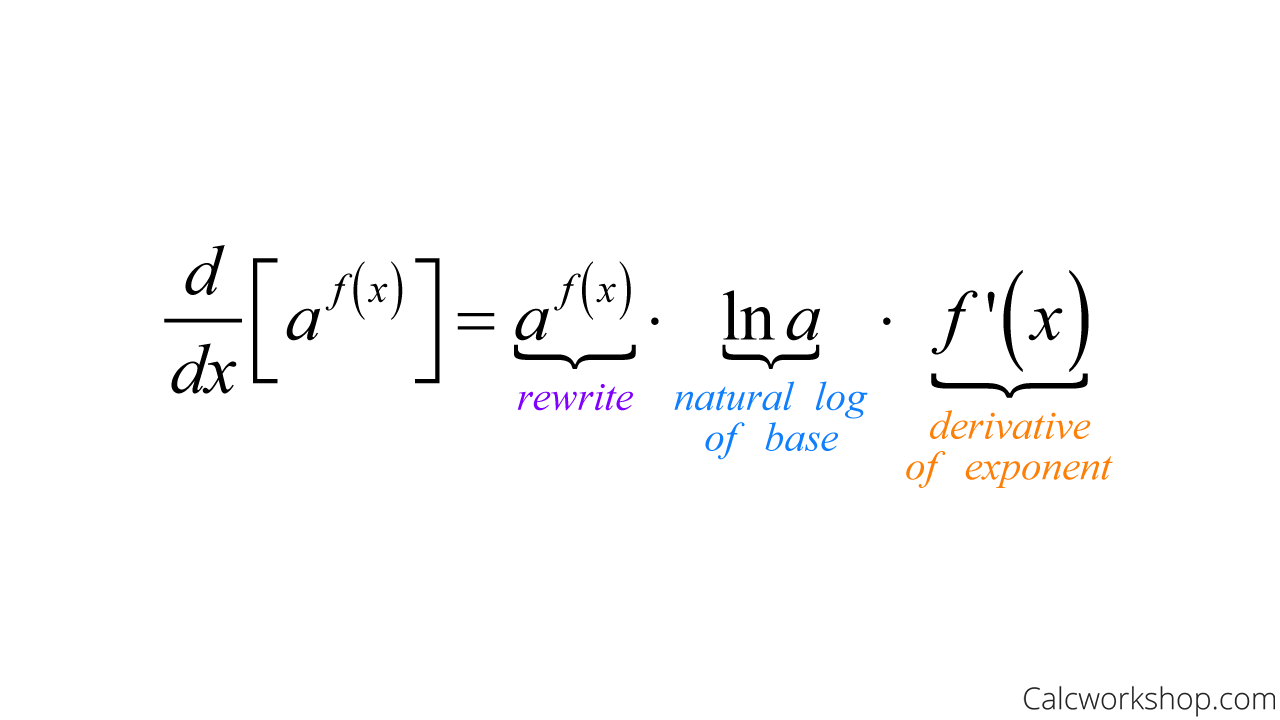
Derivative Of Exponential Functions Derivative of the exponential function. just as when we found the derivatives of other functions, we can find the derivatives of exponential and logarithmic functions using formulas. as we develop these formulas, we need to make certain basic assumptions. the proofs that these assumptions hold are beyond the scope of this course. Find the derivative of logarithmic functions. use logarithmic differentiation to determine the derivative of a function. so far, we have learned how to differentiate a variety of functions, including trigonometric, inverse, and implicit functions. in this section, we explore derivatives of exponential and logarithmic functions. Note that we need to require that x> 0 x> 0 since this is required for the logarithm and so must also be required for its derivative. it can also be shown that, d dx (ln|x|) = 1 x x ≠ 0 d d x (ln | x |) = 1 x x ≠ 0. using this all we need to avoid is x = 0 x = 0. in this case, unlike the exponential function case, we can actually find the. Just as when we found the derivatives of other functions, we can find the derivatives of exponential and logarithmic functions using formulas. we know that 2.7182 <e <2.7183. the graph of e (x) = e x together with the line y = x 1 are shown in figure 3.138. this line is tangent to the graph of e (x) = e x at x = 0.

Differentiation Formulas Rules Basic Trig Full List Teachoo Note that we need to require that x> 0 x> 0 since this is required for the logarithm and so must also be required for its derivative. it can also be shown that, d dx (ln|x|) = 1 x x ≠ 0 d d x (ln | x |) = 1 x x ≠ 0. using this all we need to avoid is x = 0 x = 0. in this case, unlike the exponential function case, we can actually find the. Just as when we found the derivatives of other functions, we can find the derivatives of exponential and logarithmic functions using formulas. we know that 2.7182 <e <2.7183. the graph of e (x) = e x together with the line y = x 1 are shown in figure 3.138. this line is tangent to the graph of e (x) = e x at x = 0.