Derivatives Of Composite Functions The Chain Rule
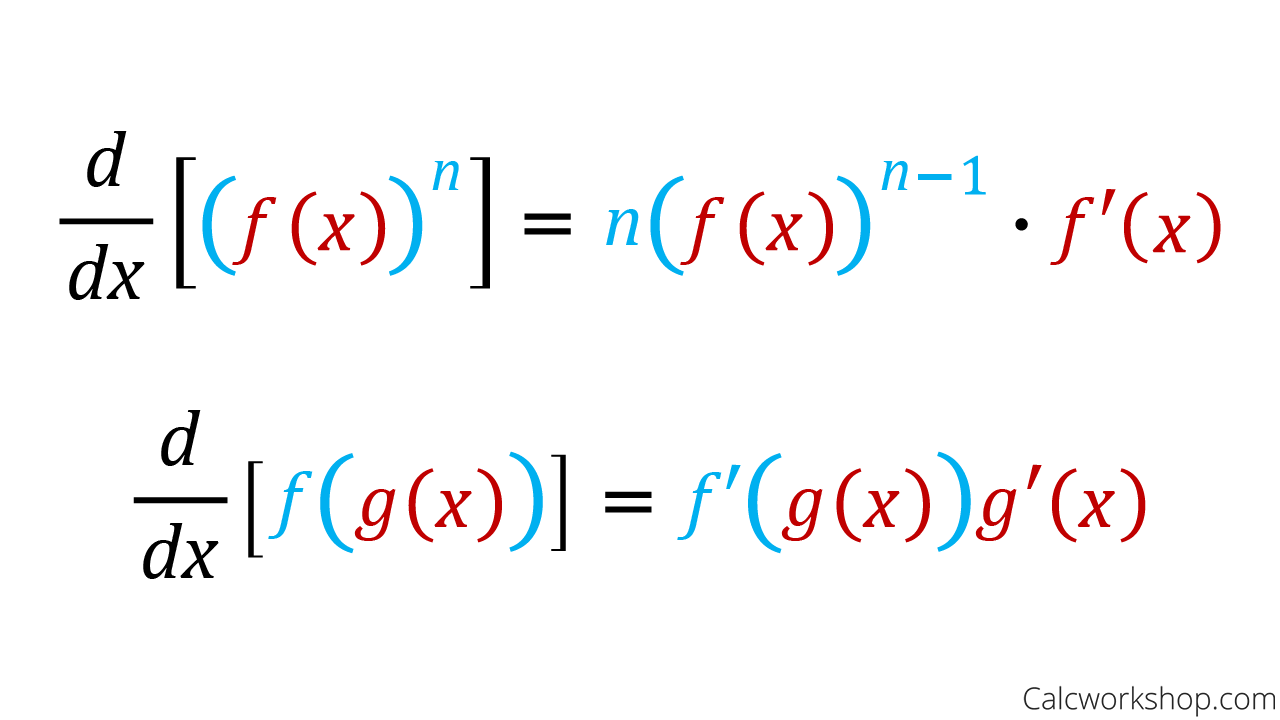
Chain Rule Explained W 7 Step By Step Examples However, using all of those techniques to break down a function into simpler parts that we are able to differentiate can get cumbersome. instead, we use the chain rule, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. T. e. in calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions f and g in terms of the derivatives of f and g. more precisely, if is the function such that for every x, then the chain rule is, in lagrange's notation, or, equivalently, the chain rule may also be expressed in.

Derivatives Of Composite Functions The Chain Rule Youtube Recall that the chain rule for the derivative of a composite of two functions can be written in the form \[\dfrac{d}{dx}\big(f(g(x))\big)=f′\big(g(x)\big)g′(x). \nonumber \] in this equation, both \(f(x)\) and \(g(x)\) are functions of one variable. now suppose that \(f\) is a function of two variables and \(g\) is a function of one variable. Derivatives of composite functions in one variable are determined using the simple chain rule formula. let us solve a few examples to understand the calculation of the derivatives: example 1: determine the derivative of the composite function h (x) = (x 3 7) 10. solution: now, let u = x 3 7 = g (x), here h (x) can be written as h (x) = f (g. The chain rule is used to calculate the derivative of a composite function. the chain rule formula states that dy dx = dy du × du dx . in words, differentiate the outer function while keeping the inner function the same then multiply this by the derivative of the inner function. Recognize the composition: first we found the outer and inner functions f and g. find the derivatives we need: then we found the derivatives of f and g. plug into the formula: next, we put f '() and g '(x) into the chain rule formula. make sure the inner function is re substituted: finally, we plugged in g(x) for the in f'.
Differentiating Composite Functions Using The Chain Rule Calculus The chain rule is used to calculate the derivative of a composite function. the chain rule formula states that dy dx = dy du × du dx . in words, differentiate the outer function while keeping the inner function the same then multiply this by the derivative of the inner function. Recognize the composition: first we found the outer and inner functions f and g. find the derivatives we need: then we found the derivatives of f and g. plug into the formula: next, we put f '() and g '(x) into the chain rule formula. make sure the inner function is re substituted: finally, we plugged in g(x) for the in f'. This chain rule is also known as the outside inside rule or the composite function rule or function of a function rule. it is used only to find the derivatives of the composite functions. the theorem of chain rule: let f be a real valued function that is a composite of two functions g and h. i.e, f = g o h. suppose u = h(x), where du dx and dg. The chain rule is used to differentiate composite functions. specifically, it allows us to use differentiation rules on more complicated functions by differentiating the inner function and outer function separately. intuitively, oftentimes a function will have another function "inside" it that is first related to the input variable. since we know the derivative of a function is the.

Comments are closed.