Derivatives Of Composite Functions Chain Rule Product Quotient Rule

Derivatives Of Composite Functions Chain Rule Product Quotient State the chain rule for the composition of two functions. apply the chain rule together with the power rule. apply the chain rule and the product quotient rules correctly in combination when both are necessary. recognize the chain rule for a composition of three or more functions. describe the proof of the chain rule. This calculus video tutorial explains how to find the derivative of composite functions using the chain rule. it also covers a few examples and practice pro.

Differentiation Product Rule Quotient Rule Chain Rule And Covered basic differentiation? great! now let's take things to the next level. in this topic, you will learn general rules that tell us how to differentiate products of functions, quotients of functions, and composite functions. anxious to find the derivative of eˣ⋅sin(x²)? you've come to the right place. State the chain rule for the composition of two functions. apply the chain rule together with the power rule. apply the chain rule and the product quotient rules correctly in combination when both are necessary. recognize the chain rule for a composition of three or more functions. describe the proof of the chain rule. Worked example. let’s now take a look at a problem to see the chain rule in action as we find the derivative of the following function: chain rule — examples. see, all we did was first take the derivative of the outside function (parentheses), keeping the inside as is. next, we multiplied by the derivative of the inside function, and lastly. Rule: the chain rule. let f and g be functions. for all x in the domain of g for which g is differentiable at x and f is differentiable at g (x), the derivative of the composite function. h ′ (x) = f ′ (g (x)) g ′ (x). alternatively, if y is a function of u, and u is a function of x, then. d y d x = d y d u ⋅ d u d x.
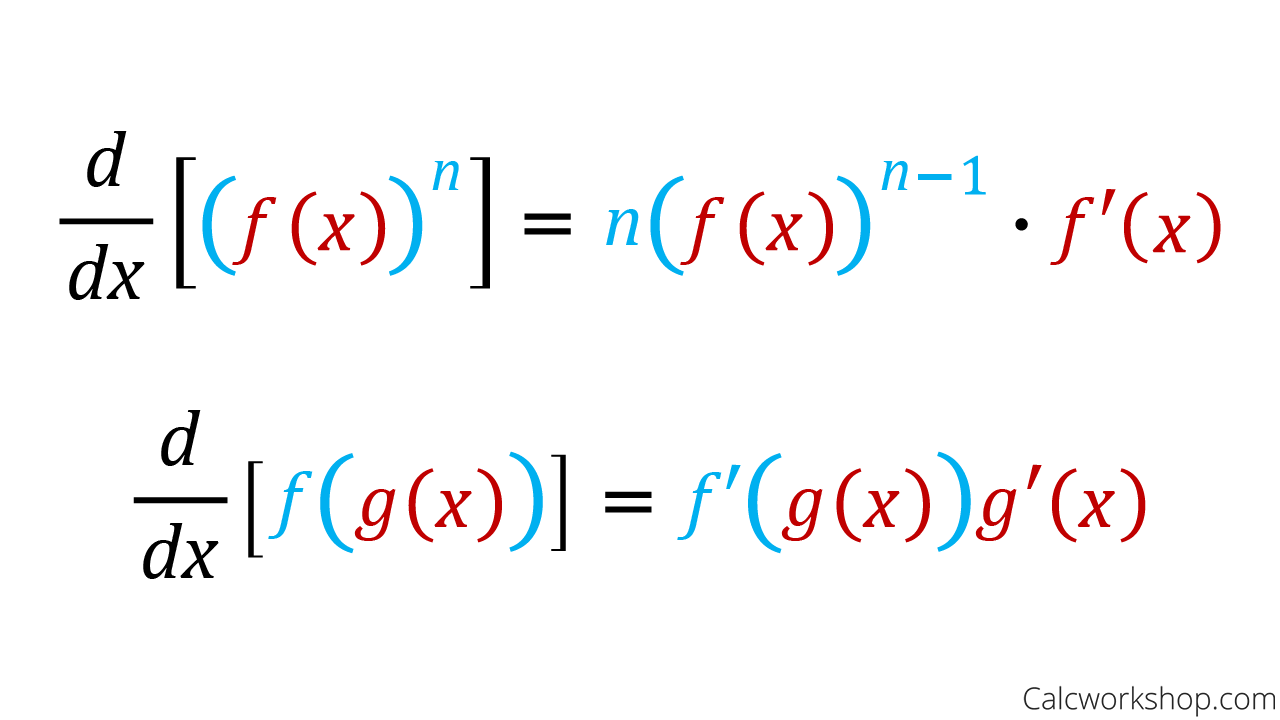
Chain Rule Explained W 7 Step By Step Examples Worked example. let’s now take a look at a problem to see the chain rule in action as we find the derivative of the following function: chain rule — examples. see, all we did was first take the derivative of the outside function (parentheses), keeping the inside as is. next, we multiplied by the derivative of the inside function, and lastly. Rule: the chain rule. let f and g be functions. for all x in the domain of g for which g is differentiable at x and f is differentiable at g (x), the derivative of the composite function. h ′ (x) = f ′ (g (x)) g ′ (x). alternatively, if y is a function of u, and u is a function of x, then. d y d x = d y d u ⋅ d u d x. The chain rule if f and g are functions that have derivatives, then the composite function h 1x 2 f1g 1x 22has a derivative given by h ¿1x 2 f¿1g 1x 22g ¿1x 2. chapter 2 99 in words, the chain rule says, the derivative of a composite function is the product of the derivative of the outer function evaluated at the inner function and. Objectives. state the chain rule for the composition of two functions. apply the chain rule together with the power rule. apply the chain rule and the product quotient rules correctly in combination when both are necessary. recognize the chain rule for a composition of three or more functions. describe the proof of the chain rule.

Chain Product And Quotient Rule Worksheet The chain rule if f and g are functions that have derivatives, then the composite function h 1x 2 f1g 1x 22has a derivative given by h ¿1x 2 f¿1g 1x 22g ¿1x 2. chapter 2 99 in words, the chain rule says, the derivative of a composite function is the product of the derivative of the outer function evaluated at the inner function and. Objectives. state the chain rule for the composition of two functions. apply the chain rule together with the power rule. apply the chain rule and the product quotient rules correctly in combination when both are necessary. recognize the chain rule for a composition of three or more functions. describe the proof of the chain rule.

Comments are closed.