Derivatives From A Graphical And Numerical Approach Chowdhury Docx

By gudangdomain On Nov 8, 2024 Last updated

Derivatives From A Graphical And Numerical Approach Chowdhury Docx Understanding the derivative from a graphical and numerical approach so far, our understanding of the derivative is that it represents the slope of the tangent line drawn to a curve at a point. View derivatives from a graphical and numerical approach chowdhury.docx from mth 263 at northern virginia community college. derivatives from a graphical and numerical approach practice use the graph ai homework help.

Understanding The Derivative From A Graphical And Numerical Approach Welcome to my channel miftah math lessons!in this lesson, i explained how to find derivatives from graphs. since the derivative represents the slope of the t. Limits calculate limits algebraically example. average rate of change. animation: 10.4 average rates of change. average rate of change quadratic equation example. average rate of change 3 by x example. derivatives graphical and numerical viewpoints. animation: 10.5 derivatives numerical and graphical viewpoints. A simple approximation of the ﬁrst derivative is f0(x) ≈ f(x h)−f(x) h, (5.1) where we assume that h > 0. what do we mean when we say that the expression on the right hand side of (5.1) is an approximation of the derivative? for linear functions (5.1) is actually an exact expression for the derivative. for almost all other functions,. Derivative function. if fis a function, its derivative functionf'is the function whose value f'(x) at xis the derivative of fat x. its domain is the set of all xat which fis differentiable. equivalently, f'associates to each xthe slope of the tangent to the graph of the function fat x, or the instantaneous rate of change of fat x. thus,.

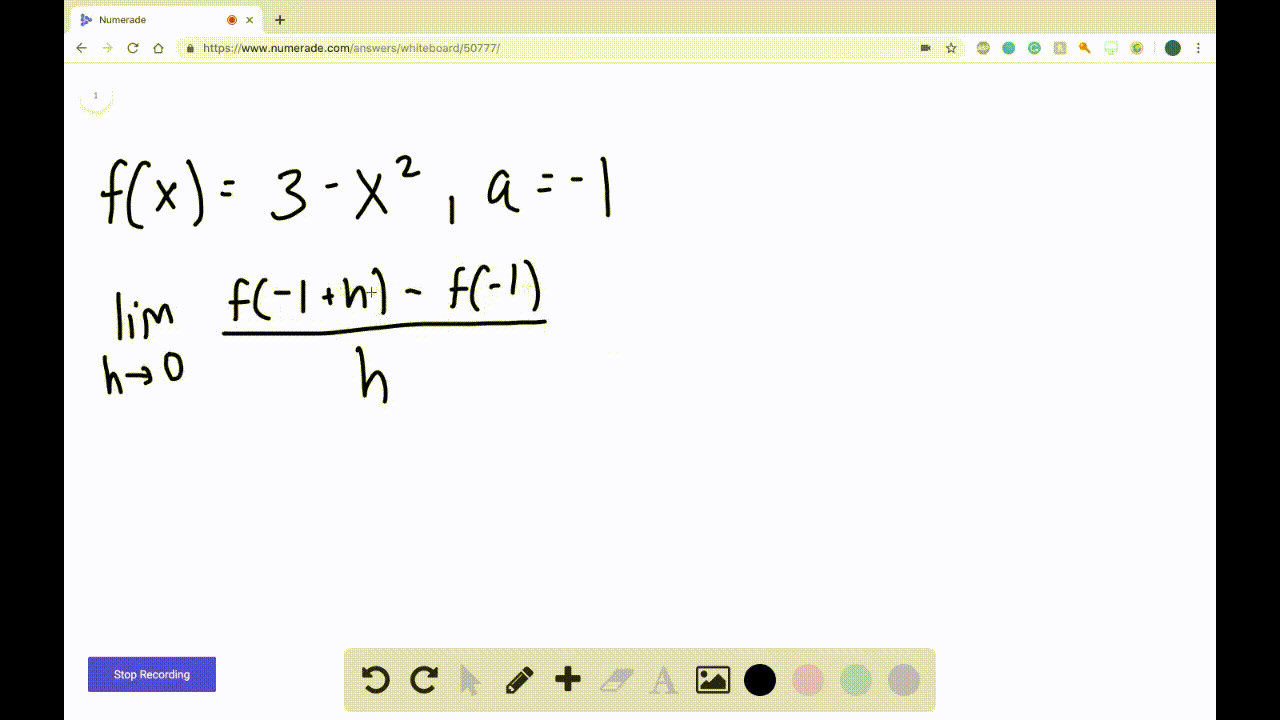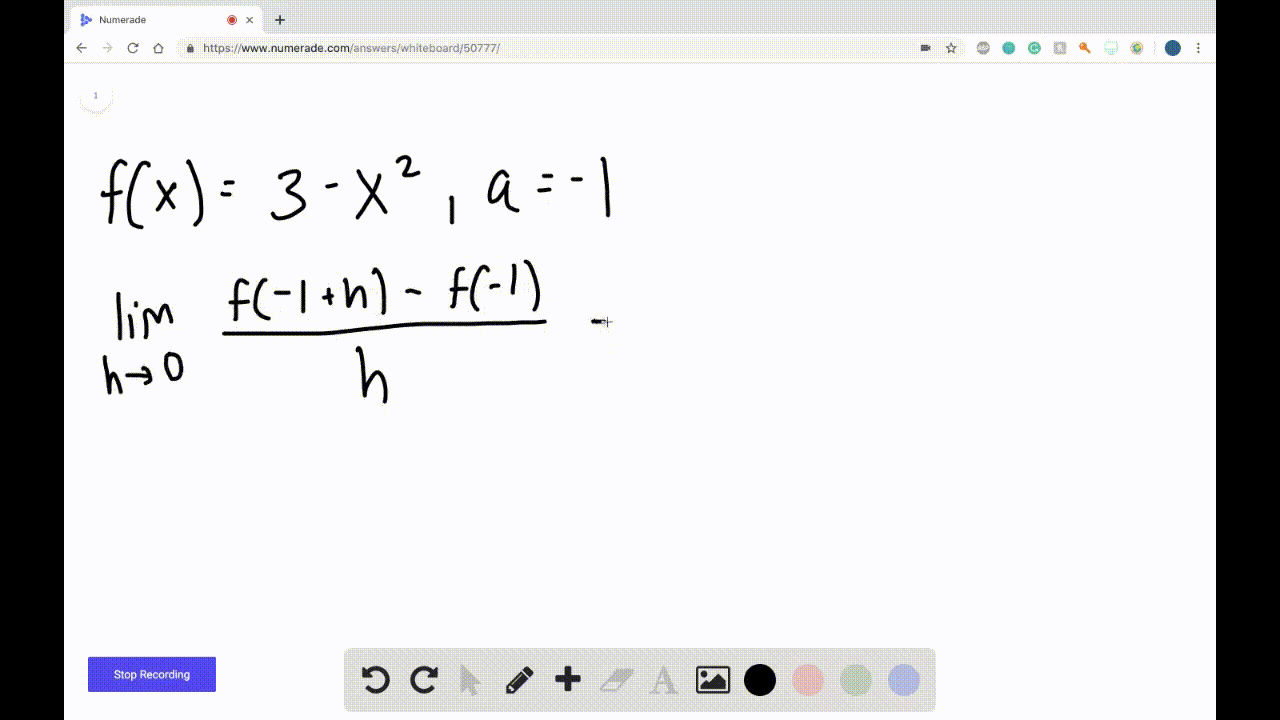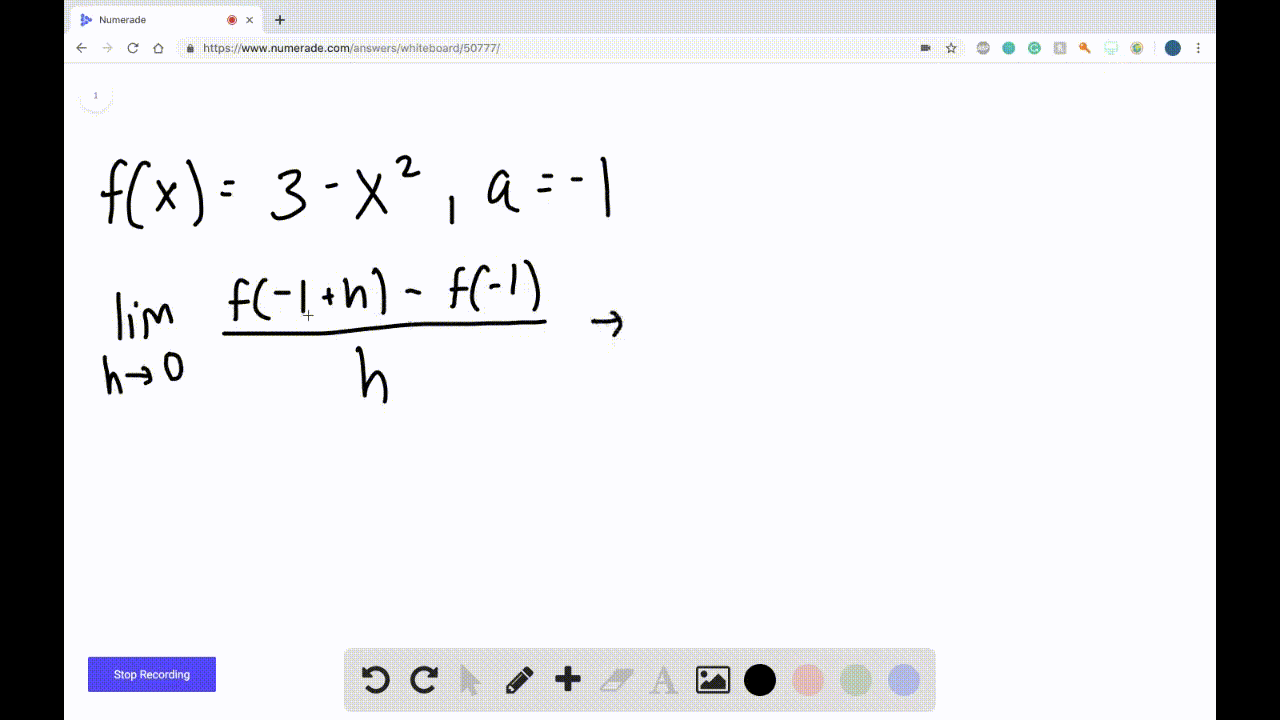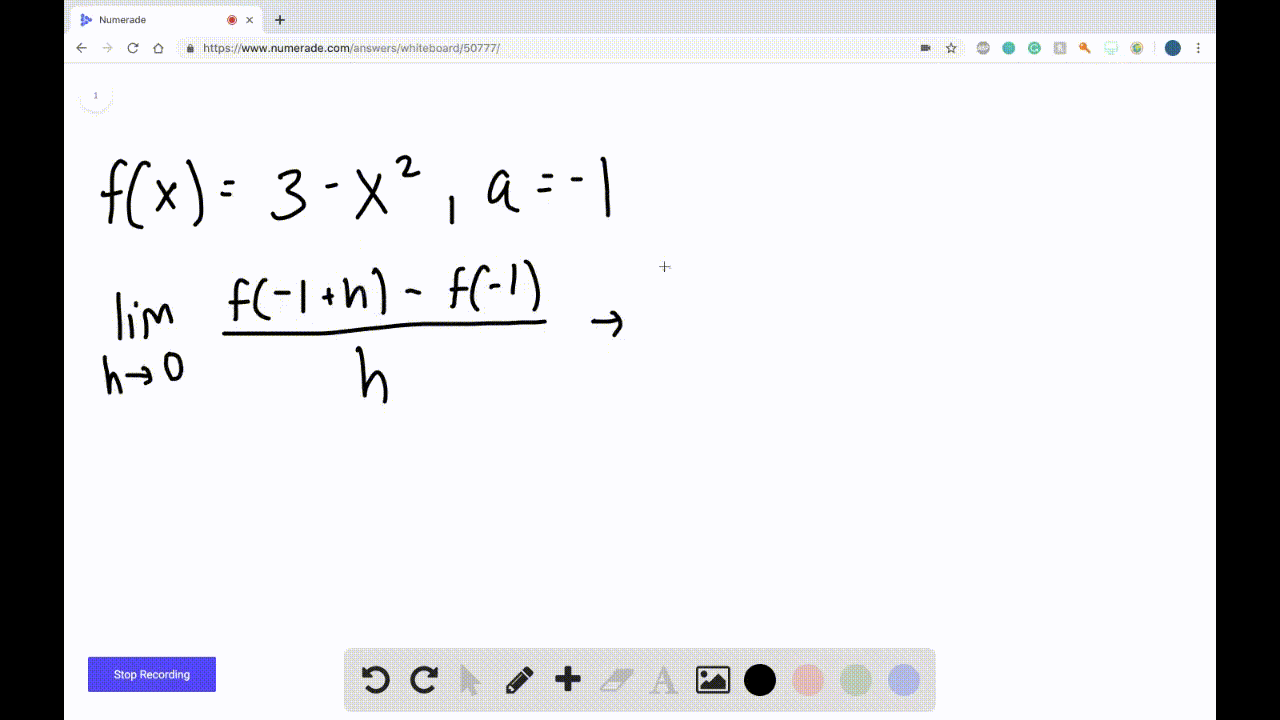
Derivatives Calculus Graphical Numerical Alg A simple approximation of the ﬁrst derivative is f0(x) ≈ f(x h)−f(x) h, (5.1) where we assume that h > 0. what do we mean when we say that the expression on the right hand side of (5.1) is an approximation of the derivative? for linear functions (5.1) is actually an exact expression for the derivative. for almost all other functions,. Derivative function. if fis a function, its derivative functionf'is the function whose value f'(x) at xis the derivative of fat x. its domain is the set of all xat which fis differentiable. equivalently, f'associates to each xthe slope of the tangent to the graph of the function fat x, or the instantaneous rate of change of fat x. thus,. Determining the graph of a derivative of a function. suppose a function is f (x)=x^3 12x 3 f (x) = x3 −12x 3 and its graph is as follows: forget the equation for a moment and just look at the graph. now, to find the graph of {f}' f ′ from the above graph, we have to find two kinds of very important points. Numerical differentiation. use of numerical analysis to estimate derivatives of functions. finite difference estimation of derivative. in numerical analysis, numerical differentiation algorithms estimate the derivative of a mathematical function or function subroutine using values of the function and perhaps other knowledge about the function.

Calculus Graphical Numerical Algebraic 3rd Edition Answers Ch 4 Determining the graph of a derivative of a function. suppose a function is f (x)=x^3 12x 3 f (x) = x3 −12x 3 and its graph is as follows: forget the equation for a moment and just look at the graph. now, to find the graph of {f}' f ′ from the above graph, we have to find two kinds of very important points. Numerical differentiation. use of numerical analysis to estimate derivatives of functions. finite difference estimation of derivative. in numerical analysis, numerical differentiation algorithms estimate the derivative of a mathematical function or function subroutine using values of the function and perhaps other knowledge about the function.

Calculus Graphical Numerical Algebraic 3rd Edition Answers Ch 4

Journey through the realms of imagination and storytelling, where words have the power to transport, inspire, and transform. Join us as we dive into the enchanting world of literature, sharing literary masterpieces, thought-provoking analyses, and the joy of losing oneself in the pages of a great book in our Derivatives From A Graphical And Numerical Approach Chowdhury Docx section.

Finding derivatives from a graph

Finding derivatives from a graph Given fx sketch the first and second derivative graph Sketching Derivatives From Parent Functions - f f' f'' Graphs - f(x), Calculus Derivatives from Graphs Sketching a Derivative from the Graph of a Function Sketching Derivatives From Graphs Solution: Derivatives from Graphs Calculus - Estimate the derivative of a function from the graph Graphs from Derivatives, Part 1 Exponential derivative visual Determining Derivatives from Graphs (1 of 3: Identifying major features) Animation: The graph of a function and it's 1st and 2nd Derivative Definition of the Derivative Graph the Derivative Function Given the Graph of a Quadratic Function Derivatives the Easy Way in Calculus Calculus 180 Derivatives from the Graph of a Function Calculus 1: How Derivatives Affect the Shape of a Graph (Section 4.3) | Math with Professor V Graph the Derivative Function Given the Graph of a Degree 4 Function How to Graph the Derivative of a Function Using Only ITS Graph! EASY PROCESS😉 Math with Professor V Product and Quotient Rule | Finding Derivatives from given Graphs of functions | Calculus

Conclusion

After exploring the topic in depth, it can be concluded that piece provides pertinent understanding in connection with Derivatives From A Graphical And Numerical Approach Chowdhury Docx. Across the whole article, the commentator depicts a deep understanding in the field. Particularly, the review of this element stands out as a significant highlight. To add to that, the content shines in illustrating complex concepts in an clear manner. Additionally, the blogger includes illustrative examples that heighten the understanding. Another aspect that differentiates this write-up is the thorough investigation of several aspects related to Derivatives From A Graphical And Numerical Approach Chowdhury Docx. The creators scrupulous manner affirms that observers gain a well-rounded understanding of the subject matter. Thanks for your attention to this text. If you would like to know more, dont think twice to reach out to me utilizing the comments. I am eager to your comments. In conclusion, as you continue exploring, noted below are several akin pieces of content that are potentially worthwhile:Happy learning!