Derivatives Definition Of A Derivative Differentials Rules For

Derivative Rules What Are Differentiation Rules Examples To better understand the sequence in which the differentiation rules are applied, we use leibniz notation throughout the solution: f′ (x) = d dx(2x5 7) = d dx(2x5) d dx(7) apply the sum rule. = 2 d dx(x5) d dx(7) apply the constant multiple rule. = 2(5x4) 0 apply the power rule and the constant rule. = 10x4 simplify. The derivative f ′ (a) at a specific point x = a, being the slope of the tangent line to the curve at x = a, and. the derivative as a function, f ′ (x) as defined in definition 2.2.6. of course, if we have f ′ (x) then we can always recover the derivative at a specific point by substituting x = a.

Calculus Derivative Rules Formulas Examples Solutions Videos The derivative of a function describes the function's instantaneous rate of change at a certain point. another common interpretation is that the derivative gives us the slope of the line tangent to the function's graph at that point. learn how we define the derivative using limits. learn about a bunch of very useful rules (like the power, product, and quotient rules) that help us find. The derivative tells us the slope of a function at any point. there are rules we can follow to find many derivatives. for example: the slope of a constant value (like 3) is always 0; the slope of a line like 2x is 2, or 3x is 3 etc; and so on. here are useful rules to help you work out the derivatives of many functions (with examples below). Theorem 13 allows us to find the derivatives of a wide variety of functions. it can be used in conjunction with the power rule to find the derivatives of any polynomial. recall in example 36 that we found, using the limit definition, the derivative of \(f(x) = 3x^2 5x 7\). we can now find its derivative without expressly using limits:. 3.3.2 apply the sum and difference rules to combine derivatives. 3.3.3 use the product rule for finding the derivative of a product of functions. 3.3.4 use the quotient rule for finding the derivative of a quotient of functions. 3.3.5 extend the power rule to functions with negative exponents. 3.3.6 combine the differentiation rules to find the.

Derivative Rules Cheat Sheet Calculus Ace Tutors Blog Theorem 13 allows us to find the derivatives of a wide variety of functions. it can be used in conjunction with the power rule to find the derivatives of any polynomial. recall in example 36 that we found, using the limit definition, the derivative of \(f(x) = 3x^2 5x 7\). we can now find its derivative without expressly using limits:. 3.3.2 apply the sum and difference rules to combine derivatives. 3.3.3 use the product rule for finding the derivative of a product of functions. 3.3.4 use the quotient rule for finding the derivative of a quotient of functions. 3.3.5 extend the power rule to functions with negative exponents. 3.3.6 combine the differentiation rules to find the. Logarithmic differentiation is a technique which uses logarithms and its differentiation rules to simplify certain expressions before actually applying the derivative. [ citation needed ] logarithms can be used to remove exponents, convert products into sums, and convert division into subtraction — each of which may lead to a simplified. Combine the differentiation rules to find the derivative of a polynomial or rational function. finding derivatives of functions by using the definition of the derivative can be a lengthy and, for certain functions, a rather challenging process. for example, previously we found that [latex]\frac {d} {dx} (\sqrt {x})=\frac {1} {2\sqrt {x.
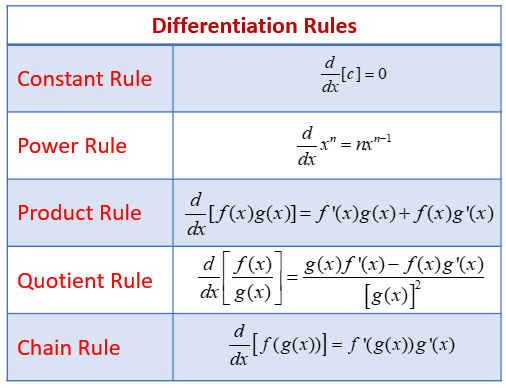
Examples Using The Derivative Rules With Formulas Videos Logarithmic differentiation is a technique which uses logarithms and its differentiation rules to simplify certain expressions before actually applying the derivative. [ citation needed ] logarithms can be used to remove exponents, convert products into sums, and convert division into subtraction — each of which may lead to a simplified. Combine the differentiation rules to find the derivative of a polynomial or rational function. finding derivatives of functions by using the definition of the derivative can be a lengthy and, for certain functions, a rather challenging process. for example, previously we found that [latex]\frac {d} {dx} (\sqrt {x})=\frac {1} {2\sqrt {x.

Derivative Formulas List Differentiation Formulas With Examples

Comments are closed.