Derivatives Calculus Graphical Numerical Alg

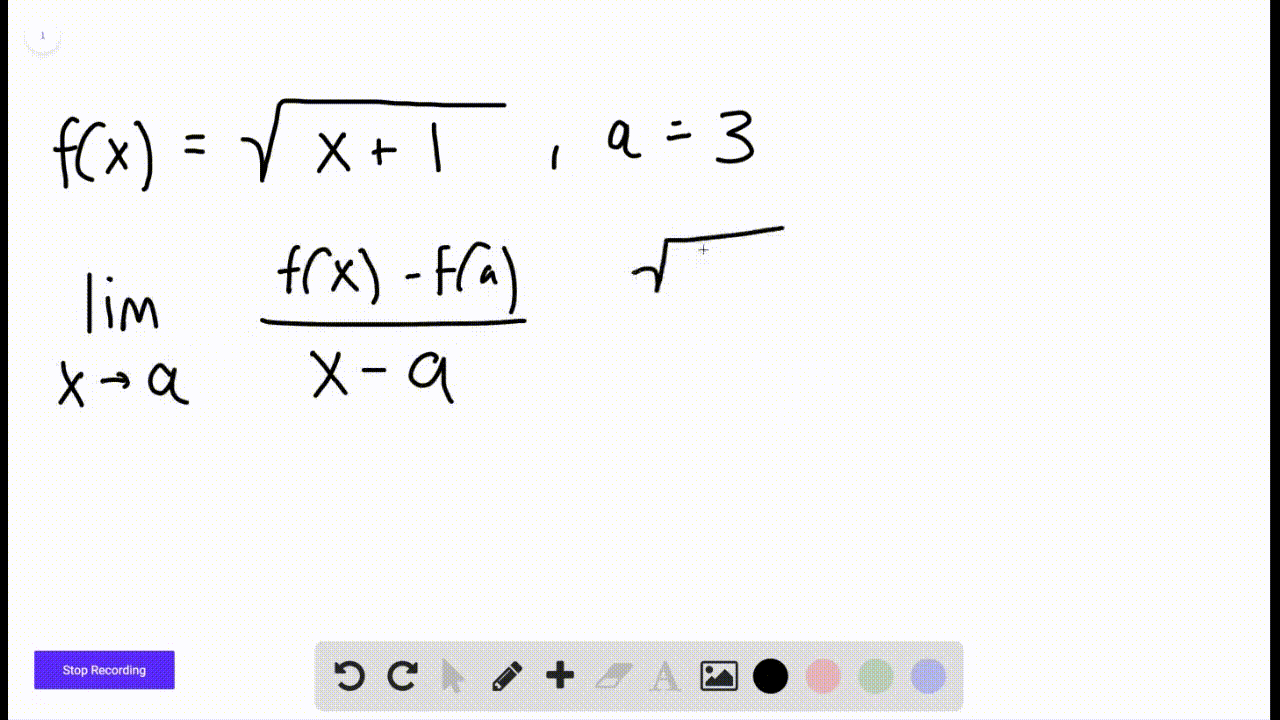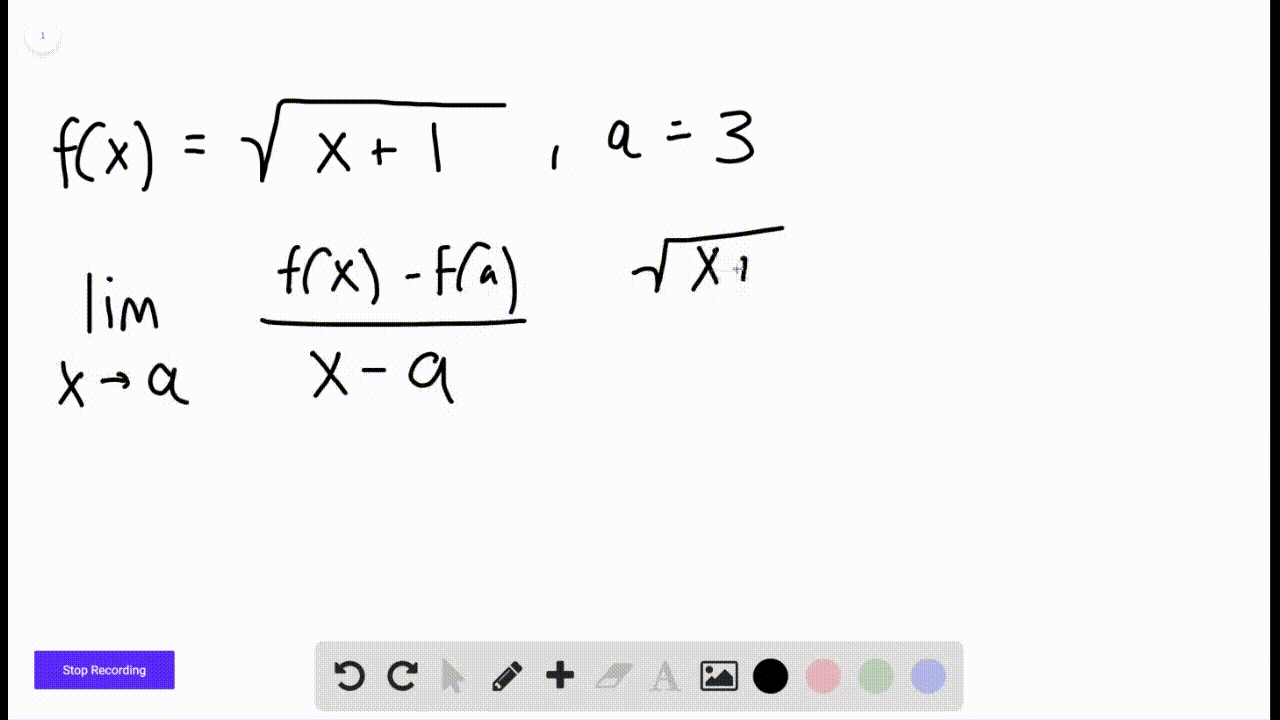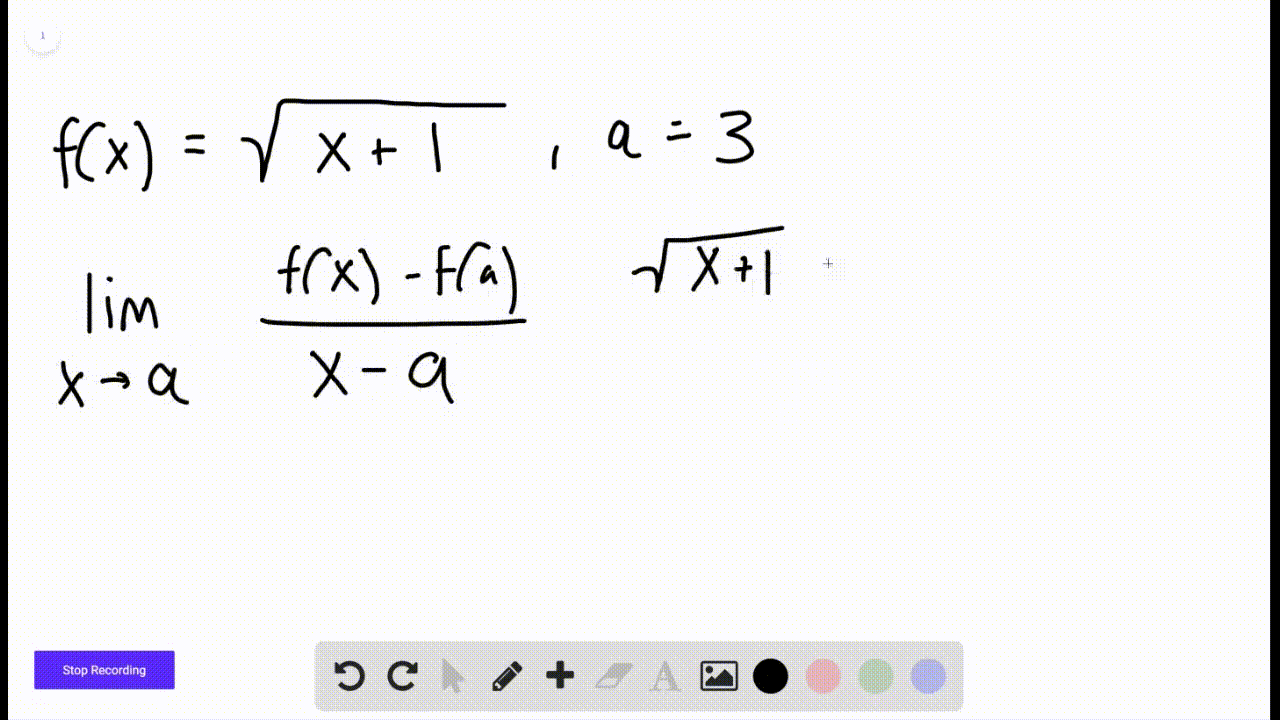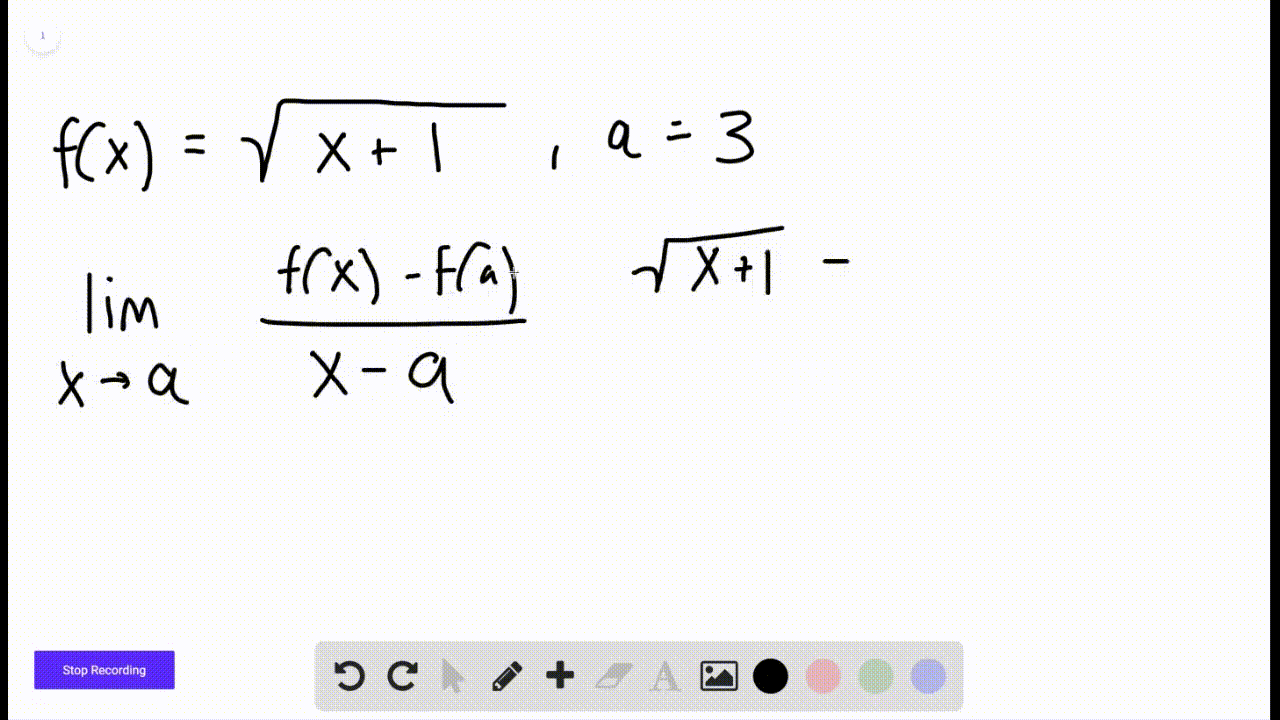
Derivatives Calculus Graphical Numerical Alg The derivative of a function describes the function's instantaneous rate of change at a certain point. another common interpretation is that the derivative gives us the slope of the line tangent to the function's graph at that point. learn how we define the derivative using limits. learn about a bunch of very useful rules (like the power, product, and quotient rules) that help us find. It means that, for the function x 2, the slope or "rate of change" at any point is 2x. so when x=2 the slope is 2x = 4, as shown here: or when x=5 the slope is 2x = 10, and so on. note: f’ (x) can also be used to mean "the derivative of": f’ (x) = 2x. "the derivative of f (x) equals 2x". or simply "f dash of x equals 2x".

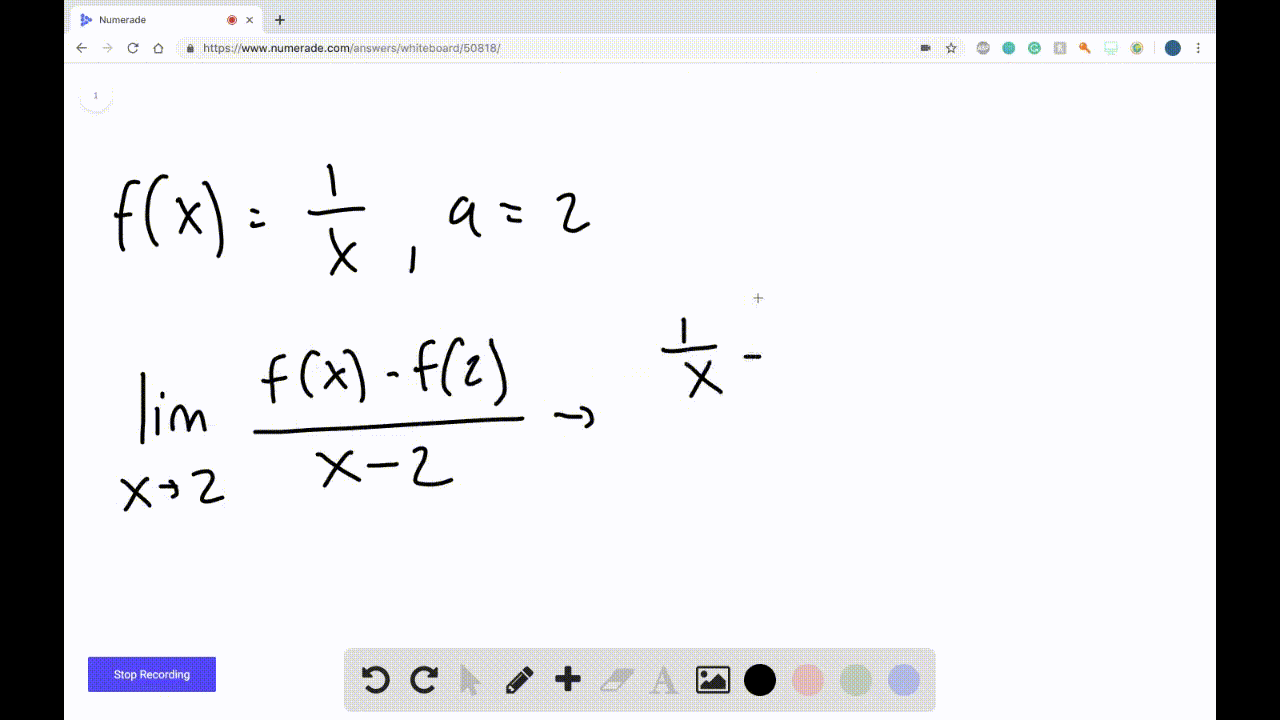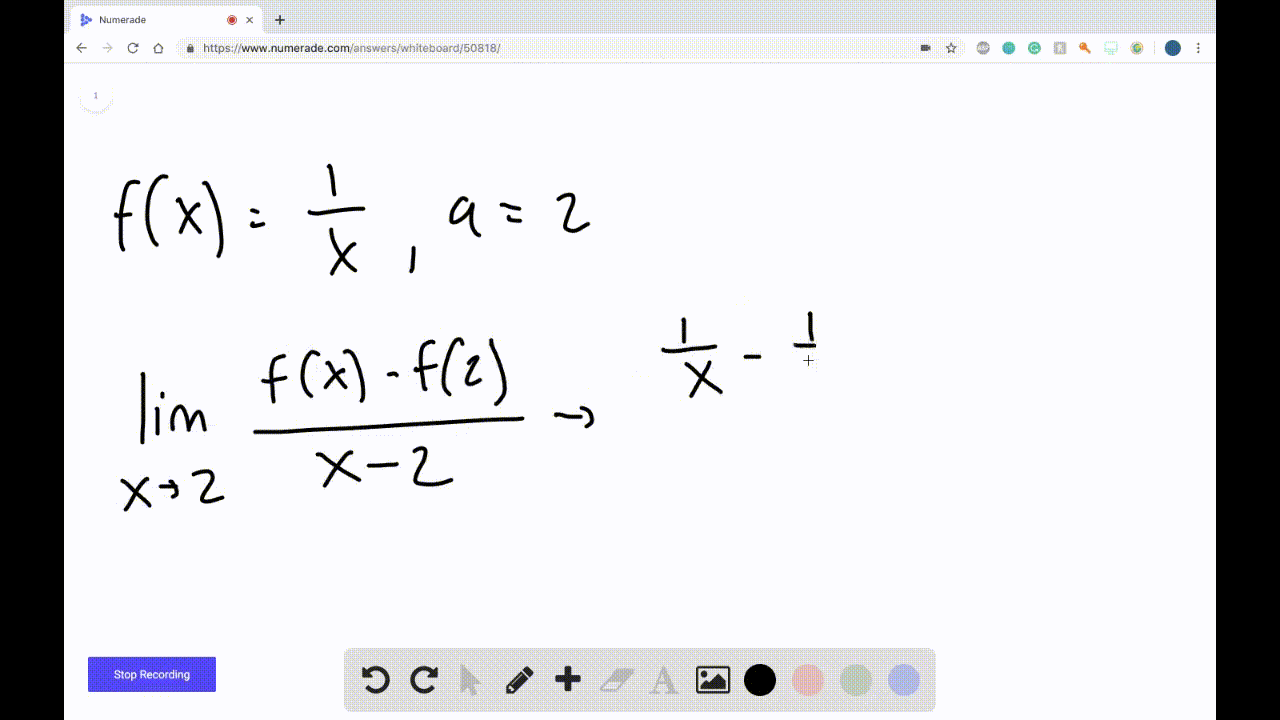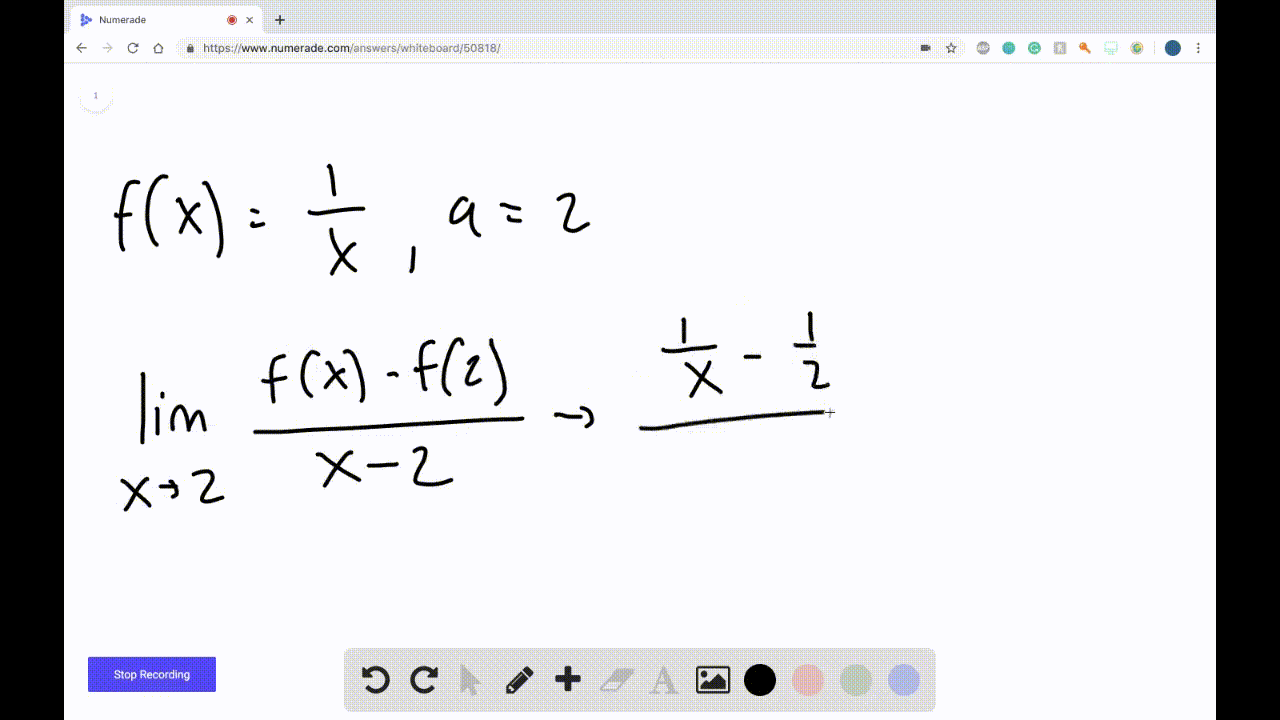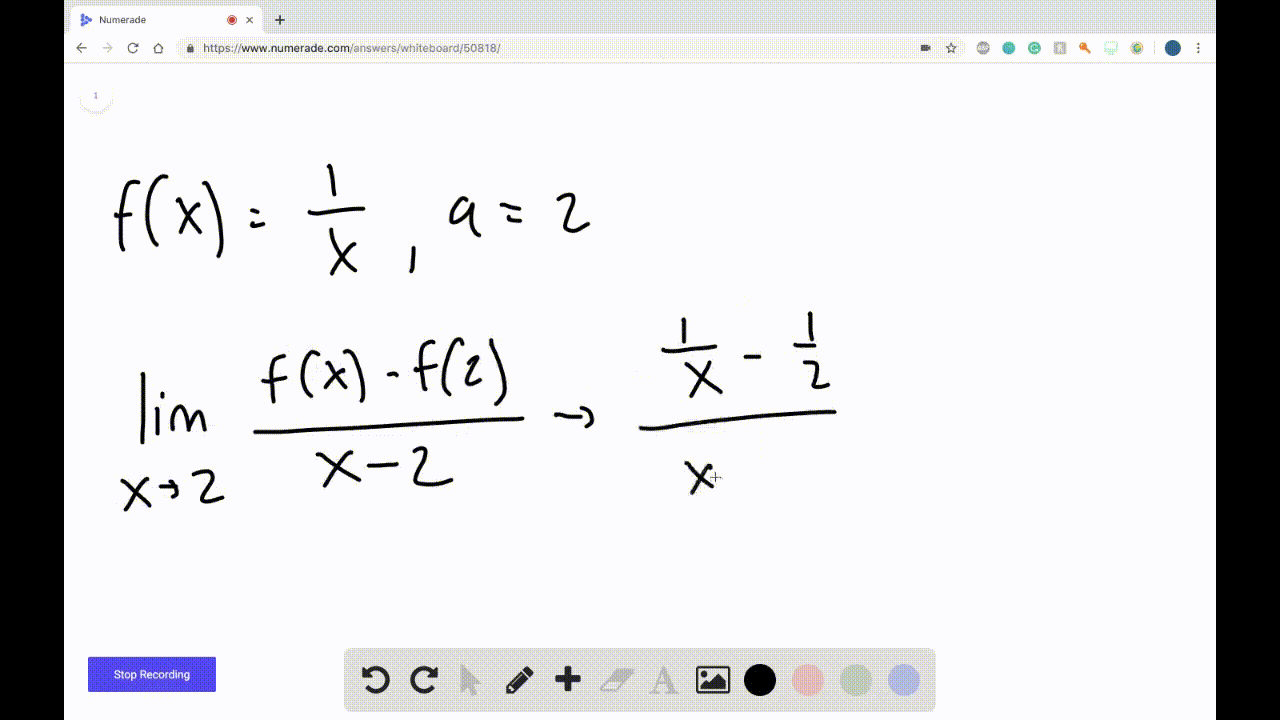
Derivatives Calculus Graphical Numerical Alg Derivatives of all six trig functions are given and we show the derivation of the derivative of sin(x) sin. ⁡. (x) and tan(x) tan (x). derivatives of exponential and logarithm functions – in this section we derive the formulas for the derivatives of the exponential and logarithm functions. derivatives of inverse trig functions – in this. Unit 2 differentiation: definition and fundamental properties 2.1 defining average and instantaneous rate of change at a point 2.2 defining the derivative of a function and using derivative notation (2.2 includes equation of the tangent line) 2.3 estimating derivatives of a function at a point 2.4 connecting differentiability and continuity. • work with functions represented in a variety of ways: graphical, numerical, analytical, or verbal. they should understand the connections among these representations. • understand the meaning of the derivative in terms of a rate of change and local linear approximation and they should be able to use derivatives to solve a variety of problems. Here's a hint: undefined is not used in calculus! this page titled 2.2: the limit of a function a numerical and graphical investigation (lecture notes for augmented lecture) is shared under a cc by nc sa 3.0 license and was authored, remixed, and or curated by roy simpson .

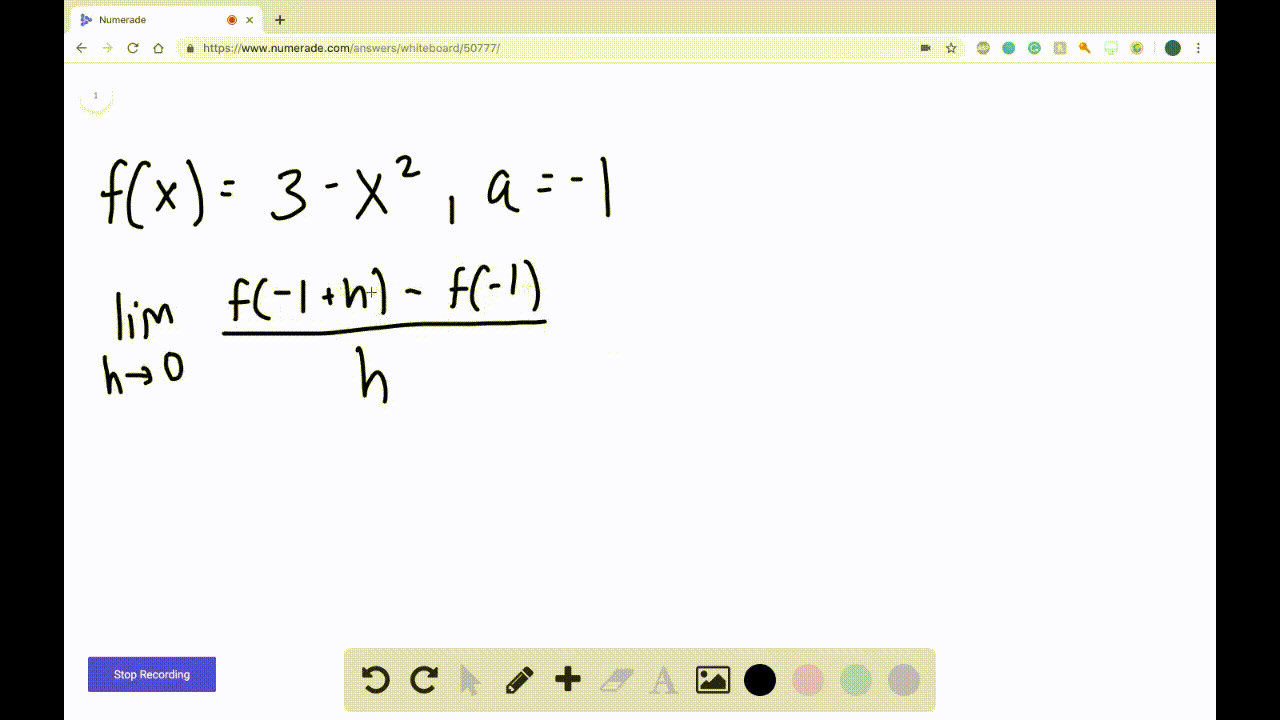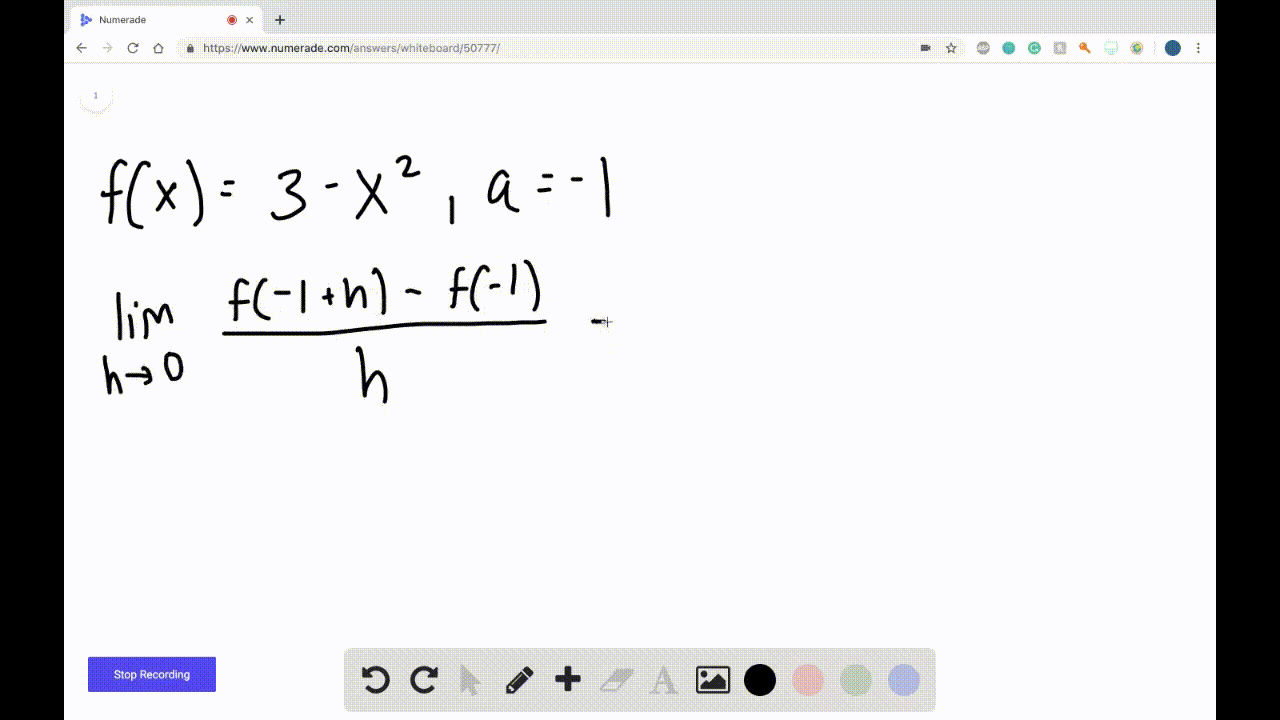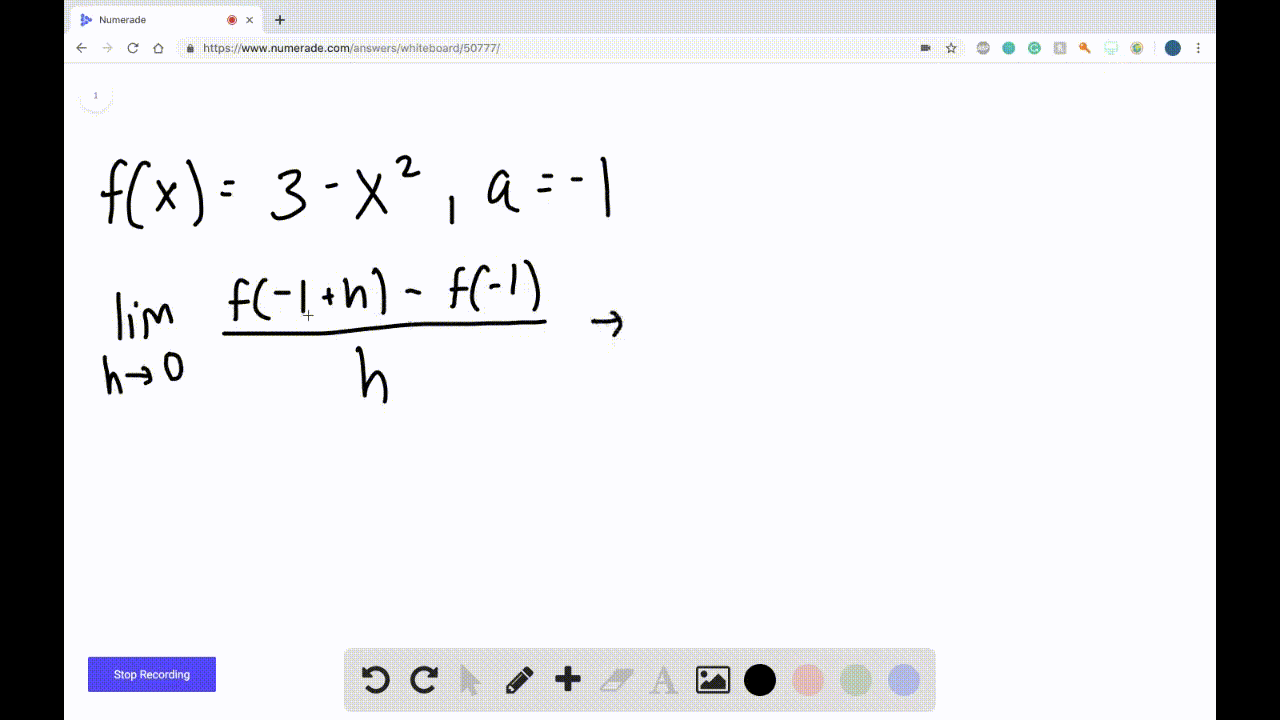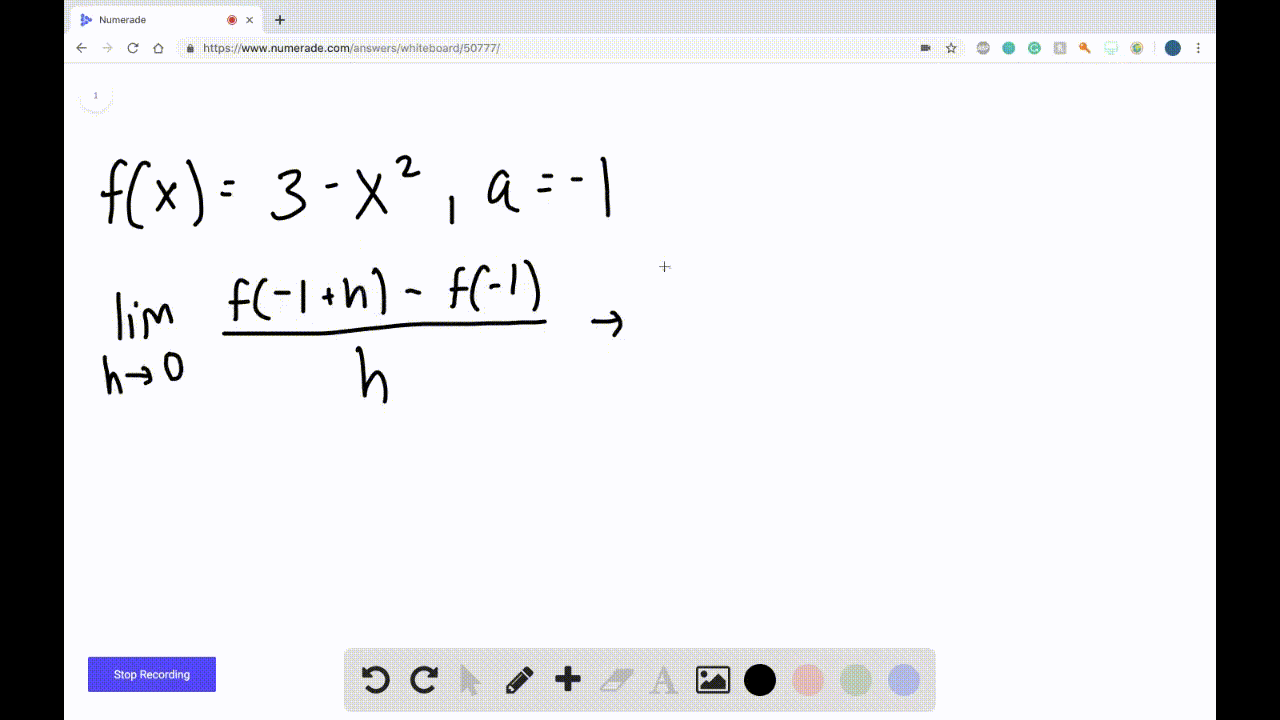
Derivatives Calculus Graphical Numerical Alg • work with functions represented in a variety of ways: graphical, numerical, analytical, or verbal. they should understand the connections among these representations. • understand the meaning of the derivative in terms of a rate of change and local linear approximation and they should be able to use derivatives to solve a variety of problems. Here's a hint: undefined is not used in calculus! this page titled 2.2: the limit of a function a numerical and graphical investigation (lecture notes for augmented lecture) is shared under a cc by nc sa 3.0 license and was authored, remixed, and or curated by roy simpson . Calculus: graphical, numerical, algebraic, ap edition 5th edition • isbn: 9780133311617 bert k waits, daniel kennedy, david m. bressoud, franklin demana, ross l. finney. 10.2 statistics (graphical) 10.3 statistics (numerical) 10.4 random variables and probability models 10.5 statistical literacy. chapter 11 an introduction to calculus: 11.1 limits and motion: the tangent problem 11.2 limits and motion: the area problem 11.3 more on limits 11.4 numerical derivatives and integrals. appendix a algebra review.

Calculus Graphical Numerical Algebraic 3rd Edition Chapter 4 Calculus: graphical, numerical, algebraic, ap edition 5th edition • isbn: 9780133311617 bert k waits, daniel kennedy, david m. bressoud, franklin demana, ross l. finney. 10.2 statistics (graphical) 10.3 statistics (numerical) 10.4 random variables and probability models 10.5 statistical literacy. chapter 11 an introduction to calculus: 11.1 limits and motion: the tangent problem 11.2 limits and motion: the area problem 11.3 more on limits 11.4 numerical derivatives and integrals. appendix a algebra review.