Derivative Of X Sinx Formula Proof X Sinx Derivative Imath

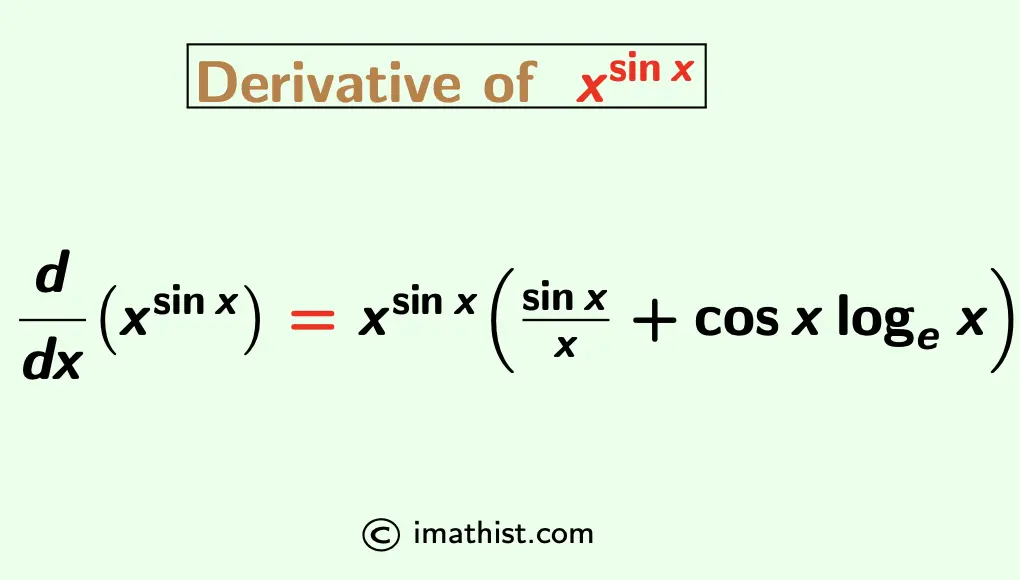
Derivative Of X Sinx Formula Proof X Sinx Derivative Imath Derivative of x sinx proof. question: prove that d dx(x sinx) = x sinx [sinx x cosx logx]. answer: let y=x sinx.we need to find dy dx. taking the natural logarithms both sides, we have. The following formulas will be proved by the definition of derivatives: 1. d d x (x n)=nx n 1. 2. d d x (e x)=e x. 3. d d x (a x) = a x log e a. 4. d d x (log x) = 1 x (x ≠ 0) 5. d d x (sin x) = cos x. 6. d d x (cos x) = sin x. 7. d d x (tan x) = sec 2 x.

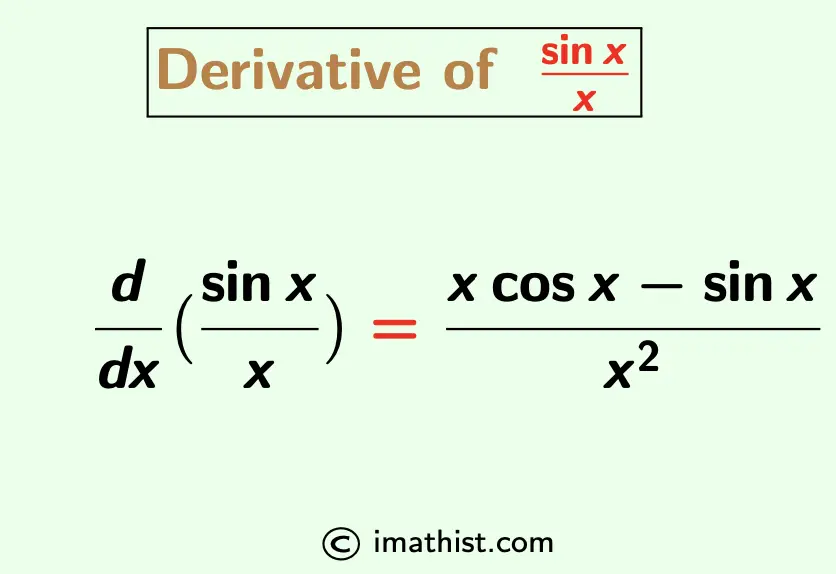
Derivative Of Sinx X Sinx X Derivative Imath We need to go back, right back to first principles, the basic formula for derivatives: dy dx = lim Δx→0 f (x Δx)−f (x) Δx. pop in sin (x): d dx sin (x) = lim Δx→0 sin (x Δx)−sin (x) Δx. we can then use this trigonometric identity: sin (a b) = sin (a)cos (b) cos (a)sin (b) to get: lim Δx→0 sin (x)cos (Δx) cos (x)sin (Δx. Key concepts. we can find the derivatives of sinx and cosx by using the definition of derivative and the limit formulas found earlier. the results are. d dx (sinx) = cosx and d dx (cosx) = − sinx. with these two formulas, we can determine the derivatives of all six basic trigonometric functions. In this video, we dive into the proof of the derivative of sin(x) using limit definition of the derivative, also known as the first principle. follow along a. Derivative of sin x, algebraic proof. a specific derivative formula tells us how to take the derivative of a specific function: if f(x) = xn then f (x) = nx n−1 . we’ll now compute a specific formula for the derivative of the function sin x. as before, we begin with the definition of the derivative: d sin(x Δx) − sin(x) sin x = lim dx.

Derivative Of Sin X Handout For 10th 12th Grade Lesson Planet In this video, we dive into the proof of the derivative of sin(x) using limit definition of the derivative, also known as the first principle. follow along a. Derivative of sin x, algebraic proof. a specific derivative formula tells us how to take the derivative of a specific function: if f(x) = xn then f (x) = nx n−1 . we’ll now compute a specific formula for the derivative of the function sin x. as before, we begin with the definition of the derivative: d sin(x Δx) − sin(x) sin x = lim dx. We’ll first use the definition of the derivative on the product. (fg)′ = lim h → 0f(x h)g(x h) − f(x)g(x) h. on the surface this appears to do nothing for us. we’ll first need to manipulate things a little to get the proof going. what we’ll do is subtract out and add in f(x h)g(x) to the numerator. We begin with the derivatives of the sine and cosine functions and then use them to obtain formulas for the derivatives of the remaining four trigonometric functions. calculating the derivatives of the sine and cosine functions will enable us to find the velocity and acceleration of simple harmonic motion.

Eric S Calculus Lecture Proof Of The Derivative Of Sinx Youtube We’ll first use the definition of the derivative on the product. (fg)′ = lim h → 0f(x h)g(x h) − f(x)g(x) h. on the surface this appears to do nothing for us. we’ll first need to manipulate things a little to get the proof going. what we’ll do is subtract out and add in f(x h)g(x) to the numerator. We begin with the derivatives of the sine and cosine functions and then use them to obtain formulas for the derivatives of the remaining four trigonometric functions. calculating the derivatives of the sine and cosine functions will enable us to find the velocity and acceleration of simple harmonic motion.

How To Find The Derivative Of Xsinx From First Principles Youtube