Derivative Of Sin X Using First Principle Of Derivatives Epsilonify

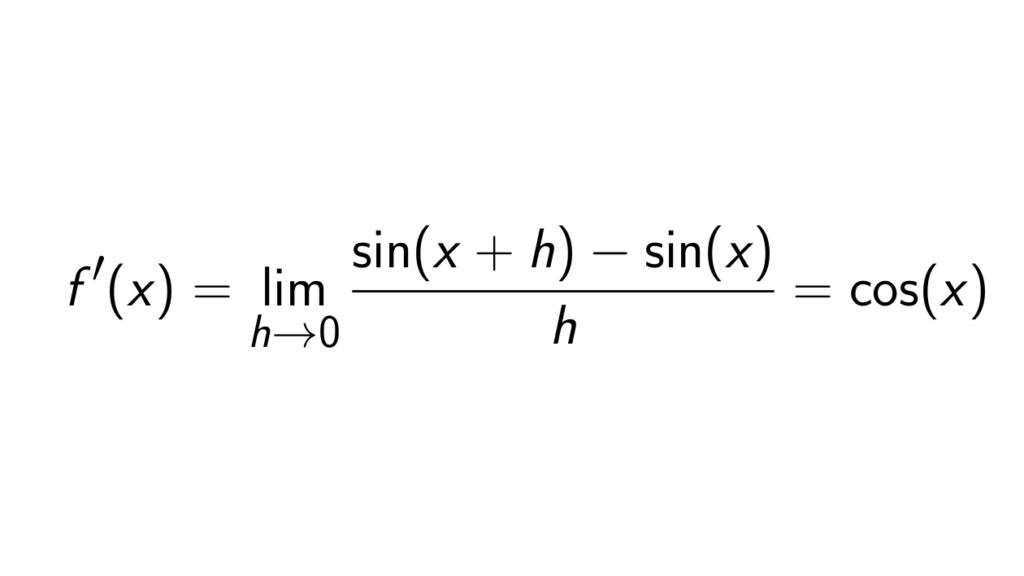
Derivative Of Sin X Using First Principle Of Derivatives Epsilonify In this article, we will prove the derivative of sinus, or in other words, the derivative of \sin (x) sin(x), using first principle of derivatives. we know that the derivative of \sin (x) sin(x) is \cos (x) cos(x), but we would also like to see how to prove that by the definition of the derivative. proof. let f (x) = \sin (x) f (x) = sin(x). then. Derivative of hyperbolic sine using first principle of derivatives. we will be proving that the derivative of \sinh (x) is equal to \cosh (x) by using the first principle of derivatives. proof. let f (x) = \sinh (x) = \frac {e^x e^ { x}} {2}. then by the first order principle, we have.

Calculus Differentiation Derivative Of Sin X From First Principle The derivative of \\sin(x) can be found from first principles. doing this requires using the angle sum formula for sin, as well as trigonometric limits. By definition, sin°(x) = sin(2π 360x) sin ° (x) = sin (2 π 360 x). if we agree that the symbol ° ° means 2π 360 2 π 360, then sin°(x) = sin(x°) sin ° (x) = sin (x °). it is easy to compute (sin°)′ (sin °) ′ using the chain rule, but it is also instructive to use differentiation from first principles:. To prove derivative of sin x using first principle of derivative, we will use basic limits and trigonometric formulas which are listed below: sin (x y) = sin x cos y sin y cos x. lim x→0 [sin x x] = 1. lim x→0 [ (cos x – 1) x] = 0. let’s start the proof for the derivative of sin x. by the first principle of derivative. 1. now apply limh → 0 to both sides, remembering that limh → 0sinh h = 1, and you should get your answer. if you want to calculate limh → 0cosh − 1 h just multiply the numerator and denominator by the conjugate, and remember the previous identity. spoiler alert: the answer is 0. share.

Derivative Of Sin X From First Principles Youtube To prove derivative of sin x using first principle of derivative, we will use basic limits and trigonometric formulas which are listed below: sin (x y) = sin x cos y sin y cos x. lim x→0 [sin x x] = 1. lim x→0 [ (cos x – 1) x] = 0. let’s start the proof for the derivative of sin x. by the first principle of derivative. 1. now apply limh → 0 to both sides, remembering that limh → 0sinh h = 1, and you should get your answer. if you want to calculate limh → 0cosh − 1 h just multiply the numerator and denominator by the conjugate, and remember the previous identity. spoiler alert: the answer is 0. share. Now, let us discuss the first principle method to find the derivative of sin x. derivative of sin x using the first principle method. the derivative of any function can be found using the limit definition of the derivative. (i.e) first principle. so, now we are going to apply the first principle method to find the derivative of sin x as well. The derivative of sin x can be determined using various methods, including the first principle method, chain rule, and quotient rule. each of these methods provides a different approach to finding the derivative, but they all yield the same result: cos x. derivative of sin x using the first principle method.

10 Find The Derivative Of The Following Function Using First Principle Now, let us discuss the first principle method to find the derivative of sin x. derivative of sin x using the first principle method. the derivative of any function can be found using the limit definition of the derivative. (i.e) first principle. so, now we are going to apply the first principle method to find the derivative of sin x as well. The derivative of sin x can be determined using various methods, including the first principle method, chain rule, and quotient rule. each of these methods provides a different approach to finding the derivative, but they all yield the same result: cos x. derivative of sin x using the first principle method.

Derivative Of Xsinx By First Principle Imath