Derivative Of Composite Function 2 Chain Rules Trig Function And

Derivative Of Composite Function 2 Chain Rules Trig Function And State the chain rule for the composition of two functions. apply the chain rule together with the power rule. apply the chain rule and the product quotient rules correctly in combination when both are necessary. recognize the chain rule for a composition of three or more functions. describe the proof of the chain rule. The inner function is 2𝑥 and its derivative is 2. we multiply sin(2𝑥) by 2 to get f'(x) = 2sin(2𝑥). the chain rule can be applied to trigonometric functions raised to a power. write the trigonometric function as the inner function in brackets and the power as the outer function.

Question Video Finding The Derivative Of A Composite Trigonometric Recall that the chain rule for the derivative of a composite of two functions can be written in the form \[\dfrac{d}{dx}\big(f(g(x))\big)=f′\big(g(x)\big)g′(x). \nonumber \] in this equation, both \(f(x)\) and \(g(x)\) are functions of one variable. now suppose that \(f\) is a function of two variables and \(g\) is a function of one variable. Activity 6.4.1: inner vs. outer functions. for each function given below, identify an inner function g and outer function f to write the function in the form f(g(x)). then, determine f ′ (x), g ′ (x), and f ′ (g(x)), and finally apply the chain rule (equation 6.4.18) to determine the derivative of the given function. All derivative rules apply when we differentiate trig functions. let’s look at how chain rule works in combination with trigonometric functions. keep in mind that everything we’ve learned about power rule, product rule, and quotient rule still applies. i create online courses to help you rock your math class. read more. This rule says that if we can identify the function as a composition of functions, then identify the inner function and the outer function. we ge t the derivative by doing the following, take the derivative of the outer function, copy the inner function, and multiply by the derivative of the inner function. first we’ll practice identifying.

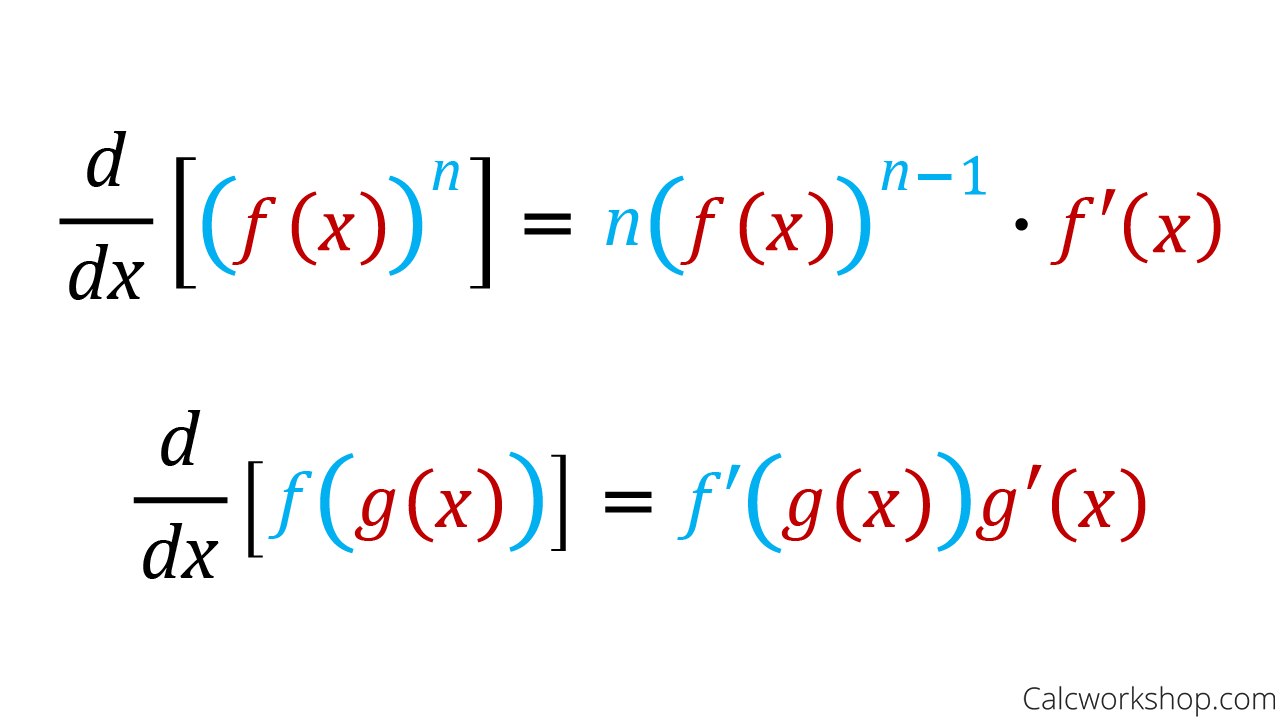
Chain Rule Explained W 7 Step By Step Examples All derivative rules apply when we differentiate trig functions. let’s look at how chain rule works in combination with trigonometric functions. keep in mind that everything we’ve learned about power rule, product rule, and quotient rule still applies. i create online courses to help you rock your math class. read more. This rule says that if we can identify the function as a composition of functions, then identify the inner function and the outer function. we ge t the derivative by doing the following, take the derivative of the outer function, copy the inner function, and multiply by the derivative of the inner function. first we’ll practice identifying. 3.6.1 state the chain rule for the composition of two functions. 3.6.2 apply the chain rule together with the power rule. 3.6.3 apply the chain rule and the product quotient rules correctly in combination when both are necessary. 3.6.4 recognize the chain rule for a composition of three or more functions. 3.6.5 describe the proof of the chain rule. 1f g 21x 2 f1g 1x 22. 1f g 2 the chain rule if f and g are functions that have derivatives, then the composite function h 1x 2 f1g 1x 22has a derivative given by h ¿1x 2 f¿1g 1x 22g ¿1x 2. chapter 2 99 in words, the chain rule says, the derivative of a composite function is the product of the derivative of the outer function evaluated at the.

The Chain Rule Derivatives Of Composite Trigonometric Functions Youtube 3.6.1 state the chain rule for the composition of two functions. 3.6.2 apply the chain rule together with the power rule. 3.6.3 apply the chain rule and the product quotient rules correctly in combination when both are necessary. 3.6.4 recognize the chain rule for a composition of three or more functions. 3.6.5 describe the proof of the chain rule. 1f g 21x 2 f1g 1x 22. 1f g 2 the chain rule if f and g are functions that have derivatives, then the composite function h 1x 2 f1g 1x 22has a derivative given by h ¿1x 2 f¿1g 1x 22g ¿1x 2. chapter 2 99 in words, the chain rule says, the derivative of a composite function is the product of the derivative of the outer function evaluated at the.

Derivatives Trig Functions Chain Rule Double Chain Rule Youtube