Demostracion De La Suma De Los Angulos Interiores De Un Triangulo
Demostración Suma De ángulos Interiores De Triangulo Geogebra Teorema de suma de triángulo. el teorema de la suma del triángulo dice que los tres ángulos interiores de cualquier triángulo suman 180∘ 180 ∘. figura 4.17.1 4.17. 1. m∠1 m∠2 m∠3 = 180∘ m ∠ 1 m ∠ 2 m ∠ 3 = 180 ∘. aquí hay una prueba del teorema de la suma del triángulo. 👇👇 información importante en la descripciÓn 👇👇😎 este video lo hice para que te vaya mejor en tus estudios de matemáticas 👍 se parte de la comunidad mat.

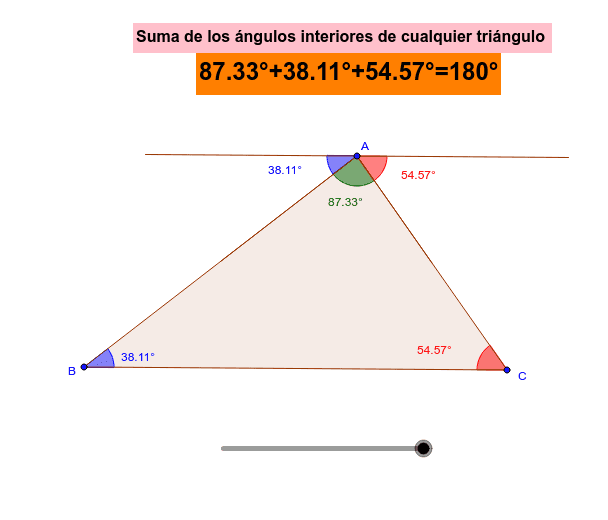
Suma De Los ángulos Interiores De Un Triángulo Teorema Para La demostración de que la suma de los ángulos interiores de un triángulo es 180° es un ejercicio básico en geometría. se puede llevar a cabo utilizando el concepto de líneas paralelas y transversales: dibuja un triángulo cualquiera, denotémoslo como abc. extiende la base del triángulo, por ejemplo, la línea que va de a a b. Esta es una de las formas de demostrar que la suma de los ángulos interiores de un polígono simple de lados siempre es igual a (). en particular, esta propiedad asegura que la suma de los ángulos de un cuadrilátero simple es siempre igual a 360°. si un cuadrilátero simple tiene tres ángulos rectos, entonces su cuarto ángulo también es. Calcular el tercer ángulo de un triángulo es sencillo si conocemos la medida de los otros dos ángulos. para ello, simplemente restamos la suma de los dos ángulos internos conocidos de 180°. la fórmula es la siguiente: c = 180° – (a b) por ejemplo, si tenemos un triángulo donde a = 50° y b = 60°, podemos calcular c: c = 180. Teorema de la suma de los ángulos internos de un triángulo. el teorema fundamental que gobierna la relación entre los ángulos internos de un triángulo es una pieza central en la geometría euclidiana. a través de este teorema, se revela una verdad universal que se aplica a todos los triángulos, independientemente de su forma, tamaño o tipo.

Demostración De Que La Suma De Los ángulos Internos En Un Triángulo Da Calcular el tercer ángulo de un triángulo es sencillo si conocemos la medida de los otros dos ángulos. para ello, simplemente restamos la suma de los dos ángulos internos conocidos de 180°. la fórmula es la siguiente: c = 180° – (a b) por ejemplo, si tenemos un triángulo donde a = 50° y b = 60°, podemos calcular c: c = 180. Teorema de la suma de los ángulos internos de un triángulo. el teorema fundamental que gobierna la relación entre los ángulos internos de un triángulo es una pieza central en la geometría euclidiana. a través de este teorema, se revela una verdad universal que se aplica a todos los triángulos, independientemente de su forma, tamaño o tipo. 1. define la propiedad de la suma de los ángulos. la propiedad de la suma de los ángulos de un triángulo establece que los ángulos de cualquier triángulo siempre suman 180º. [6] todos los triángulos tienen 3 ángulos y, ya sean agudos, obtusos o rectángulos, estos suman siempre 180º. por ejemplo, en el triángulo abc, el ángulo a el. La suma total de los tres ángulos interiores de cualquier triángulo siempre es igual a 180°. podemos verificar esto usando el siguiente diagrama: la línea x es paralela a la base del triángulo, es decir, a la línea bc. sabemos que cuando dos líneas paralelas son intersecadas por una transversal, formamos ángulos correspondientes y.

Suma De ángulos Internos De Un Triángulo Youtube 1. define la propiedad de la suma de los ángulos. la propiedad de la suma de los ángulos de un triángulo establece que los ángulos de cualquier triángulo siempre suman 180º. [6] todos los triángulos tienen 3 ángulos y, ya sean agudos, obtusos o rectángulos, estos suman siempre 180º. por ejemplo, en el triángulo abc, el ángulo a el. La suma total de los tres ángulos interiores de cualquier triángulo siempre es igual a 180°. podemos verificar esto usando el siguiente diagrama: la línea x es paralela a la base del triángulo, es decir, a la línea bc. sabemos que cuando dos líneas paralelas son intersecadas por una transversal, formamos ángulos correspondientes y.

Comments are closed.