Degree Of Polynomial Definition How To Find Degree Of Polynomial

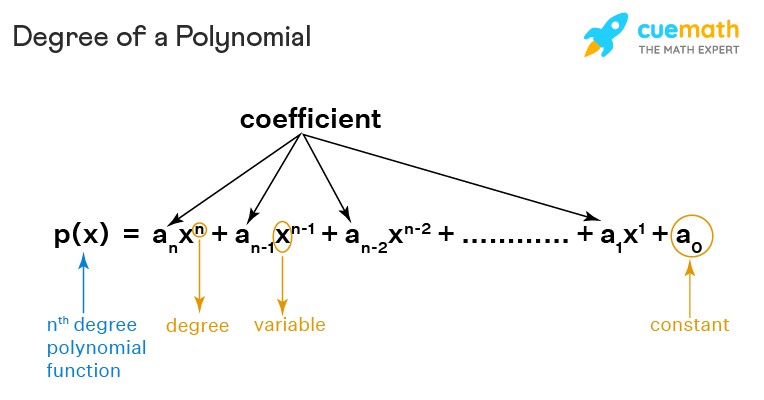
Degree Of Polynomial Definition How To Find Degree Of Polynomial The degree of a polynomial with more than one variable can be calculated by adding the exponents of each variable in it. for example: 5x 3 6x 2 y 2 2xy. 5x 3 has a degree of 3 (x has an exponent of 3). 6x 2 y 2 has a degree of 4 (x has an exponent of 2, y has 2, so 2 2=4). 2xy has a degree of 2 (x has an exponent of 1, y has 1, so 1 1=2). A polynomial is merging of variables assigned with exponential powers and coefficients. the steps to find the degree of a polynomial are as follows: for example if the expression is : 5x 5 7x 3 2x 5 3x 2 5 8x 4. step 1: combine all the like terms that are the terms with the variable terms. (5x 5 2x 5) 7x 3 3x 2 8x (5 4.

Degree Of Polynomial Polynomials Basic Math Degree Of A Polynomial Step 2: find the degree of each term. to find the degree of a term, add the exponents of variables present. step 3: compare the degrees of individual terms. the highest degree among them is the degree of the polynomial. example: a b 6 − a 4 b 8 a b. degree of a b 6 = 1 6 = 7. degree of a 4 b 8 = 4 8 = 12. To find the degree of a polynomial with one variable, combine the like terms in the expression so you can simplify it. next, drop all of the constants and coefficients from the expression. then, put the terms in decreasing order of their exponents and find the power of the largest term. In mathematics, the degree of a polynomial is the highest of the degrees of the polynomial's monomials (individual terms) with non zero coefficients. the degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non negative integer. for a univariate polynomial, the degree of the polynomial is simply the. The degree is the value of the greatest exponent of any expression (except the constant) in the polynomial. to find the degree all that you have to do is find the largest exponent in the polynomial. note: ignore coefficients coefficients have nothing to do with the degree of a polynomial.

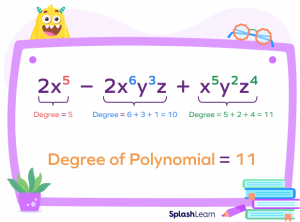
Degree Of A Polynomial Definition Types Examples Facts In mathematics, the degree of a polynomial is the highest of the degrees of the polynomial's monomials (individual terms) with non zero coefficients. the degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non negative integer. for a univariate polynomial, the degree of the polynomial is simply the. The degree is the value of the greatest exponent of any expression (except the constant) in the polynomial. to find the degree all that you have to do is find the largest exponent in the polynomial. note: ignore coefficients coefficients have nothing to do with the degree of a polynomial. How to find the degree of a polynomial function. the mathematical definition of a polynomial is as follows: p (x) = a n x n a 2 x 2 a 1 ″ x ″ a 0. in this definition, the a 's. With more than one variable. for each term: find the degree by adding the exponents of each variable in it, the largest such degree is the degree of the polynomial. example: what is the degree of this polynomial: checking each term: 5xy2 has a degree of 3 (x has an exponent of 1, y has 2, and 1 2=3) 3x has a degree of 1 (x has an exponent of 1).

Learn How To Find The Degree Of A Polynomial Youtube How to find the degree of a polynomial function. the mathematical definition of a polynomial is as follows: p (x) = a n x n a 2 x 2 a 1 ″ x ″ a 0. in this definition, the a 's. With more than one variable. for each term: find the degree by adding the exponents of each variable in it, the largest such degree is the degree of the polynomial. example: what is the degree of this polynomial: checking each term: 5xy2 has a degree of 3 (x has an exponent of 1, y has 2, and 1 2=3) 3x has a degree of 1 (x has an exponent of 1).