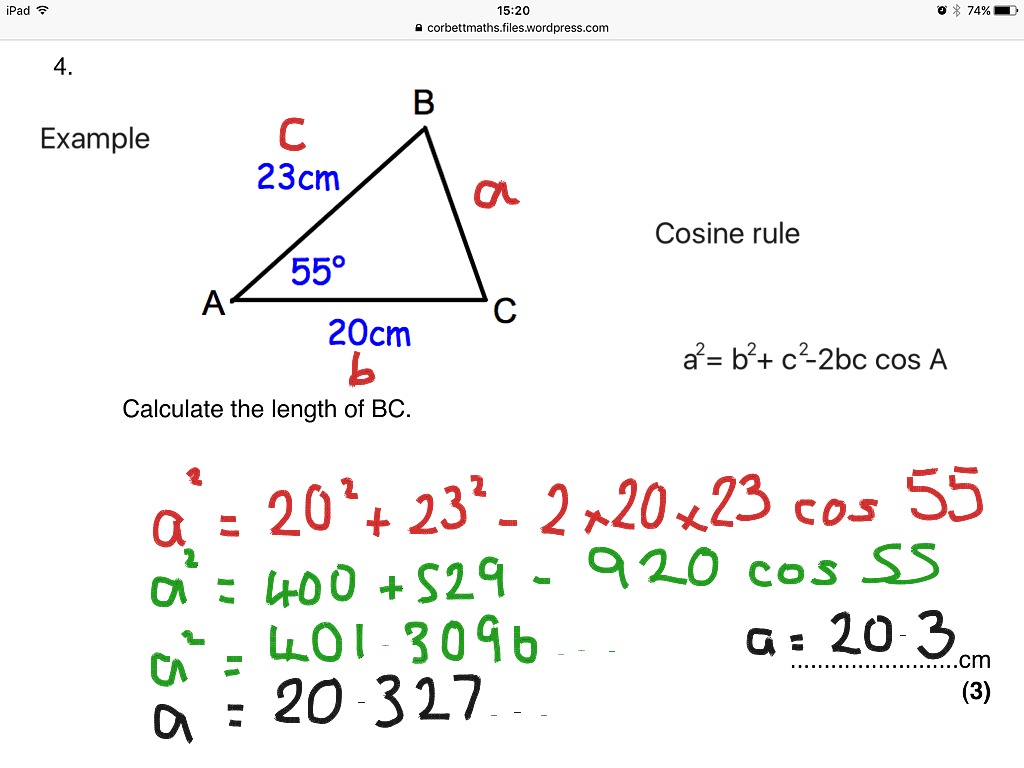
Cosine Rule Finding A Missing Side

Using The Cosine Rule To Find Sides Advanced Trigonometry Tutorial We just saw how to find an angle when we know three sides. it took quite a few steps, so it is easier to use the "direct" formula (which is just a rearrangement of the c 2 = a 2 b 2 − 2ab cos(c) formula). it can be in either of these forms: cos(c) = a 2 b 2 − c 2 2ab. cos(a) = b 2 c 2 − a 2 2bc. cos(b) = c 2 a 2 − b 2 2ca. Example 3: find the missing side using the cosine rule. find the length of z for triangle xyz. write your answer to a suitable degree of accuracy. label each angle (a, b, c) and each side (a, b, c) of the triangle. show step. in order to find the length of z, we need to know the opposite angle at z.

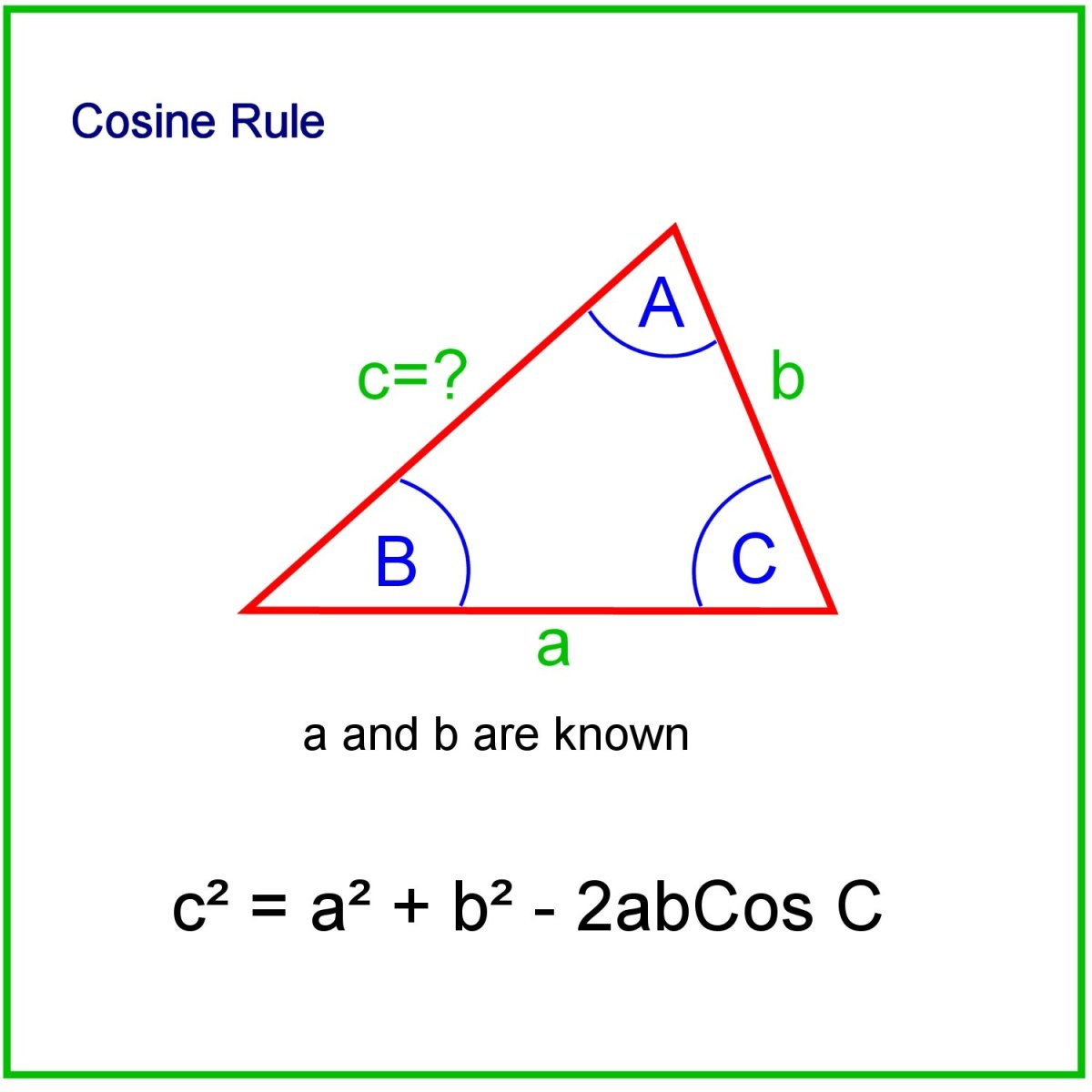
Cosine Rule Find A Side Youtube The cosine rule, also known as the law of cosines, relates all 3 sides of a triangle with an angle of a triangle. it is most useful for solving for missing information in a triangle. for example, if all three sides of the triangle are known, the cosine rule allows one to find any of the angle measures. similarly, if two sides and the angle between them is known, the cosine rule allows …. Example 1: find a missing side using the cosine rule. find the value of x x for triangle abc, abc, correct to 2 2 decimal places. \textbf { (a, \, b, \, c)} (a, b, c) of the triangle. 2 state the law of cosines, then substitute the given values into the formula. Cosine rule is also called law of cosines or cosine formula. suppose, a, b and c are lengths of the side of a triangle abc, then; a2 = b2 c2 – 2bc cos ∠x. b2 = a2 c2 – 2ac cos ∠y. c2 = a2 b2 – 2ab cos ∠z. where ∠x, ∠y and ∠z are the angles between the sides of the triangle. the cosine rule relates to the lengths of the. The sine rule can be used to find an angle from 3 sides and an angle, or a side from 3 angles and a side. the cosine rule can find a side from 2 sides and the included angle, or an angle from 3 sides.
Cosine Rule To Find A Missing Side Math Trigonometry Showme Cosine rule is also called law of cosines or cosine formula. suppose, a, b and c are lengths of the side of a triangle abc, then; a2 = b2 c2 – 2bc cos ∠x. b2 = a2 c2 – 2ac cos ∠y. c2 = a2 b2 – 2ab cos ∠z. where ∠x, ∠y and ∠z are the angles between the sides of the triangle. the cosine rule relates to the lengths of the. The sine rule can be used to find an angle from 3 sides and an angle, or a side from 3 angles and a side. the cosine rule can find a side from 2 sides and the included angle, or an angle from 3 sides. Now, let us use the law of the cosine equation to find the missing side. example: two sides of a triangle measure 72 in and 50 in with the angle between them measuring 49º let us find the missing side. solution: substitute 72 for b, 50 for c and 49º for a. using the law of cosines formula, a 2 = b 2 c 2 2bc·cosa. a 2 = (72) 2 (50) 2. The cosine rule is a commonly used rule in trigonometry. it can be used to investigate the properties of non right triangles and thus allows you to find missing information, such as side lengths and angle measurements. the formula is similar to the pythagorean theorem and relatively easy to memorize.
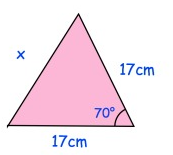
Find The Missing Side And Angle Of A Triangle Using Cosine Rule Now, let us use the law of the cosine equation to find the missing side. example: two sides of a triangle measure 72 in and 50 in with the angle between them measuring 49º let us find the missing side. solution: substitute 72 for b, 50 for c and 49º for a. using the law of cosines formula, a 2 = b 2 c 2 2bc·cosa. a 2 = (72) 2 (50) 2. The cosine rule is a commonly used rule in trigonometry. it can be used to investigate the properties of non right triangles and thus allows you to find missing information, such as side lengths and angle measurements. the formula is similar to the pythagorean theorem and relatively easy to memorize.

The Cosine Rule Missing Sides Youtube
How To Calculate The Sides And Angles Of Triangles Using Pythagoras

Comments are closed.