Corresponding Angles Definition Types And Example Cuemath

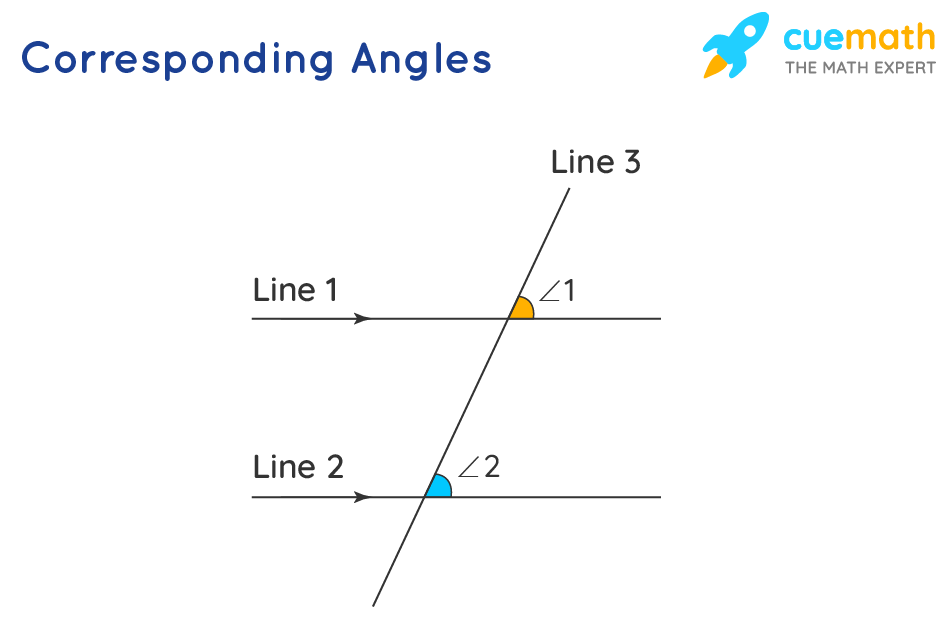
Corresponding Angles Definition Types And Example Cuemath Corresponding angles. corresponding angles are one of the types of angles that are formed when two parallel lines are intersected by the transversal. these are formed in the matching corners or corresponding corners with the transversal. corresponding angles have important applications in the areas of mathematics and physics. Example 3: the values of two corresponding angles ∠1 = 3x 1 and ∠5 = 4x – 3. solve for the value of x. answer: as they are corresponding angles and the lines are said to be parallel in nature, then they should be congruent. equate the given expressions ∠1 = 3x 1 and ∠5 = 4x – 3 and find the value of x.

Corresponding Angles Definition Theorem Examples We will now go on to the specific case of two parallel lines being cut by a transversal. the following are the properties of the 8 angles so formed. all the corresponding angles are equal. ∠1 = ∠5. ∠2 = ∠6. ∠4 = ∠8. ∠3 = ∠7. all the alternate interior angles are equal. ∠3 = ∠5. Those are called transversal angles. those types of angles on a transversal are given below: corresponding angles; alternate interior angles; alternate exterior angles; co interior angles; from the given diagram, if we try to organize the angles based on the relative positions they occupy, we get the following categories of angles. 2x = 11. x = 112. x = 5.5. 2. if eg and bd are two parallel lines, find the measure of the angle x. solution: the angles ∠gfh and ∠efc are vertically opposite angles. vertical angles are always congruent. thus, m∠cfe = m∠gfh = 48°. now, the angles ∠efc and ∠bca are corresponding angles formed by parallel lines. Corresponding angles are pairs of angles that occupy the same relative position at each intersection when a transversal intersects two parallel straight lines. corresponding angles. the above figure shows two parallel lines ab and cd intersected by the transversal gh. the pairs of corresponding angles in the given figure are: ∠1 and ∠5.

Corresponding Angles Definition Theorem Examples 2x = 11. x = 112. x = 5.5. 2. if eg and bd are two parallel lines, find the measure of the angle x. solution: the angles ∠gfh and ∠efc are vertically opposite angles. vertical angles are always congruent. thus, m∠cfe = m∠gfh = 48°. now, the angles ∠efc and ∠bca are corresponding angles formed by parallel lines. Corresponding angles are pairs of angles that occupy the same relative position at each intersection when a transversal intersects two parallel straight lines. corresponding angles. the above figure shows two parallel lines ab and cd intersected by the transversal gh. the pairs of corresponding angles in the given figure are: ∠1 and ∠5. Types of angles. in geometry, there are many types of angles such as congruent, adjacent, vertical, corresponding, alternating, exterior, and interior angles. all angles have relationships to other angles and those angle relationships are what we will cover here. get free estimates from geometry tutors near you. Two angles correspond or relate to each other by being on the same side of the transversal. one is an exterior angle (outside the parallel lines), and one is an interior angle (inside the parallel lines). corresponding angles are just one type of angle pair. angles that are on the opposite side of the transversal are called alternate angles.