Corresponding Angles Definition Theorem With Examples

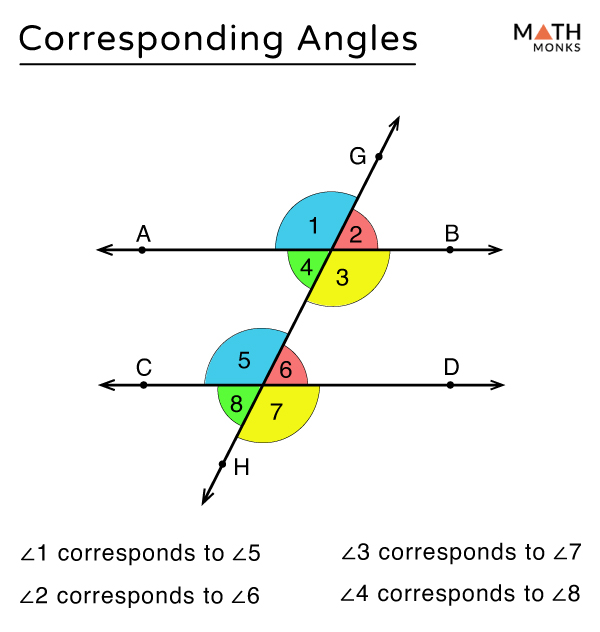
Corresponding Angles Definition Theorem With Examples Corresponding angles in geometry are defined as the angles which are formed at corresponding corners when two parallel lines are intersected by a transversal. i.e., two angles are said to be corresponding angles if: the angles lie at different corners. they lie on the same (corresponding) side of the transversal. Corresponding angles are pairs of angles that occupy the same relative position at each intersection when a transversal intersects two parallel straight lines. corresponding angles. the above figure shows two parallel lines ab and cd intersected by the transversal gh. the pairs of corresponding angles in the given figure are: ∠1 and ∠5.

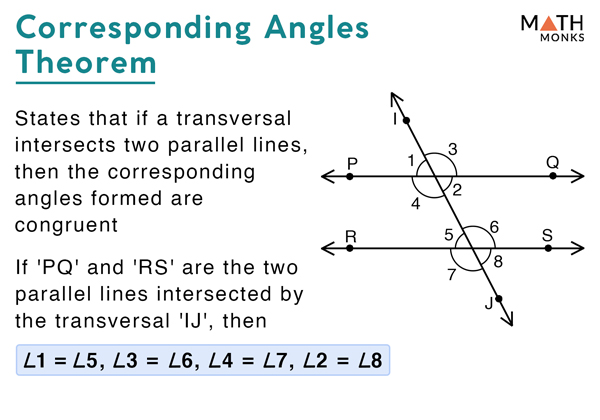
Corresponding Angles Definition Theorem With Examples A corresponding angle is one that holds the same relative position as another angle somewhere else in the figure. corresponding angles in plane geometry are created when transversals cross two lines. two angles correspond or relate to each other by being on the same side of the transversal. one is an exterior angle (outside the parallel lines. 2x = 11. x = 112. x = 5.5. 2. if eg and bd are two parallel lines, find the measure of the angle x. solution: the angles ∠gfh and ∠efc are vertically opposite angles. vertical angles are always congruent. thus, m∠cfe = m∠gfh = 48°. now, the angles ∠efc and ∠bca are corresponding angles formed by parallel lines. When two lines are crossed by another line (called the transversal): the angles in matching corners are called corresponding angles. in this example a and e are corresponding angles. also: • b and f are corresponding angles. • c and g are corresponding angles. • d and h are corresponding angles. Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. they are usually formed when two parallel or non parallel lines are cut by a transversal. in our illustration above, parallel lines are cut by a transversal which as a result, formed 4 corresponding angles.

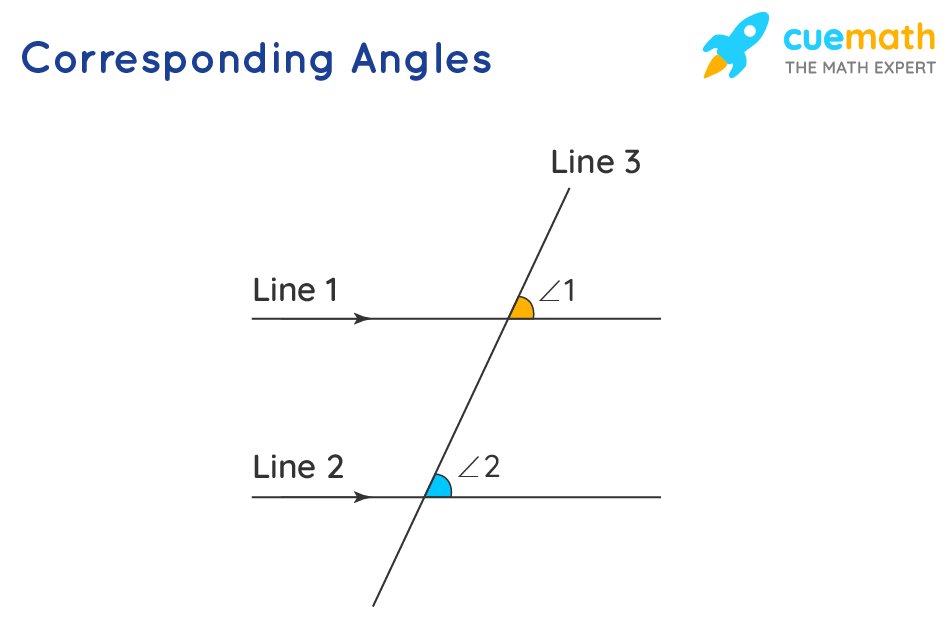
Corresponding Angles Definition Theorem Examples When two lines are crossed by another line (called the transversal): the angles in matching corners are called corresponding angles. in this example a and e are corresponding angles. also: • b and f are corresponding angles. • c and g are corresponding angles. • d and h are corresponding angles. Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. they are usually formed when two parallel or non parallel lines are cut by a transversal. in our illustration above, parallel lines are cut by a transversal which as a result, formed 4 corresponding angles. Corresponding angles. definition: corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line (i.e. the transversal). for example, in the below given figure, angle p and angle w are the corresponding angles. The corresponding angle theorem states that, if a line intersects two parallel lines, then the corresponding angles in the two intersections are congruent. say, for example, in the figure, since we know that line 1 ∥ line 2 and line 3 is the transversal line, then ∠1 is corresponding to ∠2. hence, we can say that the angle that exists.

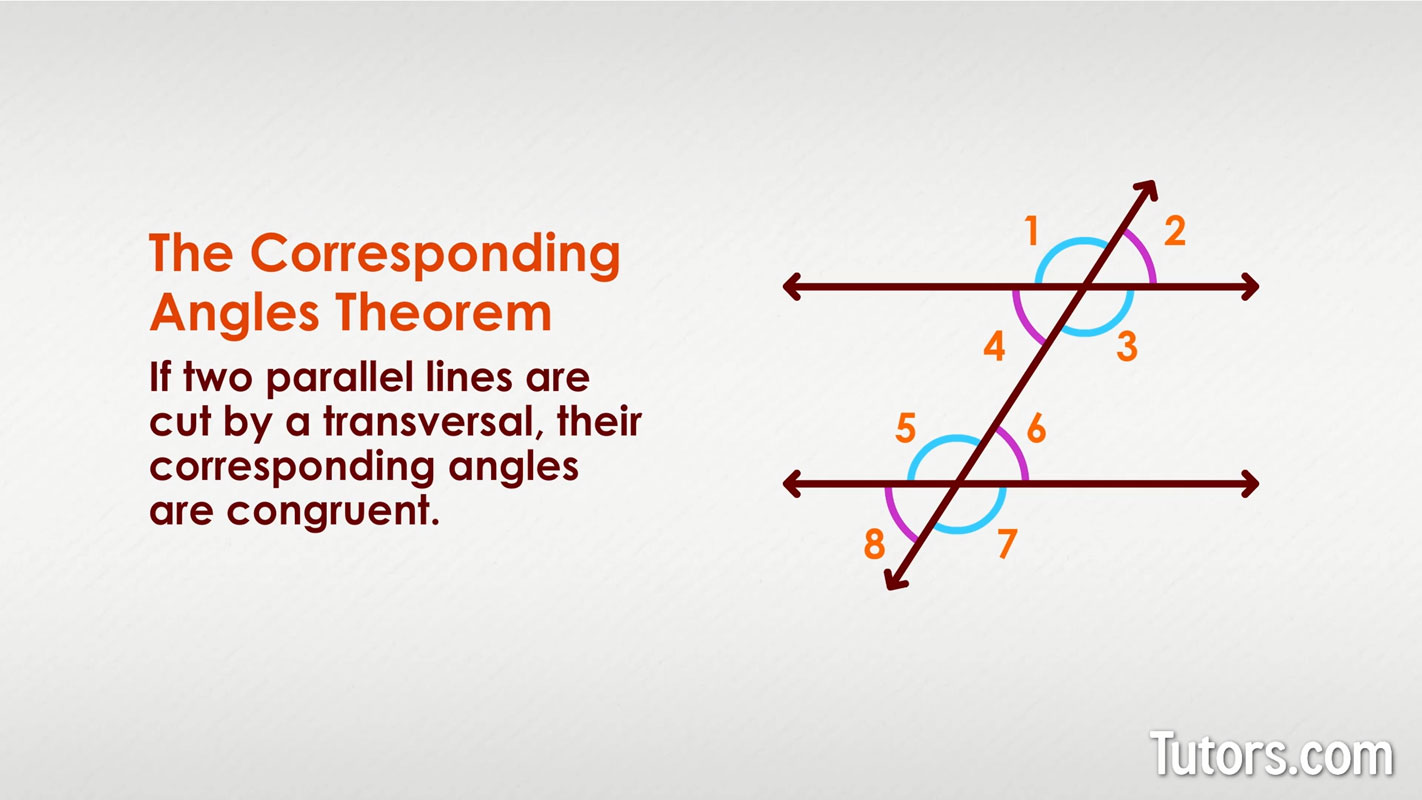
Corresponding Angles Definition Theorem Examples Corresponding angles. definition: corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line (i.e. the transversal). for example, in the below given figure, angle p and angle w are the corresponding angles. The corresponding angle theorem states that, if a line intersects two parallel lines, then the corresponding angles in the two intersections are congruent. say, for example, in the figure, since we know that line 1 ∥ line 2 and line 3 is the transversal line, then ∠1 is corresponding to ∠2. hence, we can say that the angle that exists.

Corresponding Angles Definition Types And Example Cuemath

Corresponding Angles Definition Theorem Examples