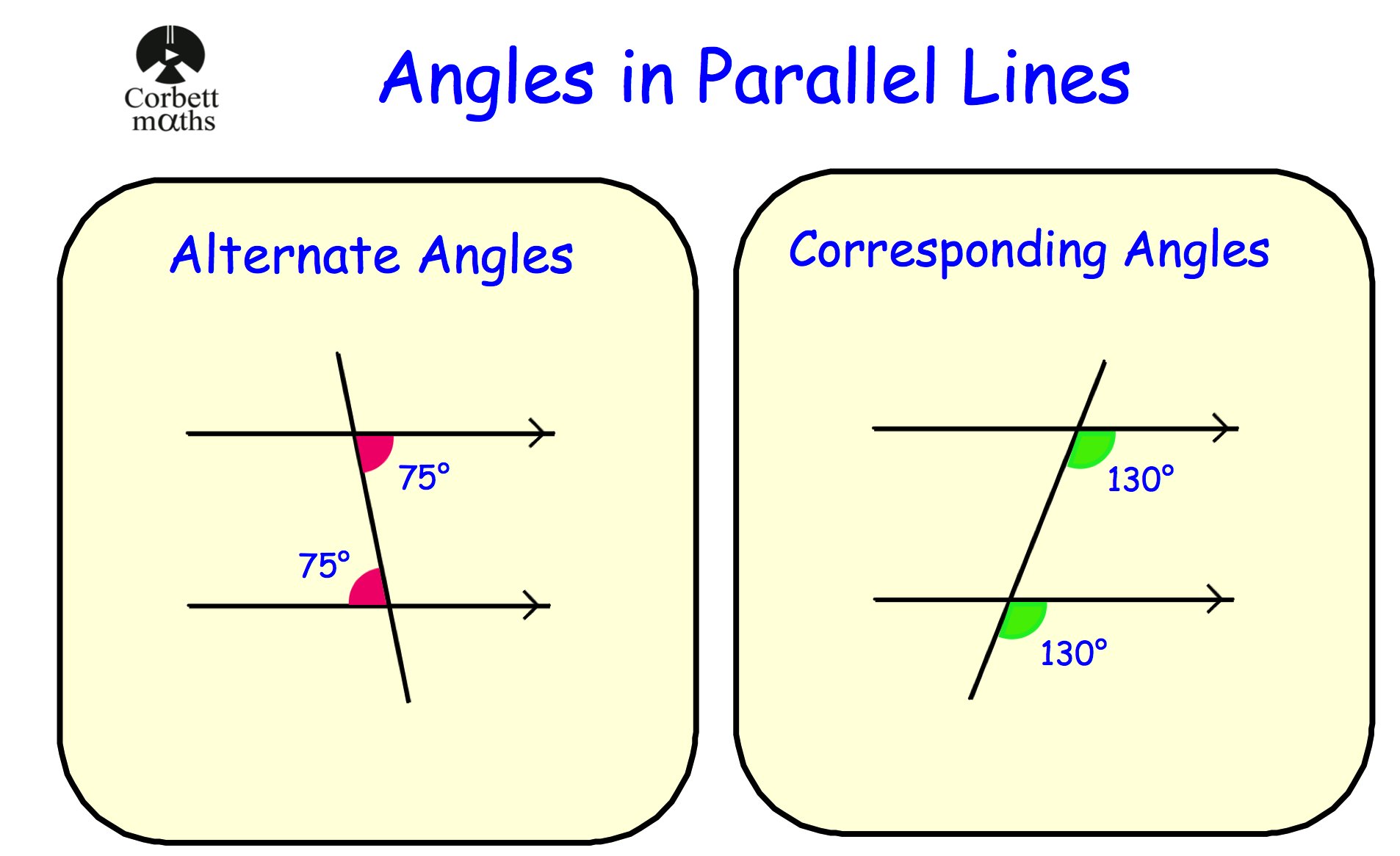
Properties Of Corresponding Angles Corresponding angles appears when a parallel line is intersected by a transversal. those angles are said to the congruent.#shorts #parallellines #geometry #c. Example 2: find pairs of corresponding angles. ← s→ y s y and ← t → z t z are parallel lines. name all pairs of corresponding angles. identify two parallel lines that are intersected by a transversal. show step. the two parallel lines are sy s y and t z. tz. line u x u x is the transversal.
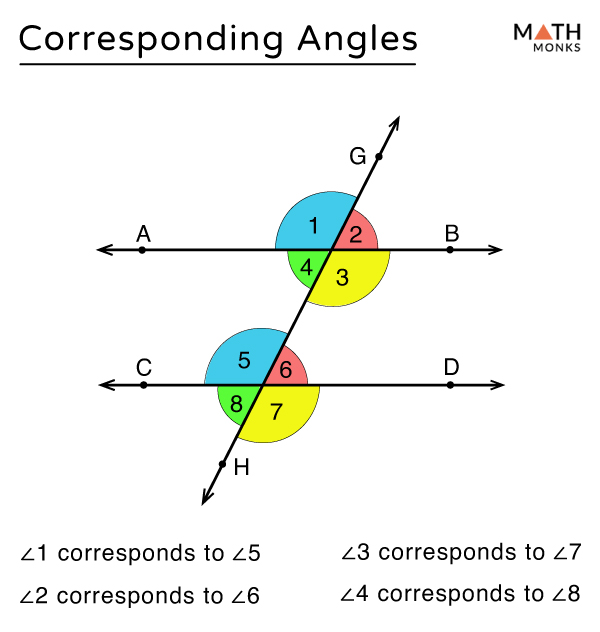
Corresponding Angles Definition Theorem With Examples When two lines are crossed by another line (called the transversal): the angles in matching corners are called corresponding angles. in this example a and e are corresponding angles. also: • b and f are corresponding angles. • c and g are corresponding angles. • d and h are corresponding angles. Angle relationships corresponding angles. we can adroitly pull from this figure angles that look like each other. angles that have the same position relative to one another in the two sets of four angles (four at the top, line ar; four at the bottom, line to) are corresponding angles. when the corresponding angles are on parallel lines, they. The angles lie on the same side of the transversal in "corresponding" positions. when the lines are parallel, the measures are equal. ∠1 and ∠2 are corresponding angles. ∠3 and ∠4 are corresponding angles. ∠5 and ∠6 are corresponding angles. ∠7 and ∠8 are corresponding angles. Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. they are usually formed when two parallel or non parallel lines are cut by a transversal. in our illustration above, parallel lines are cut by a transversal which as a result, formed 4 corresponding angles.
How To Find Corresponding Angles Of Parallel Lines Given One Angle The angles lie on the same side of the transversal in "corresponding" positions. when the lines are parallel, the measures are equal. ∠1 and ∠2 are corresponding angles. ∠3 and ∠4 are corresponding angles. ∠5 and ∠6 are corresponding angles. ∠7 and ∠8 are corresponding angles. Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. they are usually formed when two parallel or non parallel lines are cut by a transversal. in our illustration above, parallel lines are cut by a transversal which as a result, formed 4 corresponding angles. The other corresponding pairs of angles in the above diagram are: b and f; c and g; a and e. (corresponding angles found in a f shaped figure) example: in the following diagram, all the lines shown are straight lines. line m is parallel to line n. list a pair of corresponding angle. solution: d and h are corresponding angles. Example 1: line m is parallel to line n and l is the transversal forming angles a and b, where ∠ a and ∠ b are corresponding angles. ∠ a measures 43 °, what is the measure of ∠ b? solution: ∠ a and ∠ b are corresponding angles formed by parallel lines and a transversal. so, ∠ a = ∠ b. ∠ a = 43 °. so, m ∠ b = 43 ∘.
Comments are closed.