Corresponding Angle Relationships A
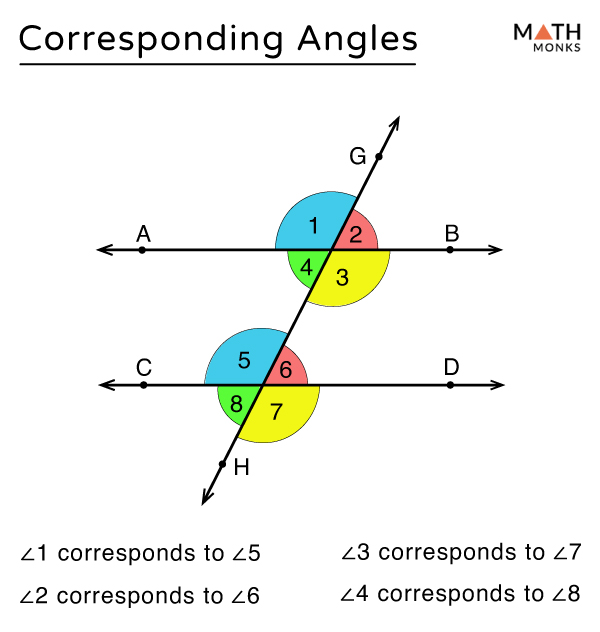
Corresponding Angles Definition Theorem With Examples Types of angles. in geometry, there are many types of angles such as congruent, adjacent, vertical, corresponding, alternating, exterior, and interior angles. all angles have relationships to other angles and those angle relationships are what we will cover here. get free estimates from geometry tutors near you. When two lines are crossed by another line (called the transversal): the angles in matching corners are called corresponding angles. in this example a and e are corresponding angles. also: • b and f are corresponding angles. • c and g are corresponding angles. • d and h are corresponding angles.

How Do You Construct Corresponding Angles Socratic Example 2: find pairs of corresponding angles. ← s→ y s y and ← t → z t z are parallel lines. name all pairs of corresponding angles. identify two parallel lines that are intersected by a transversal. show step. the two parallel lines are sy s y and t z. tz. line u x u x is the transversal. Refer to the figure below. the corresponding angles are the angles that lie on the same side of the transversal in matching corners. in other words, they occupy the same relative position in the figure. in a pair of corresponding angles, one is an exterior angle and one is an interior angle. in the figure, transversal l intersects lines m and n. Corresponding angles in geometry are defined as the angles which are formed at corresponding corners when two parallel lines are intersected by a transversal. i.e., two angles are said to be corresponding angles if: the angles lie at different corners. they lie on the same (corresponding) side of the transversal. Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. they are usually formed when two parallel or non parallel lines are cut by a transversal. in our illustration above, parallel lines are cut by a transversal which as a result, formed 4 corresponding angles.

Corresponding Angles Graph At Kathleen Swope Blog Corresponding angles in geometry are defined as the angles which are formed at corresponding corners when two parallel lines are intersected by a transversal. i.e., two angles are said to be corresponding angles if: the angles lie at different corners. they lie on the same (corresponding) side of the transversal. Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. they are usually formed when two parallel or non parallel lines are cut by a transversal. in our illustration above, parallel lines are cut by a transversal which as a result, formed 4 corresponding angles. 2x = 11. x = 112. x = 5.5. 2. if eg and bd are two parallel lines, find the measure of the angle x. solution: the angles ∠gfh and ∠efc are vertically opposite angles. vertical angles are always congruent. thus, m∠cfe = m∠gfh = 48°. now, the angles ∠efc and ∠bca are corresponding angles formed by parallel lines. Example 1: given the diagram below, determine the values of the angles x, y and z. solution: step 1: x is a supplement of 65°. therefore, x 65° = 180° ⇒ x = 180° – 65° = 115°. step 2: z and 115° are vertical angles. therefore, z = 115°. step 3: y and 65° are vertical angles. therefore, y = 65°.

8 G 5 Angle Relationships Mr Hill S Math 2x = 11. x = 112. x = 5.5. 2. if eg and bd are two parallel lines, find the measure of the angle x. solution: the angles ∠gfh and ∠efc are vertically opposite angles. vertical angles are always congruent. thus, m∠cfe = m∠gfh = 48°. now, the angles ∠efc and ∠bca are corresponding angles formed by parallel lines. Example 1: given the diagram below, determine the values of the angles x, y and z. solution: step 1: x is a supplement of 65°. therefore, x 65° = 180° ⇒ x = 180° – 65° = 115°. step 2: z and 115° are vertical angles. therefore, z = 115°. step 3: y and 65° are vertical angles. therefore, y = 65°.
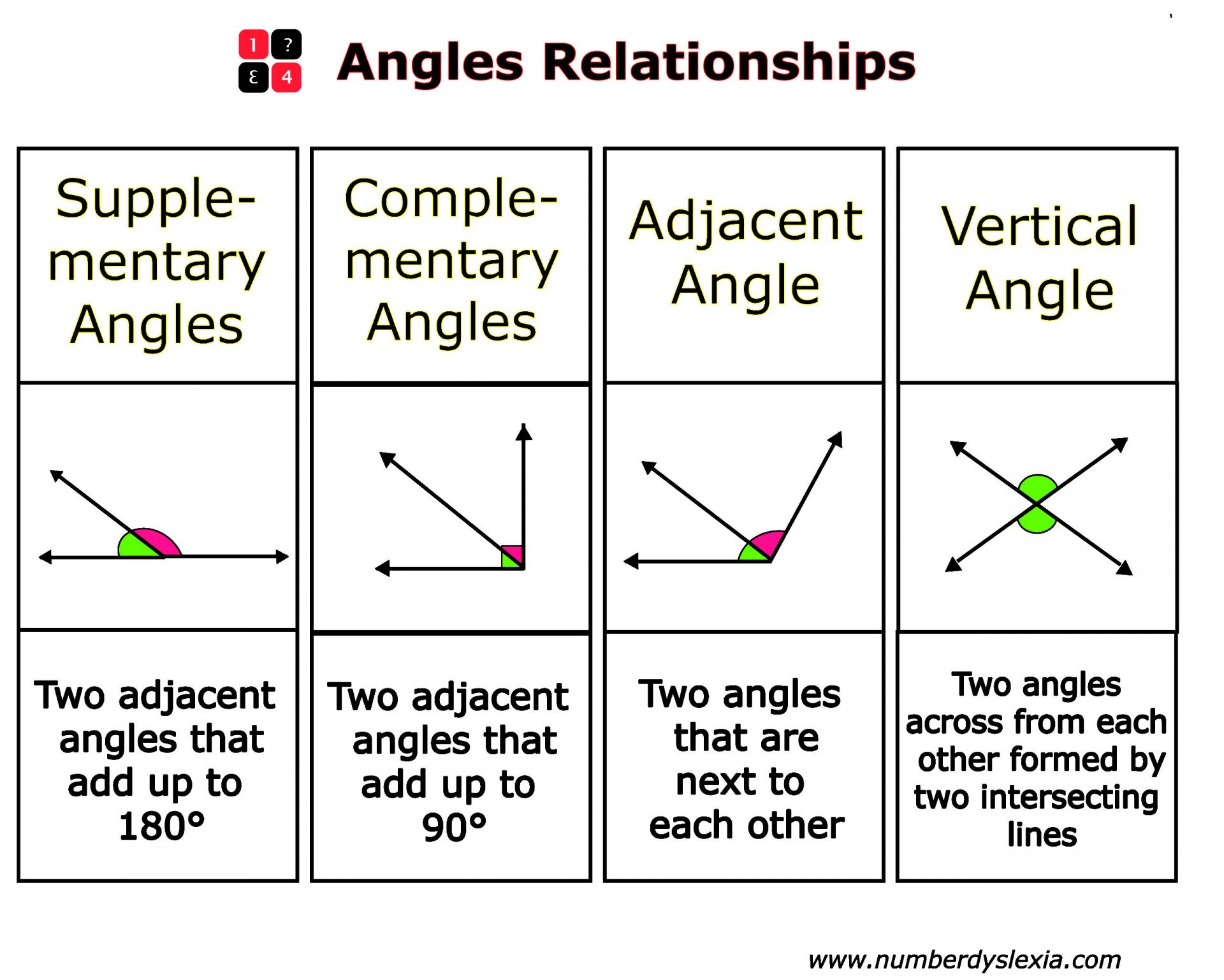
Free Printable Angles Anchor Chart For Classroom Pdf Number Dyslexia
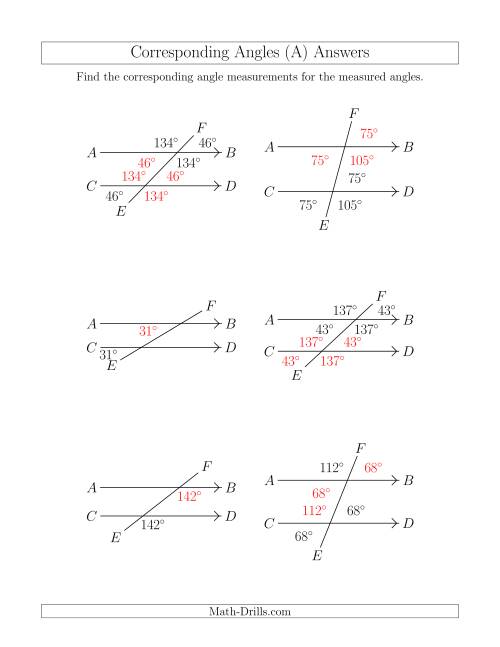
Corresponding Angle Relationships A

Comments are closed.