Construction Of Tangents To A Circle Geometry

Construction Of Tangents To A Circle From A Point Outside A Circle Step 1: draw a circle with the required radius with centre o. step 2: join centre of the circle o and any point p on the circle. op is the radius of the circle. step 3: draw a line perpendicular to radius op through point p. this line will be a tangent to the circle at p. two tangents can be drawn to a circle from a point outside of the circle. Steps: draw a line connecting the point to the center of the circle. construct the perpendicular bisector of that line. place the compass on the midpoint, adjust its length to reach the end point, and draw an arc across the circle. where the arc crosses the circle will be the tangent points. geometric constructions.
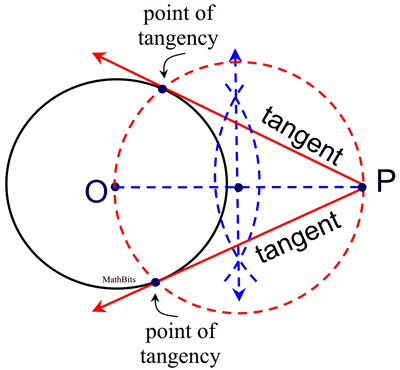
Construct Tangents To Circles Mathbitsnotebook Geo It is a line from the center to the given point p on the circle. 2: sp is perpendicular to or: by construction, sp is the perpendicular to or at p. see constructing a perpendicular to a line at a point for method and proof. 3: sp is the tangent to o at the point p: the tangent line is at right angles to the radius at the point of contact. A tangent to a circle is a line which intersects the circle in exactly one point. in figure 1 line ab←→ a b ↔ is a tangent, intersecting circle o o just at point p p. figure 1. ab←→ a b ↔ is tangent to circle o o at point p p. a tangent has the following important property: theorem 7.3.1 7.3. 1. a tangent is perpendicular to the. Remove parentheses and subtract 360 from both sides: –2∠mjp –2∠ojm = –180. divide through by –2:: ∠mjp ∠ojm = 90. 8. jp is a tangent to circle o and passes through p. jp is a tangent to o because it touches the circle at j and is at right angles to a radius at the contact point. (see tangent to a circle.). In euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. since the tangent line to a circle at a point p is.
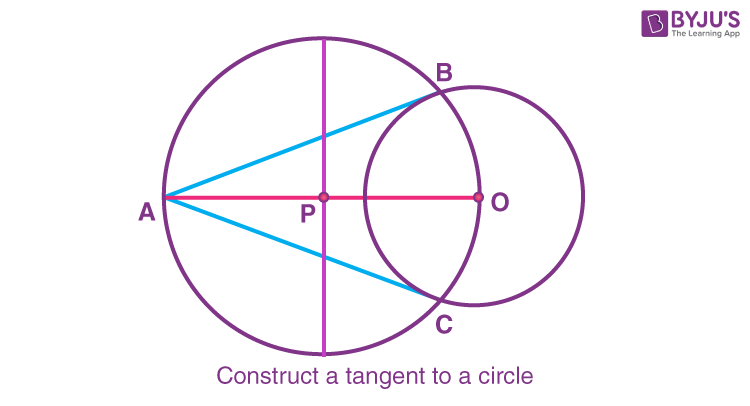
Construction Of Tangent To A Circle Procedure Geometry Remove parentheses and subtract 360 from both sides: –2∠mjp –2∠ojm = –180. divide through by –2:: ∠mjp ∠ojm = 90. 8. jp is a tangent to circle o and passes through p. jp is a tangent to o because it touches the circle at j and is at right angles to a radius at the contact point. (see tangent to a circle.). In euclidean plane geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior. tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs. since the tangent line to a circle at a point p is. How to construct a tangent to point on circle. using just a compass and a straightedge. geometric constructions. Tangent is a line and to write the equation of a line we need two things, slope (m) and a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1.

Comments are closed.