Congruent Triangles Definition Properties Proof Examples
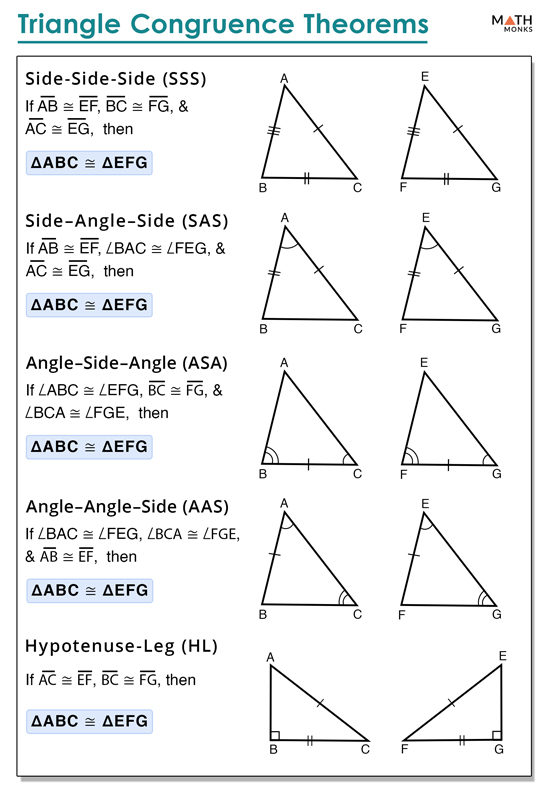
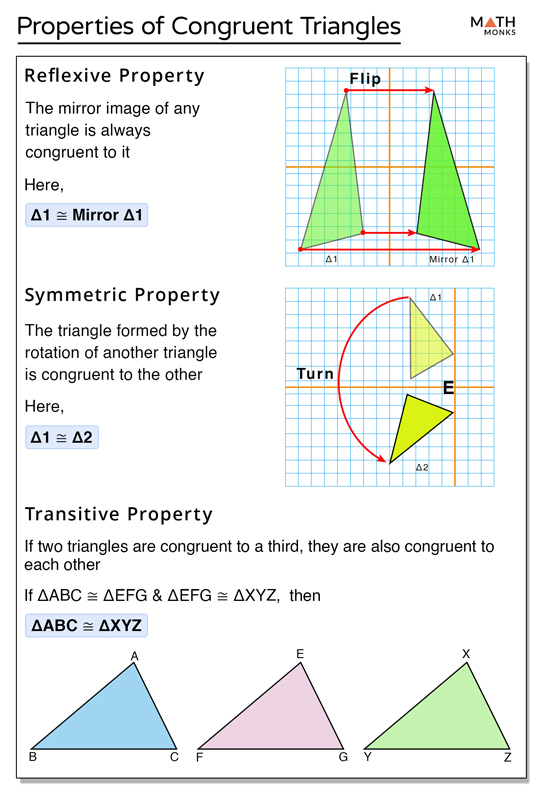
Congruent Triangles Definition Properties Proof Examples It means, one triangle can be congruent to the other although their equal sides and angles are not in the same position. properties of congruent triangles reflection rotation translation. 1) reflexive property. it states that the mirror image of any triangle is always congruent to it. 2) symmetric property. Angle side angle is a rule used to prove whether a given set of triangles are congruent. the aas rule states that: if two angles and a non included side of one triangle are equal to two angles and a non included side of another triangle, then the triangles are congruent. in the diagrams below, if ac = qp, angle a = angle q, and angle b = angle.
Congruent Triangles Definition Properties Proof Examples Cpctc – definition, proof, and examples. within the realm of geometry, a remarkable principle known as corresponding parts of congruent triangles is congruent (cpctc) unveils a hidden symmetry at the heart of triangle congruence. cpctc is a powerful tool, illuminating the profound relationship between congruent triangles and their. Example 1: recognize congruent triangles. decide whether this pair of triangles are congruent. if they are congruent, state why: check the corresponding angles and corresponding sides. both triangles have sides 5~ {cm} 5 cm and 7~ {cm}. 7 cm. they both have an angle of 95^ {\circ}. 95∘. 2 decide if the polygons are congruent or not. Proving triangles congruent. there are five theorems that can be used to show that two triangles are congruent. side side side (sss) theorem: for this theorem, all three sides of one triangle must. The three sides of a triangle determine its size and the three angles of a triangle determine its shape. two triangles are said to be congruent if pairs of their corresponding sides and their corresponding angles are equal. they are of the same shape and size. there are many conditions of congruence in triangles. let us discuss them in detail. 1.
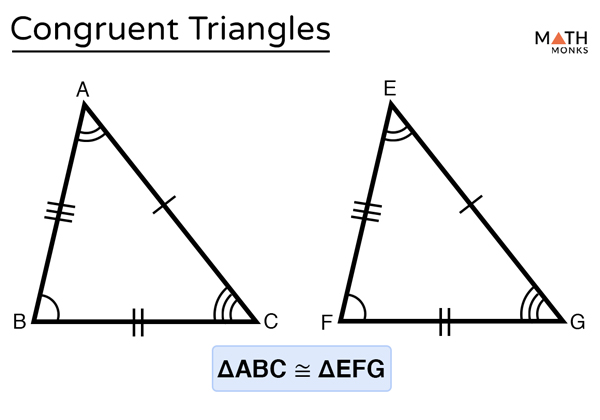
Congruent Triangles Definition Properties Proof Examples Proving triangles congruent. there are five theorems that can be used to show that two triangles are congruent. side side side (sss) theorem: for this theorem, all three sides of one triangle must. The three sides of a triangle determine its size and the three angles of a triangle determine its shape. two triangles are said to be congruent if pairs of their corresponding sides and their corresponding angles are equal. they are of the same shape and size. there are many conditions of congruence in triangles. let us discuss them in detail. 1. Cpctc proof. once it is shown that two triangles are congruent using one of the above congruence methods, we also know that all corresponding parts of the congruent triangles are congruent (abbreviated cpctc). let’s consider an example: consider Δ d a b and Δ d c b in which b a = b c and a d = d c are given. now, let’s prove the cpctc. The isosceles definition tells you that . the altitude definition tells you that and that ∠bdc and ∠bda are right angles. the triangles share side . the sides you need are contained in Δabd and Δcbd. use "corresponding parts of congruent Δs are congruent". (use hl for the congruent triangles in this example.) see proof.
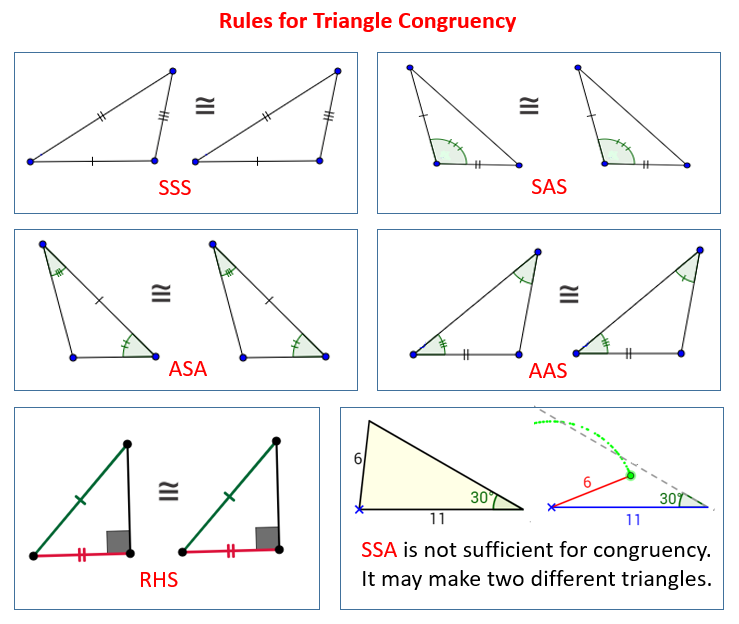
How To Prove Triangles Congruent Sss Sas Asa Aas Rules Solutions Cpctc proof. once it is shown that two triangles are congruent using one of the above congruence methods, we also know that all corresponding parts of the congruent triangles are congruent (abbreviated cpctc). let’s consider an example: consider Δ d a b and Δ d c b in which b a = b c and a d = d c are given. now, let’s prove the cpctc. The isosceles definition tells you that . the altitude definition tells you that and that ∠bdc and ∠bda are right angles. the triangles share side . the sides you need are contained in Δabd and Δcbd. use "corresponding parts of congruent Δs are congruent". (use hl for the congruent triangles in this example.) see proof.

How To Write A Congruent Triangles Geometry Proof 7 Steps

Comments are closed.