Complete A Piecewise Defined Function That Describes The Graph

Complete A Piecewise Defined Function That Describes The Graph Free piecewise functions calculator explore piecewise function domain, range, intercepts, extreme points and asymptotes step by step. A piecewise function is a function in which more than one formula is used to define the output over different pieces of the domain. we use piecewise functions to describe situations in which a rule or relationship changes as the input value crosses certain "boundaries." for example, we often encounter situations in business for which the cost.
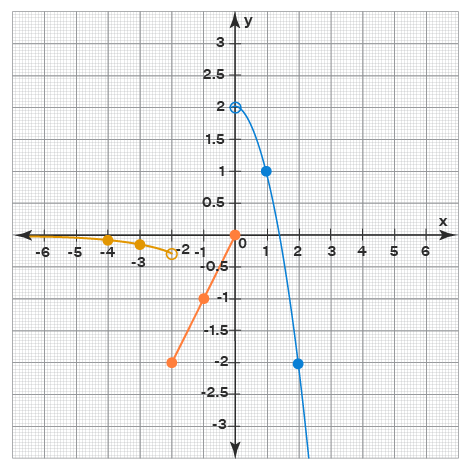
Complete A Piecewise Defined Function That Describes The Graph Answer to complete a piecewise defined function that describes. home > math 245 su 2021 (college algebra) > assessment practice problems 2.7 score: 20 25 24 25 answered question 25 < > the graph below is comprised of transformation of tool kit functions. Question: the graph below is comprised of transformation of tool kit functions.complete a piecewise defined function that describes the graph.f (x)= { if x<1 if x≥1. the graph below is comprised of transformation of tool kit functions. complete a piecewise defined function that describes the graph. there are 3 steps to solve this one. A piecewise function is a function that is defined in separate "pieces" or intervals. for each region or interval, the function may have a different equation or rule that describes it. we can graph a piecewise function by graphing each individual piece. A piecewise function is a function in which more than one formula is used to define the output. each formula has its own domain, and the domain of the function is the union of all these smaller domains. we notate this idea like this: f (x) =⎧⎨⎩formula 1 if x is in domain 1 formula 2 if x is in domain 2 formula 3 if x is in domain 3. in.
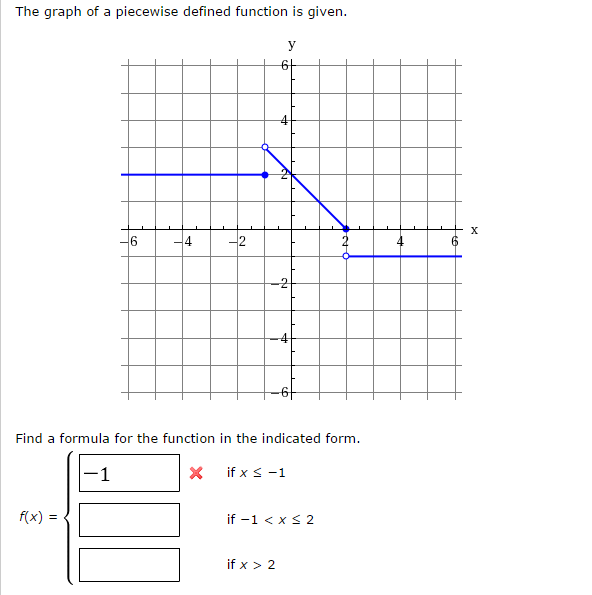
Complete A Piecewise Defined Function That Describes The Graph A piecewise function is a function that is defined in separate "pieces" or intervals. for each region or interval, the function may have a different equation or rule that describes it. we can graph a piecewise function by graphing each individual piece. A piecewise function is a function in which more than one formula is used to define the output. each formula has its own domain, and the domain of the function is the union of all these smaller domains. we notate this idea like this: f (x) =⎧⎨⎩formula 1 if x is in domain 1 formula 2 if x is in domain 2 formula 3 if x is in domain 3. in. To graph a piecewise function, you graph each piece on its domain. let’s start by graphing the piece with function x^2 and domain x<3, which is (part of) a parabola that opens upwards and has its vertex at the origin. the domain of the next piece is just , and we’re given that f (3)=8, so we’ll plot the point (3,8). Example 3: sketch the graph of the piecewise defined function . keep in mind that even though the second piece of the function (2 2) has the domain −2< ≤2 (which means that −2 is not part of the domain) we still need to plug −2 into 2 2 in order to get the complete graph of that piece of the function. if we started graphing that piece.
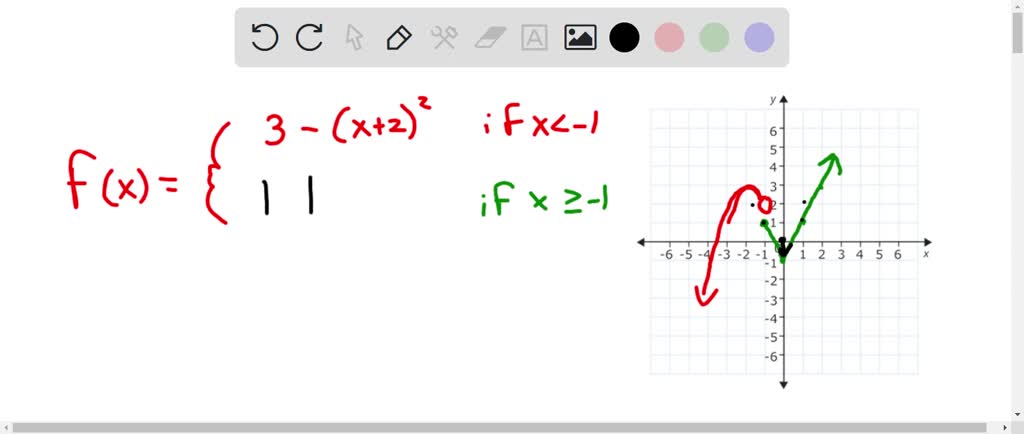
Solved The Graph Below Is Comprised Of Transformation Of Tool Kit To graph a piecewise function, you graph each piece on its domain. let’s start by graphing the piece with function x^2 and domain x<3, which is (part of) a parabola that opens upwards and has its vertex at the origin. the domain of the next piece is just , and we’re given that f (3)=8, so we’ll plot the point (3,8). Example 3: sketch the graph of the piecewise defined function . keep in mind that even though the second piece of the function (2 2) has the domain −2< ≤2 (which means that −2 is not part of the domain) we still need to plug −2 into 2 2 in order to get the complete graph of that piece of the function. if we started graphing that piece.
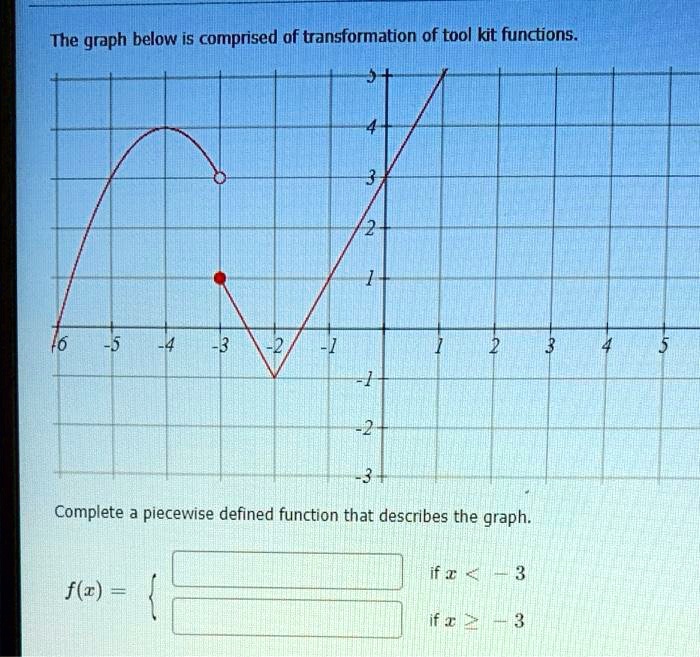
Solved The Graph Below Is Comprised Of Transformation Of Tool Kit

Comments are closed.