Common Tangents To Two Circles Geometry
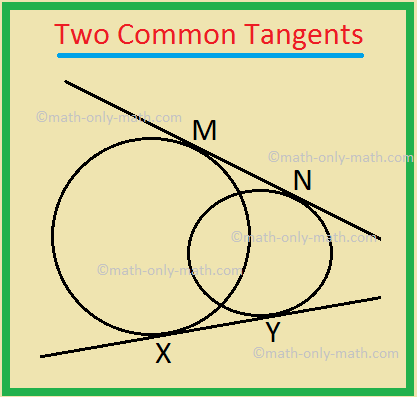
Common Tangents To Two Circles Transverse Common Tangents $\begingroup$ there are, in general, four common tangents to two circles, so you would expect to have four solutions. i would draw a diagram and use some geometry because these two circles seem to touch, and the tangent at that point will be perpendicular to the line joining the two centres. The figure below is the final construction with the line pj added. the construction has three main steps: the circle ojs is constructed so its radius is the difference between the radii of the two given circles. this means that jl = fp. we construct the tangent pj from the point p to the circle ojs. this is done using the method described in.

Common Tangents To Two Circles Geometry Youtube A common tangent is called transverse if the two circles lie on opposite sides of it. in the following situation, we have two circles lying externally to each other, and exactly two transverse common tangents: for two circles touching each other externally, there will be exactly one transverse common tangent (and of course, two direct common. This video illustrates the different types of common tangents that can be exist to two circles. common tangents include direct common tangent and transverse. The described algorithm will also work in the case when one (or both) circles degenerate into points. thus, this algorithm can also be used to find tangents to a circle passing through a given point. the number of common tangents. the number of common tangents to two circles can be 0,1,2,3,4 and infinite. look at the images for different cases. Two tangent theorem: when two segments are drawn tangent to a circle from the same point outside the circle, the segments are equal in length. in the following diagram: if ab and ac are two tangents to a circle centered at o, then: the tangents to the circle from the external point a are equal, oa bisects the angle bac between the two tangents,.
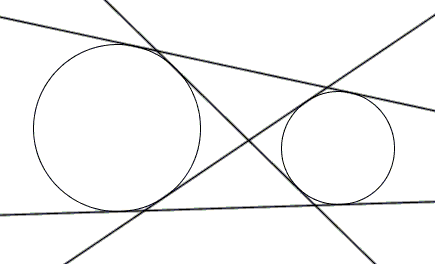
How To Construct Common Tangents To Two Circles The described algorithm will also work in the case when one (or both) circles degenerate into points. thus, this algorithm can also be used to find tangents to a circle passing through a given point. the number of common tangents. the number of common tangents to two circles can be 0,1,2,3,4 and infinite. look at the images for different cases. Two tangent theorem: when two segments are drawn tangent to a circle from the same point outside the circle, the segments are equal in length. in the following diagram: if ab and ac are two tangents to a circle centered at o, then: the tangents to the circle from the external point a are equal, oa bisects the angle bac between the two tangents,. Common tangent to two circles. let two circles having centers c1 c 1 and c2 c 2 and radii, r1 r 1 and r2 r 2 and c1 c 1 c2 c 2 is the distance between their centres then : (a) both circles will touch : (i) externally : if c1 c 1 c2 c 2 = r1 r 1 r2 r 2 i.e, the distance between their centres is equal to sum of their radii and point p & t divides. Circles intersecting at two points. same here. we’ll use the method in the first case for the direct common tangents. circles touching each other internally. the tangent here is perpendicular to the line joining the centres, and passes through the point which divides c 1 c 2 in the ratio r 1: r 2 externally.

Comments are closed.