Common Laplace Transform Pairs

Common Laplace Transform Pairs Common laplace transform pairs. *all time domain functions are implicitly=0 for t<0 (i.e. they are multiplied by unit step, γ(t)). †u(t) is more commonly used for the step, but is also used for other things. γ(t) is chosen to avoid confusion (and because in the laplace domain it looks a little like a step function, Γ(s)). The laplace transform is a mathematical tool which converts the differential equations in time domain into algebraic equations in the frequency domain (or s domain). if x(t) is a time function, then the laplace transform of the function is defined as −. l[x(t)] = x(s) = ∫∞ − ∞x(t)e − stdt ⋅ ⋅ ⋅ (1).

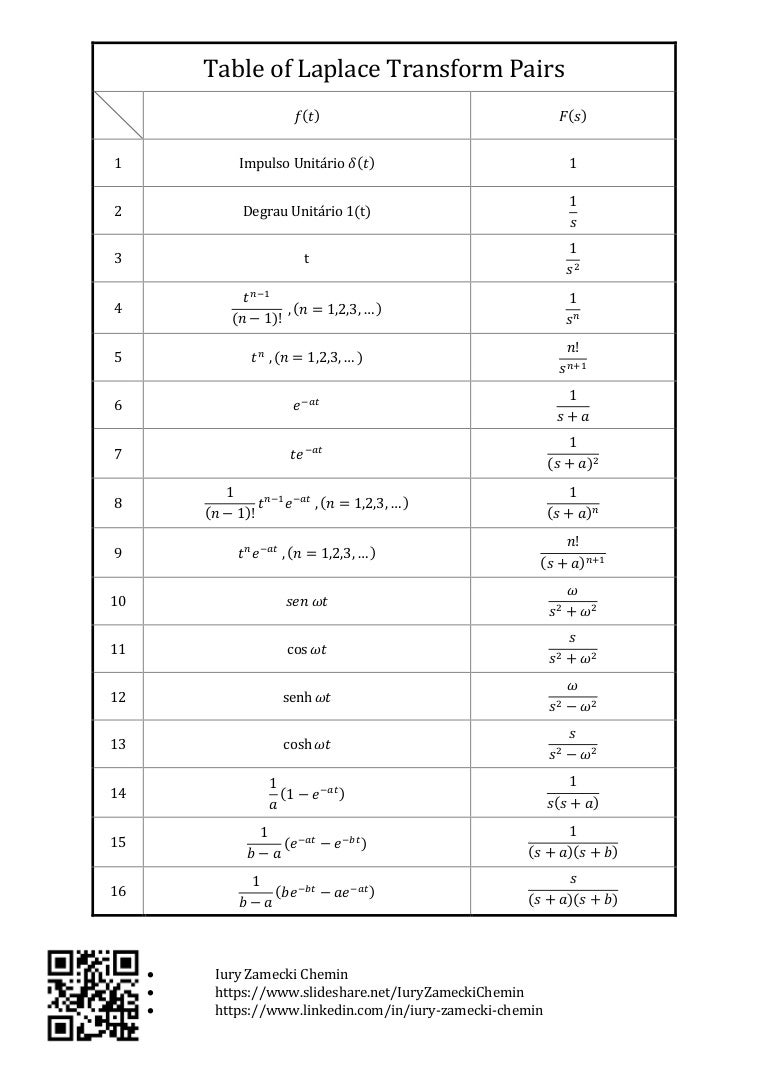
Table Of Laplace Transform Pairs 4. laplace transforms. 4.1 the definition; 4.2 laplace transforms; 4.3 inverse laplace transforms; 4.4 step functions; 4.5 solving ivp's with laplace transforms; 4.6 nonconstant coefficient ivp's; 4.7 ivp's with step functions; 4.8 dirac delta function; 4.9 convolution integrals; 4.10 table of laplace transforms; 5. systems of de's. 5.1 review. Common laplace transform pairs time domain function name definition* laplace domain function unit impulse δt( ) 1 unit step u t ( ) s 1 unit ramp t 2 1 s exponential e−at s a. A.3 common laplace transform pairs and properties the next three subsections present tables of common laplace transform pairs and laplace transform prop erties. the information in these tables has been adapted from: • signals and systems, 2nd ed. simon haykin and barry van veen. john wiley & sons, hoboken, nj, 2005. pp. 781 783. It is worthy of note that matlab’s symbolic software, which is introduced in homework problem 1.6, can sometimes be helpful for finding forward and inverse laplace transforms by applying, respectively, the laplace and ilaplace commands. the following are two relatively simple examples that do not appear explicitly in the table of transform pairs.

H6104 Formulae Sheet H6104 Common Laplace Transform Pairs Transient A.3 common laplace transform pairs and properties the next three subsections present tables of common laplace transform pairs and laplace transform prop erties. the information in these tables has been adapted from: • signals and systems, 2nd ed. simon haykin and barry van veen. john wiley & sons, hoboken, nj, 2005. pp. 781 783. It is worthy of note that matlab’s symbolic software, which is introduced in homework problem 1.6, can sometimes be helpful for finding forward and inverse laplace transforms by applying, respectively, the laplace and ilaplace commands. the following are two relatively simple examples that do not appear explicitly in the table of transform pairs. Laplace transforms 183 combining some of these simple laplace transforms with the properties of the laplace transform, as shown in table 5.3, we can deal with many ap plications of the laplace transform. we will first prove a few of the given laplace transforms and show how they can be used to obtain new trans form pairs. Summarized in table 4.1, and the table of common laplace transform pairs, table 4.2. the use of the partial fraction expansion method is sufficient for the purpose of this course. however, in general, in order to find the laplace transform of any laplace transformable function we must learn the complex variable integration and.

Solution Common Laplace Transform Pairs Studypool Laplace transforms 183 combining some of these simple laplace transforms with the properties of the laplace transform, as shown in table 5.3, we can deal with many ap plications of the laplace transform. we will first prove a few of the given laplace transforms and show how they can be used to obtain new trans form pairs. Summarized in table 4.1, and the table of common laplace transform pairs, table 4.2. the use of the partial fraction expansion method is sufficient for the purpose of this course. however, in general, in order to find the laplace transform of any laplace transformable function we must learn the complex variable integration and.

Basic Laplace Transform Table

Common Laplace Transform Pairs