Circle Theorems Involving Angle Measures Inscribed Angles Intersecting Chords Secants Tangents

Intersecting Secants Theorem Explained W 15 Examples Learn how to find various angles when working with circles in this free math video tutorial by mario's math tutoring. we discuss central angles, inscribed an. The formula. the angle formed by the intersection of 2 tangents, 2 secants or 1 tangent and 1 secant outside the circle equals half the difference of the intercepted arcs! therefore to find this angle (angle k in the examples below), all that you have to do is take the far intercepted arc and near the smaller intercepted arc and then divide.

Intersecting Secants Theorem Explained W 15 Examples Finding a circle's center. we can use this idea to find a circle's center: draw a right angle from anywhere on the circle's circumference, then draw the diameter where the two legs hit the circle; do that again but for a different diameter; where the diameters cross is the center! drawing a circle from 2 opposite points. We start by saying that the angle subtended by arc cd at o is 2θ and the arc subtended by arc ab at o is 2Φ. by the angle at the center theorem: ∠dac = ∠dbc = θ and ∠adb = ∠acb = Φ. and pac is 180°, so: ∠dap = 180° − θ. now use angles of a triangle add to 180° in triangle apd: ∠cpd = 180° − (∠dap ∠adp). In the case of a pentagon, the interior angles have a measure of (5 2) •180 5 = 108 °. therefore, each inscribed angle creates an arc of 216° use the inscribed angle formula and the formula for the angle of a tangent and a secant to arrive at the angles. The measure of an angle inscribed in a circle is equal to one half the measure of its intercepted arc. these results can be applied to both numerical and algebraic problems to calculate the measures of angles resulting from the intersection of two chords, two secants, two tangents, or a tangent and a secant in a circle.

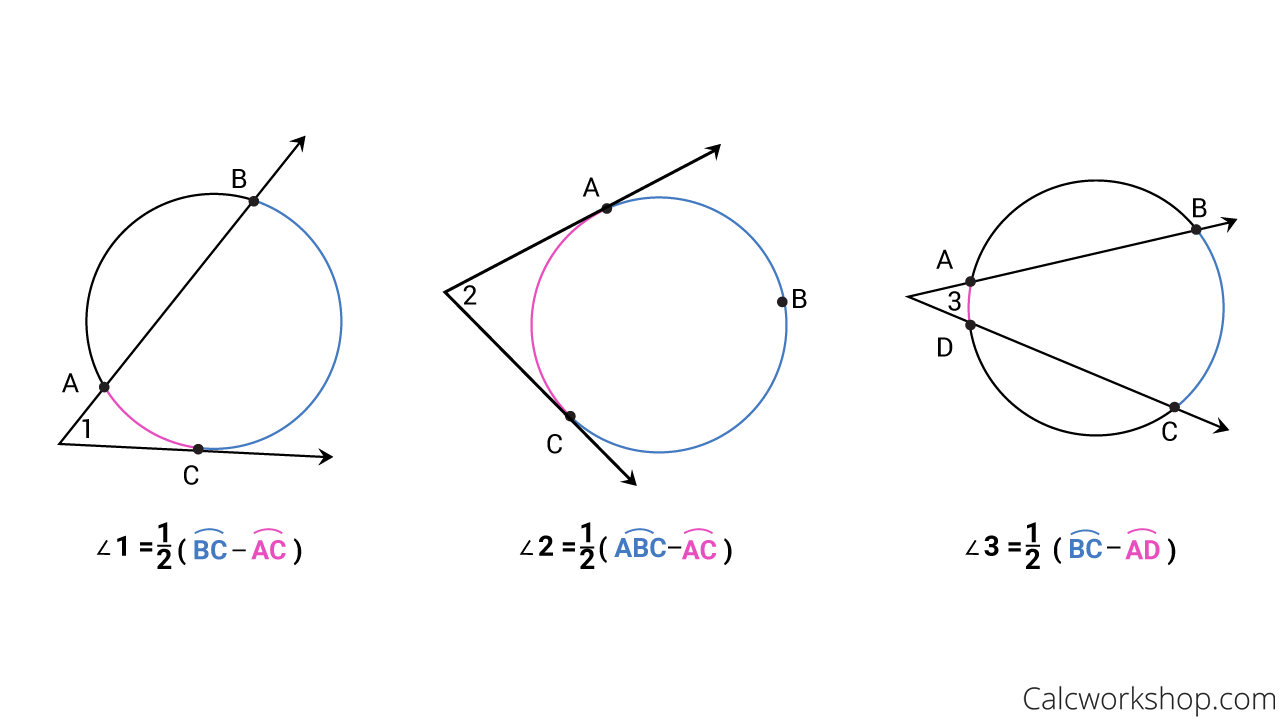
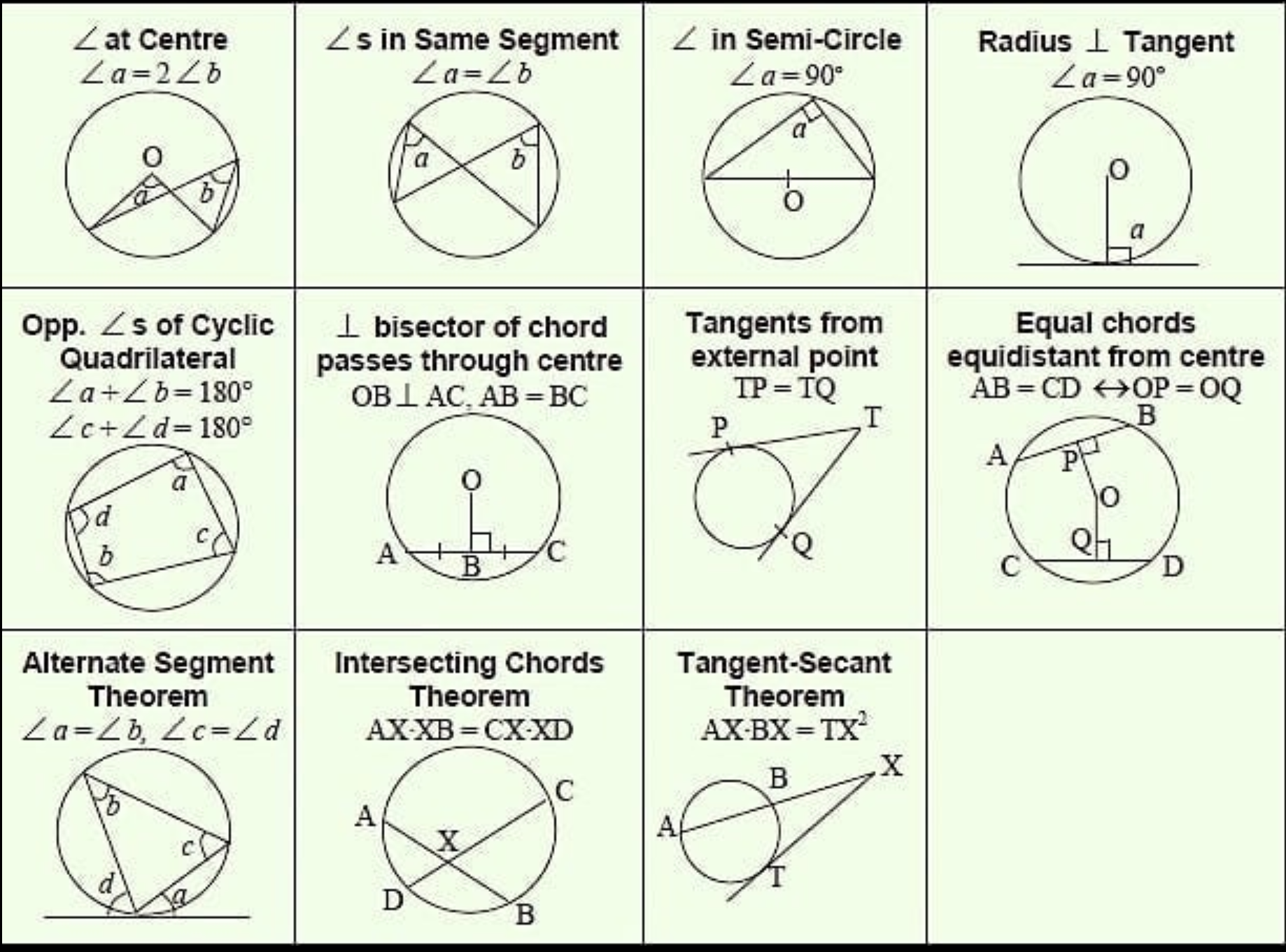
Intersecting Secants Theorem Explained W 15 Examples In the case of a pentagon, the interior angles have a measure of (5 2) •180 5 = 108 °. therefore, each inscribed angle creates an arc of 216° use the inscribed angle formula and the formula for the angle of a tangent and a secant to arrive at the angles. The measure of an angle inscribed in a circle is equal to one half the measure of its intercepted arc. these results can be applied to both numerical and algebraic problems to calculate the measures of angles resulting from the intersection of two chords, two secants, two tangents, or a tangent and a secant in a circle. The inscribed angle may intercept a minor arc, a major arc or a semicircle. t16 1 the measure of an inscribed angle is equal to half the measure of its intercepted arc. c16 1 if two inscribed angles intercept the same arc, then the angles are congruent. c16 2 if a quadrilateral is inscribed in a circle, then its opposite angles are. The diagram below shows what happens when tangents and secants intersect on a circle. you get inscribed angles and arcs! therefore, the measure of inscribed angle 1 is equal to one half of the measure its intercepted arc acb. likewise, the measure of inscribed angle 2 is equal to one half its intercepted arc ab. tangent chord angles.

Angles And Tangents Of Circles The inscribed angle may intercept a minor arc, a major arc or a semicircle. t16 1 the measure of an inscribed angle is equal to half the measure of its intercepted arc. c16 1 if two inscribed angles intercept the same arc, then the angles are congruent. c16 2 if a quadrilateral is inscribed in a circle, then its opposite angles are. The diagram below shows what happens when tangents and secants intersect on a circle. you get inscribed angles and arcs! therefore, the measure of inscribed angle 1 is equal to one half of the measure its intercepted arc acb. likewise, the measure of inscribed angle 2 is equal to one half its intercepted arc ab. tangent chord angles.

Angles Circle Tangent Chord Intersecting Chords Worksheet 1 Answers