Circle Theorems 12 Angles And Arcs Shorts
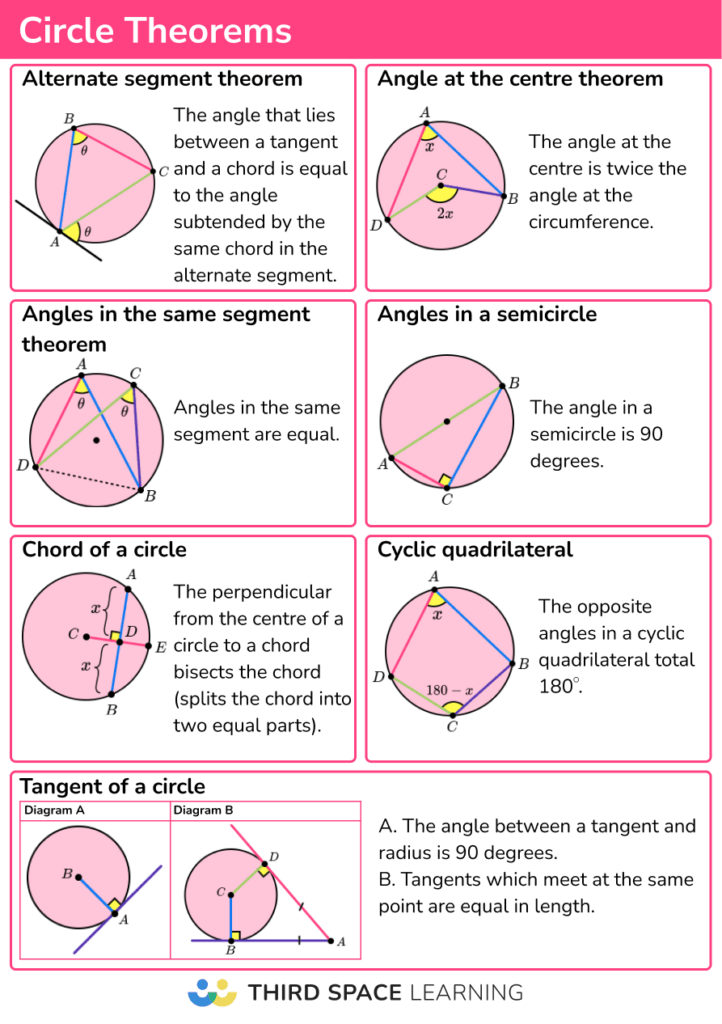
Circle Theorems Gcse Maths Steps Examples Worksheet Finding a circle's center. we can use this idea to find a circle's center: draw a right angle from anywhere on the circle's circumference, then draw the diameter where the two legs hit the circle; do that again but for a different diameter; where the diameters cross is the center! drawing a circle from 2 opposite points. Example 2: consider the circle given below with center o. find the angle x using the circle theorems. solution: using the circle theorem 'the angle subtended by the diameter at the circumference is a right angle.', we have ∠abc = 90°. so, using the triangle sum theorem, ∠bac ∠acb ∠abc = 180°.

Circle Theorems Notes Corbettmaths Solved examples on circle theorems. in the circle given below, triangle abc is inscribed in the circle and the tangent de meets the circle at the point b. find the measure of angle “x” and “y.”. solution: we know that the sum of interior angles of a triangle is equal to 180. ∠bac ∠acb ∠abc = 1800. Example 5: chord of a circle (cosine ratio) below is a circle with centre c. points a, b, c, and d are on the circumference of the circle. the chord ab is perpendicular to the line cd at the point e. the line ae is 5cm 5cm and angle ade =71o = 71o. calculate the length of the line bc correct to 1 1 decimal place. The opposite angles of such a quadrilateral add up to 180 degrees. area of sector and arc length. if the radius of the circle is r, area of sector = πr 2 × a 360. arc length = 2πr × a 360. in other words, area of sector = area of circle × a 360. arc length = circumference of circle × a 360. The central angle of a circle is twice any inscribed angle subtended by the same arc. angle inscribed in semicircle is 90°. an angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment. the opposite angles of a cyclic quadrilateral are supplementary.
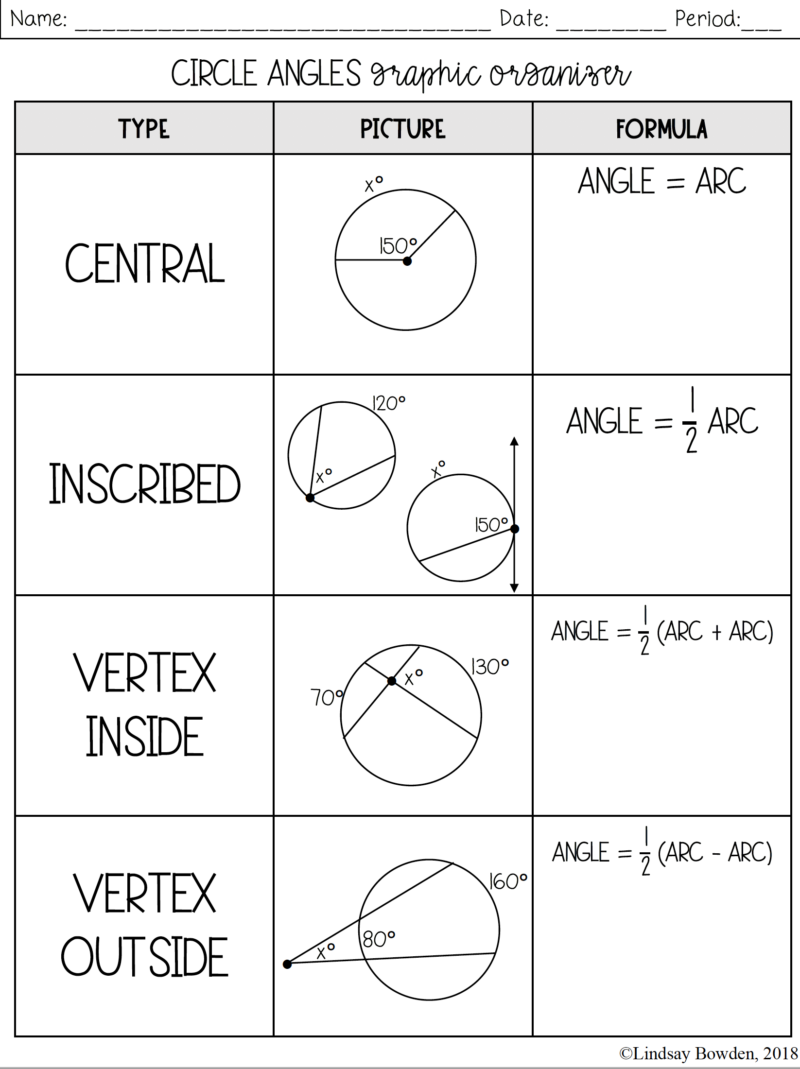
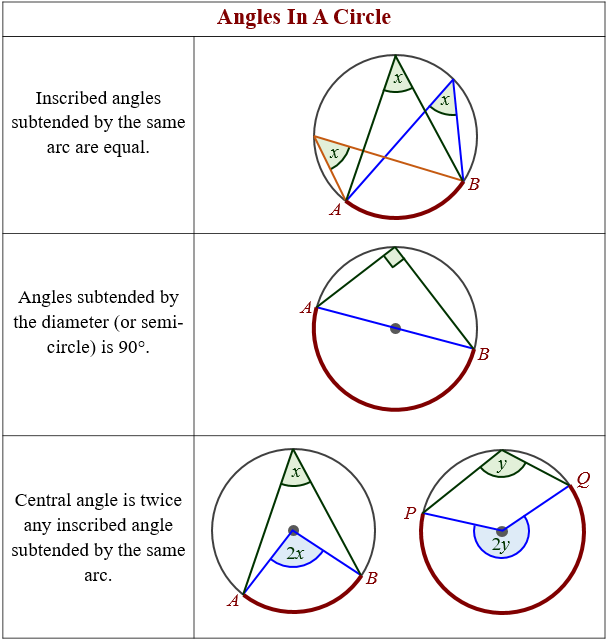
Circle Theorems Graphic Organizer Lindsay Bowden The opposite angles of such a quadrilateral add up to 180 degrees. area of sector and arc length. if the radius of the circle is r, area of sector = πr 2 × a 360. arc length = 2πr × a 360. in other words, area of sector = area of circle × a 360. arc length = circumference of circle × a 360. The central angle of a circle is twice any inscribed angle subtended by the same arc. angle inscribed in semicircle is 90°. an angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment. the opposite angles of a cyclic quadrilateral are supplementary. Solution: ∠ x = 38˚ because they are both subtended by the same arc prq. (1) inscribed angles from equal arcs are equal. (2) arcs that contain equal angles are equal. (1) the measure of the inscribed angle is half the measure of the central angle. (2) inscribed angles that intercept congruent arcs are congruent. The angle at the centre of a circle is twice any angle at the circumference subtended by the same arc. the following diagrams illustrates the inscribed angle theorem. example: the center of the following circle is o. bod is a diameter of the circle. find the value of x. solution: ∠boc 70˚ = 180˚.

Circles Angles And Arcs Worksheets Solution: ∠ x = 38˚ because they are both subtended by the same arc prq. (1) inscribed angles from equal arcs are equal. (2) arcs that contain equal angles are equal. (1) the measure of the inscribed angle is half the measure of the central angle. (2) inscribed angles that intercept congruent arcs are congruent. The angle at the centre of a circle is twice any angle at the circumference subtended by the same arc. the following diagrams illustrates the inscribed angle theorem. example: the center of the following circle is o. bod is a diameter of the circle. find the value of x. solution: ∠boc 70˚ = 180˚.
Angles And Arcs In Circles Worksheet

Comments are closed.