Circle Theorem 8 Proof Alternate Segment Theorem Circletheorem Mathinar

Alternate Segment Theorem Circles Proof Solutions Cuemath Assume that ∠acb = ∠β is the alternate angle in the alternate segment for the angle between the tangent a and the chord ab. proof: let a be the point on the circumference of the circle, and “o” be the centre of the circle. assume that pq is the tangent of the circle that passes through point a. the tangent makes an angle α with the. Alternate segment theorem. the segment of a circle is the region between a chord and the corresponding arc of the circle. when a chord is drawn, it creates a major segment and a minor segment in the circle. let's observe the figure given below, in which de is the tangent and bc is a chord. ∠ ∠ bce is made by the tangent and chord bc.

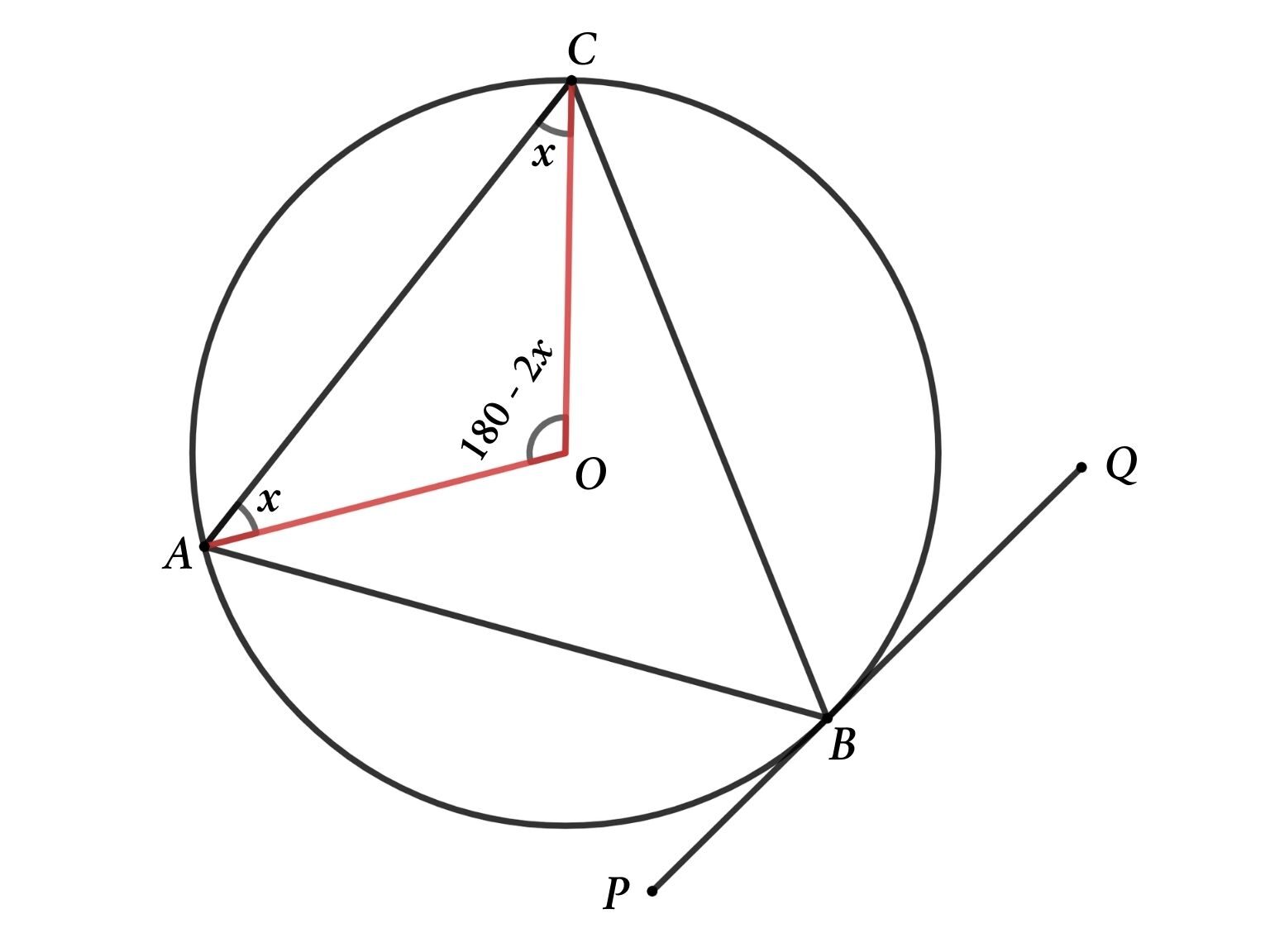
Alternate Segment Theorem In A Circle Educate Math The alternate segment theorem higher solving problems using circle theorems higher the angle between a tangent close tangent a straight line that just touches a point on a curve. Alternate segment theorem the shaded segment is called the alternate segment in relation to ∠stq. the unshaded segment is alternate to ∠pts p t q s theorem 7 the angle between a tangent and a chord drawn from the point of contact is equal to any angle in the alternate segment. proof let ∠stq = x ,∠rts = y and ∠trs = z where rt is a. The alternate segment theorem states. an angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment. recall that a chord is any straight line drawn across a circle, beginning and ending on the curve of the circle. in the following diagram, the chord ce divides the circle into 2 segments. This theorem is proved using the circle theorem "an angle subtended at the centre of a circle is twice the angle subtended at the circumference of a circle". step 1. draw the radii from the centre of the circle to any two of the vertices of the cyclic quadrilateral that are opposite each other.

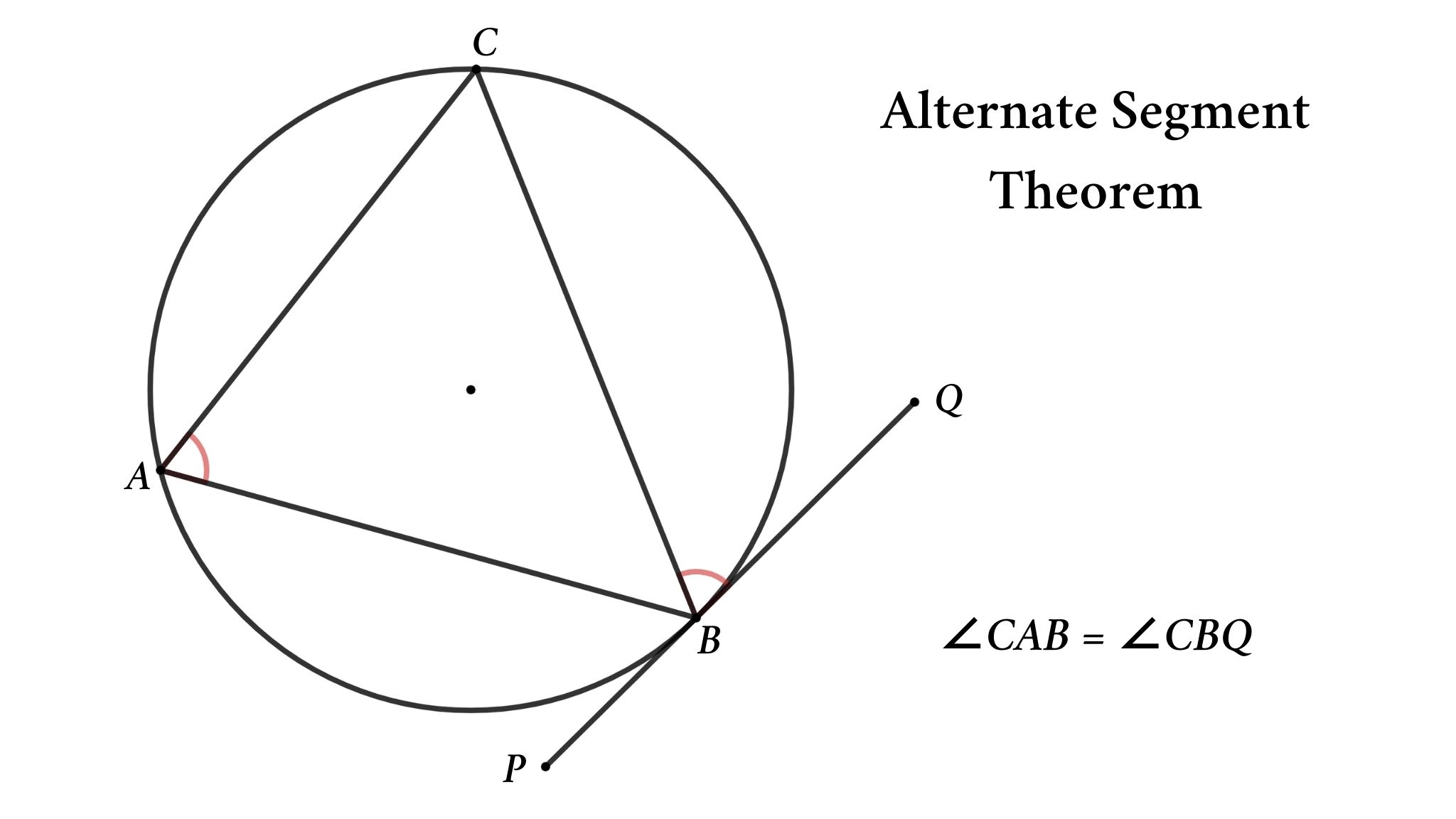
Alternate Segment Theorem In A Circle Educate Math The alternate segment theorem states. an angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment. recall that a chord is any straight line drawn across a circle, beginning and ending on the curve of the circle. in the following diagram, the chord ce divides the circle into 2 segments. This theorem is proved using the circle theorem "an angle subtended at the centre of a circle is twice the angle subtended at the circumference of a circle". step 1. draw the radii from the centre of the circle to any two of the vertices of the cyclic quadrilateral that are opposite each other. Alternate segment theorem. here we will learn about the alternate segment theorem, including their application, proof, and using them to solve more difficult problems. there are also circle theorem worksheets based on edexcel, aqa and ocr exam questions, along with further guidance on where to go next if you’re still stuck. The opposite angles of such a quadrilateral add up to 180 degrees. area of sector and arc length. if the radius of the circle is r, area of sector = πr 2 × a 360. arc length = 2πr × a 360. in other words, area of sector = area of circle × a 360. arc length = circumference of circle × a 360.

Circle Theorem 8 Proof Alternate Segment Theorem Circletheorem Alternate segment theorem. here we will learn about the alternate segment theorem, including their application, proof, and using them to solve more difficult problems. there are also circle theorem worksheets based on edexcel, aqa and ocr exam questions, along with further guidance on where to go next if you’re still stuck. The opposite angles of such a quadrilateral add up to 180 degrees. area of sector and arc length. if the radius of the circle is r, area of sector = πr 2 × a 360. arc length = 2πr × a 360. in other words, area of sector = area of circle × a 360. arc length = circumference of circle × a 360.