Charles Jekel Jekel Me Maximum Likelihood Estimation Linear Regression

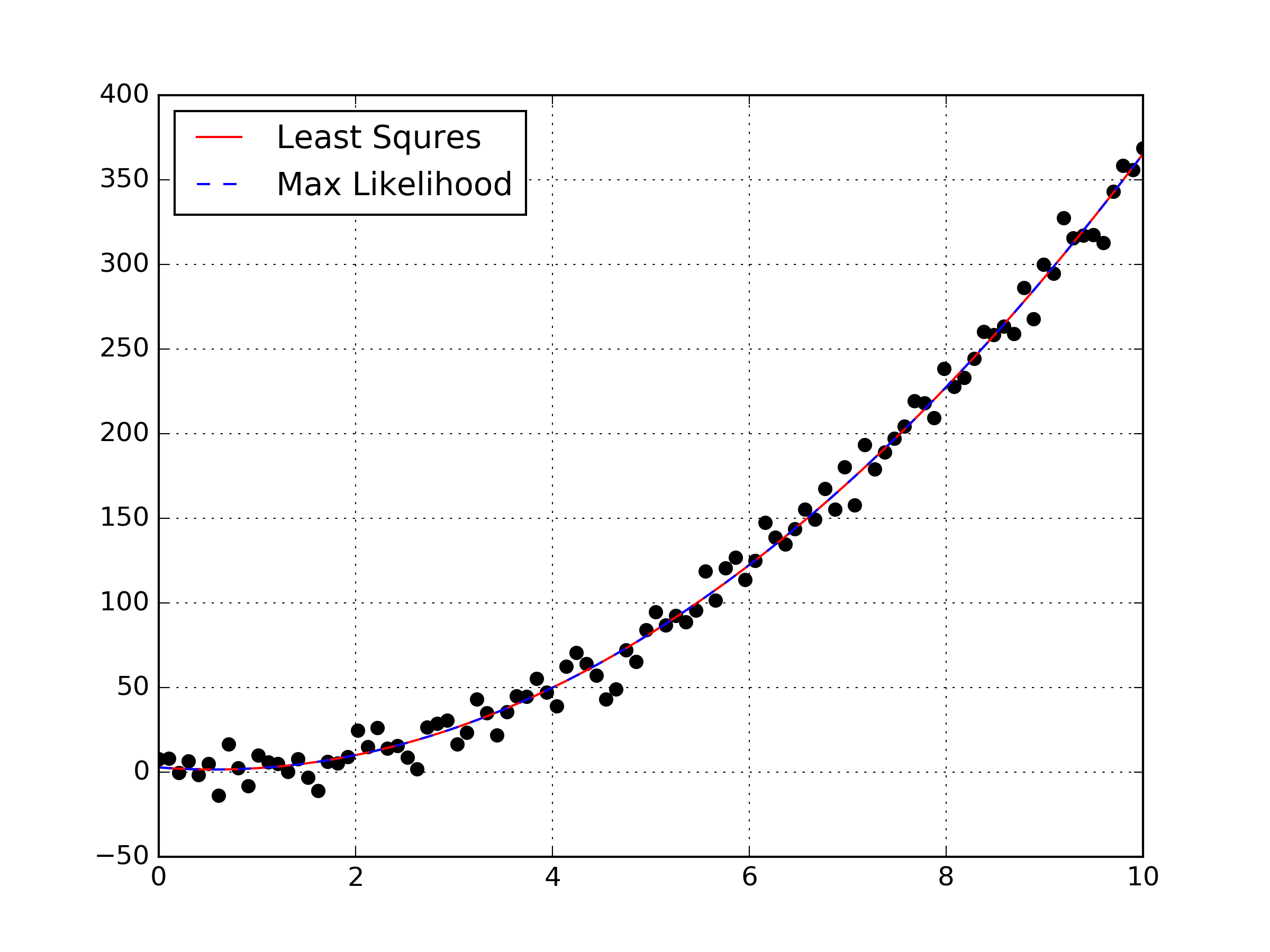
Charles Jekel Jekel Me Maximum Likelihood Estimation Linear Regression Linear regression is generally of some form. y = xβ r y = x β r. for a true function y y, the matrix of independent variables x x, the model coefficients β β, and some residual difference between the true data and the model r r. for a second order polynomial, x x is of the form x = [1,x,x2] x = [ 1, x, x 2]. Maximum likelihood estimation is sensitive to starting points october 21, 2016. in my previous post, i derive a formulation to use maximum likelihood estimation (mle) in a simple linear regression case. looking at the formulation for mle, i had the suspicion that the mle will be much more sensitive to the starting points of a gradient.

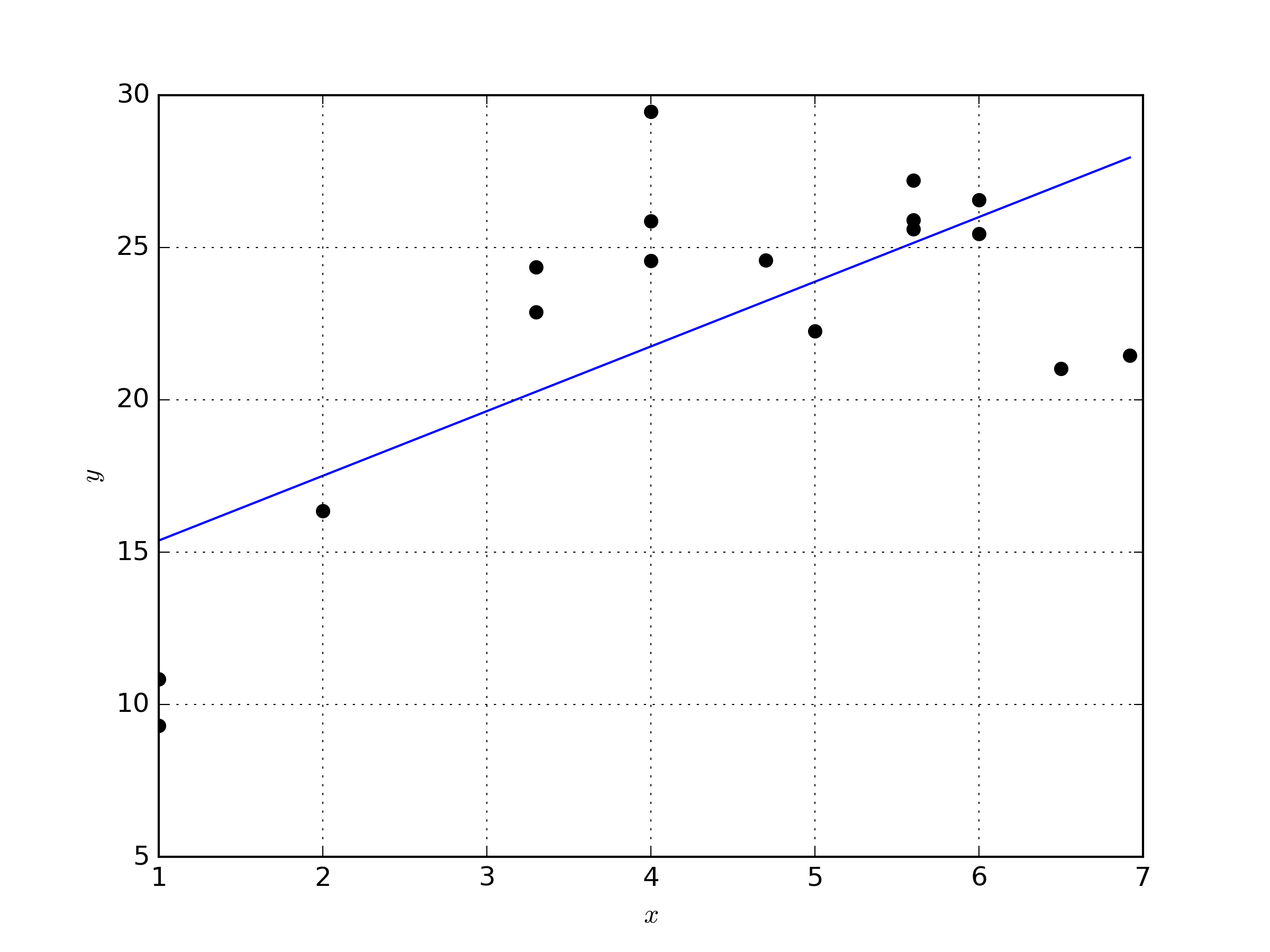
Charles Jekel Jekel Me Lack Of Fit Test For Linear Regression The first entries of the score vector are the th entry of the score vector is the hessian, that is, the matrix of second derivatives, can be written as a block matrix let us compute the blocks: and finally, therefore, the hessian is by the information equality, we have that but and, by the law of iterated expectations, thus, as a consequence, the asymptotic covariance matrix is. Index: the book of statistical proofs statistical models univariate normal data simple linear regression maximum likelihood estimation . theorem: given a simple linear regression model with independent observations \[\label{eq:slr} y i = \beta 0 \beta 1 x i \varepsilon i, \; \varepsilon i \sim \mathcal{n}(0, \sigma^2), \; i = 1,\ldots,n. This is a conditional probability density (cpd) model. linear regression can be written as a cpd in the following manner: p (y ∣ x, θ) = (y ∣ μ (x), σ 2 (x)) for linear regression we assume that μ (x) is linear and so μ (x) = β t x. we must also assume that the variance in the model is fixed (i.e. that it doesn't depend on x) and as. We introduced the method of maximum likelihood for simple linear regression in the notes for two lectures ago. let’s review. we start with the statistical model, which is the gaussian noise simple linear regression model, de ned as follows: 1.the distribution of xis arbitrary (and perhaps xis even non random). 2.if x = x, then y = 0.

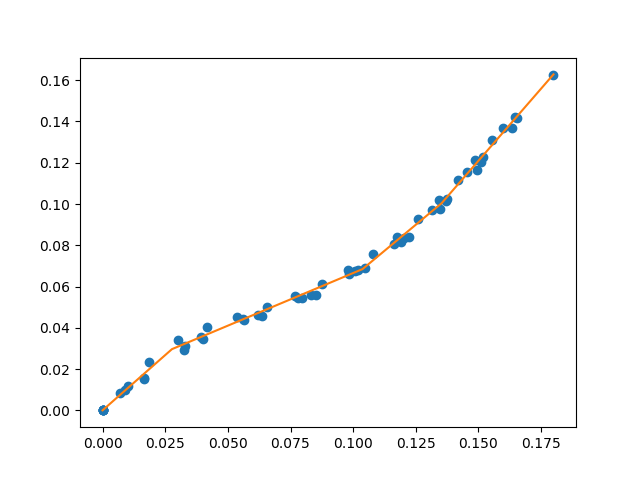
Charles Jekel Jekel Me Fitting A Piecewise Linear Function To Data This is a conditional probability density (cpd) model. linear regression can be written as a cpd in the following manner: p (y ∣ x, θ) = (y ∣ μ (x), σ 2 (x)) for linear regression we assume that μ (x) is linear and so μ (x) = β t x. we must also assume that the variance in the model is fixed (i.e. that it doesn't depend on x) and as. We introduced the method of maximum likelihood for simple linear regression in the notes for two lectures ago. let’s review. we start with the statistical model, which is the gaussian noise simple linear regression model, de ned as follows: 1.the distribution of xis arbitrary (and perhaps xis even non random). 2.if x = x, then y = 0. 16. ml is a higher set of estimators which includes least absolute deviations (l1 l 1 norm) and least squares (l2 l 2 norm). under the hood of ml the estimators share a wide range of common properties like the (sadly) non existent break point. in fact you can use the ml approach as a substitute to optimize a lot of things including ols as. Dec 04, 2021 ellipsoid non linear regression fitting how to fit an ellipsoid to data points using non linear regression. included is a simple python example using jax. sep 20, 2020 least squares ellipsoid fit how to fit an ellipsoid to data points using the least squares method with a simple python example.

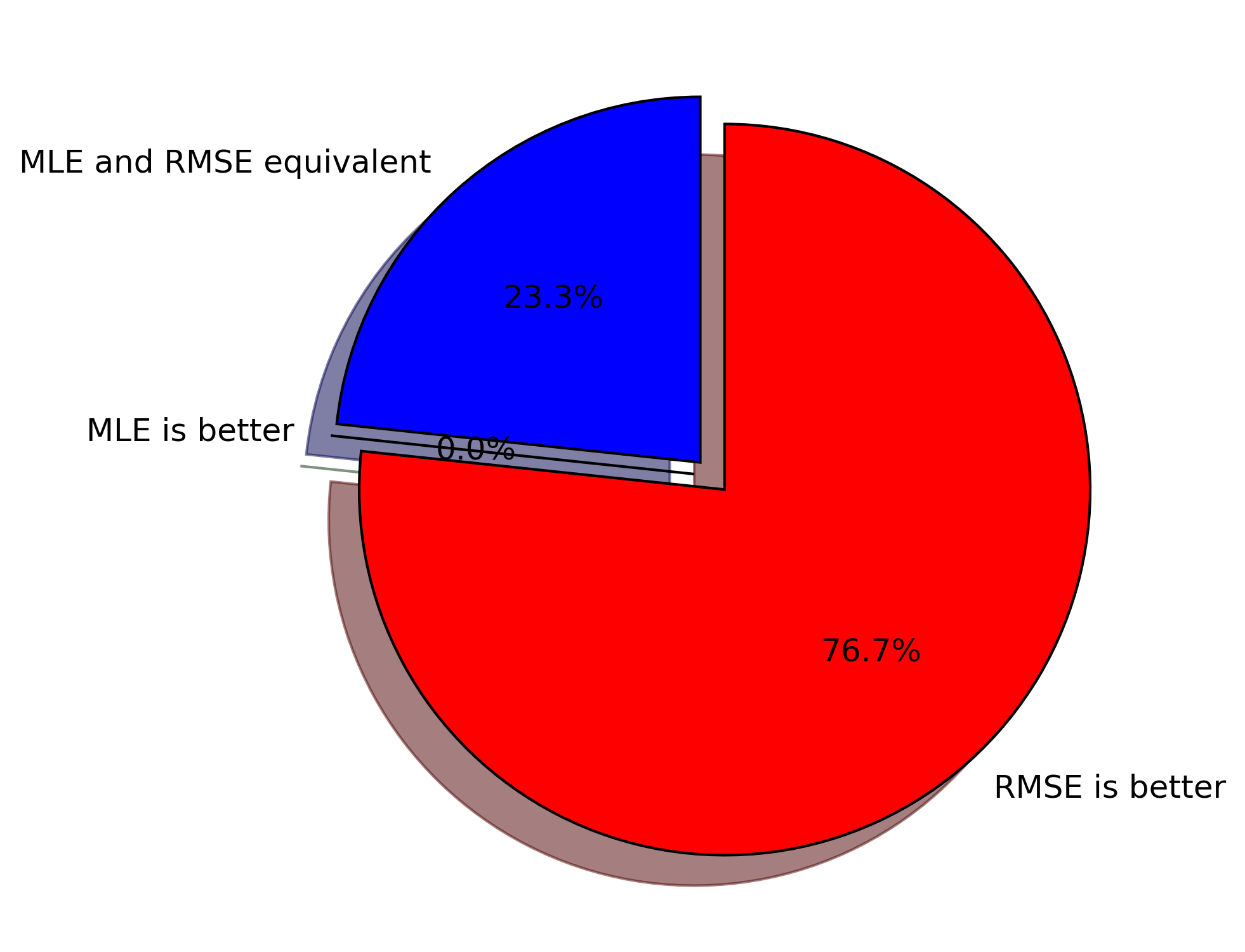
Charles Jekel Jekel Me Maximum Likelihood Estimation Is Sensitive 16. ml is a higher set of estimators which includes least absolute deviations (l1 l 1 norm) and least squares (l2 l 2 norm). under the hood of ml the estimators share a wide range of common properties like the (sadly) non existent break point. in fact you can use the ml approach as a substitute to optimize a lot of things including ols as. Dec 04, 2021 ellipsoid non linear regression fitting how to fit an ellipsoid to data points using non linear regression. included is a simple python example using jax. sep 20, 2020 least squares ellipsoid fit how to fit an ellipsoid to data points using the least squares method with a simple python example.