Characteristics Of Polynomial Functions With Graph
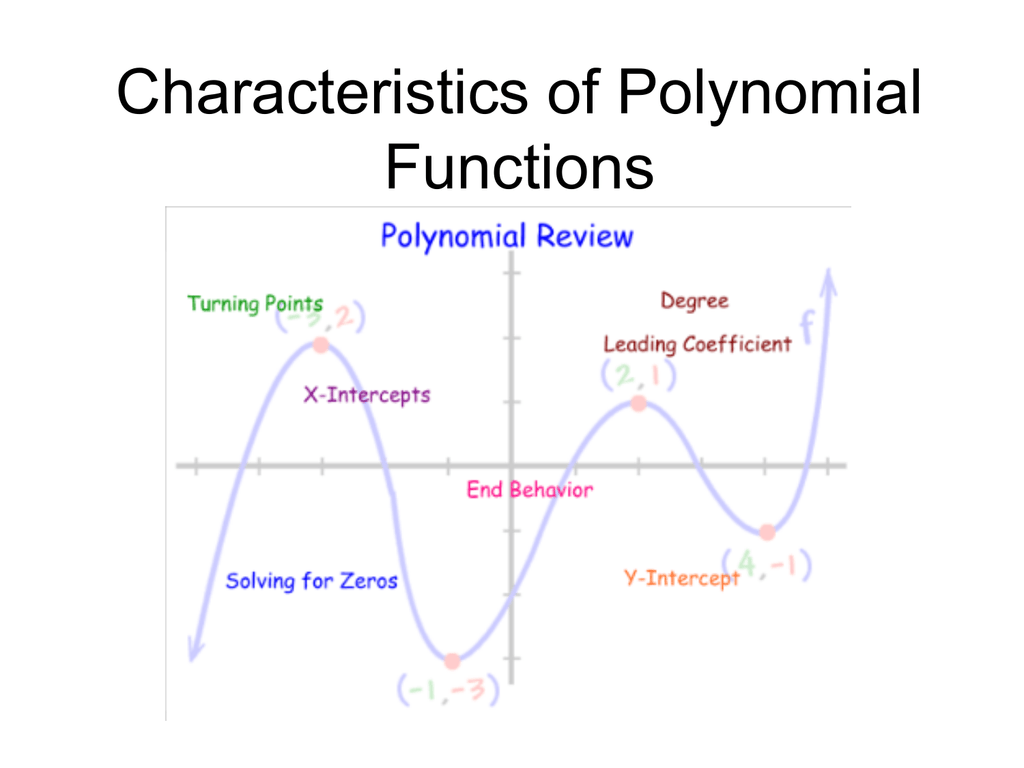
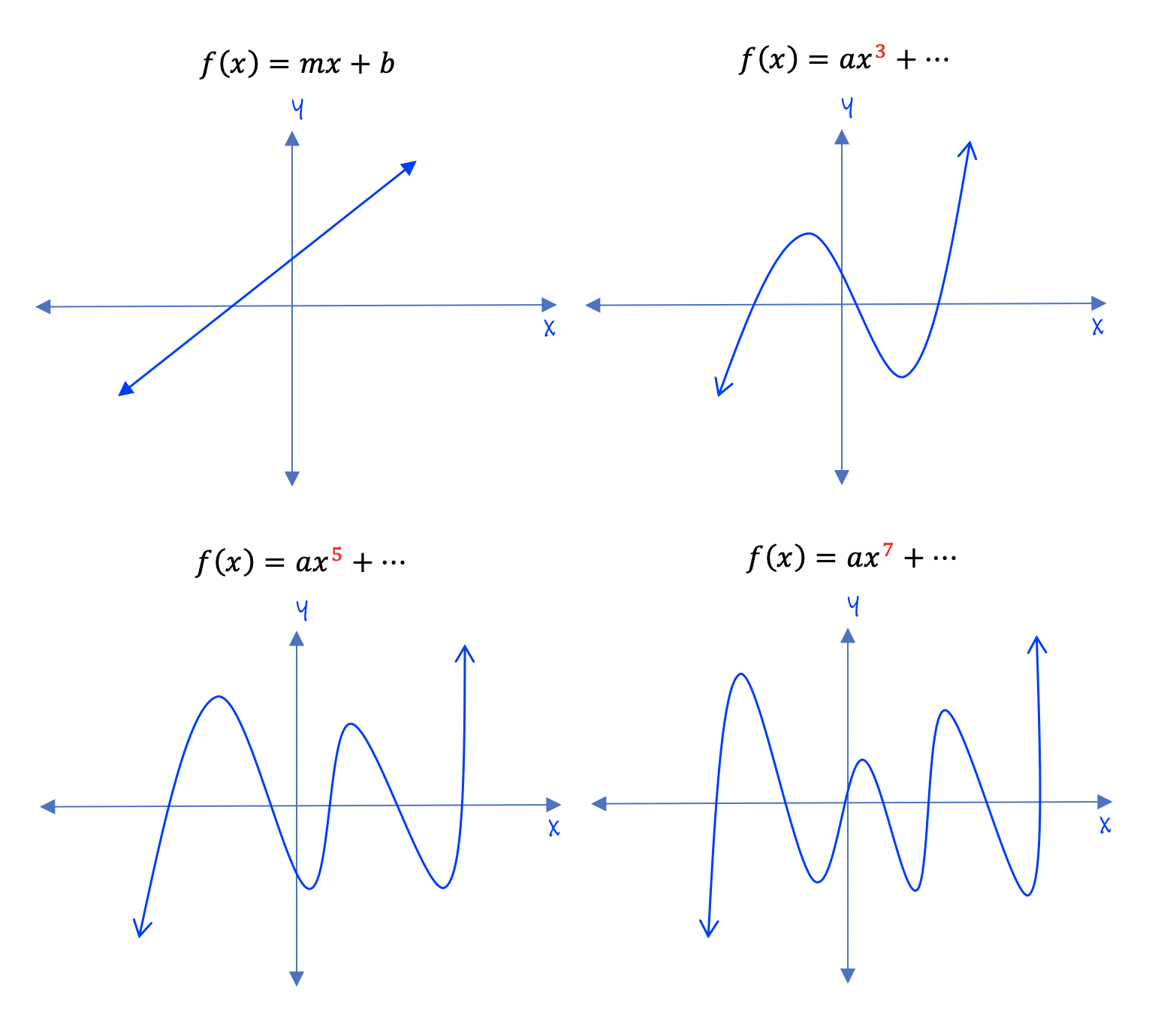
Characteristics Of Polynomial Functions Recognizing characteristics of graphs of polynomial functions. polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. polynomial functions also display graphs that have no breaks. curves with no breaks are called continuous. The graph of a polynomial will touch the horizontal axis at a zero with even multiplicity. the end behavior of a polynomial function depends on the leading term. the graph of a polynomial function changes direction at its turning points. a polynomial function of degree n has at most n − 1 turning points.
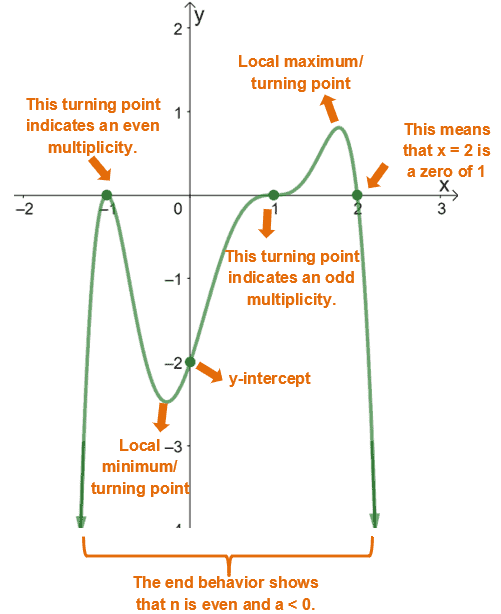
Polynomial Functions Properties Graphs And Examples Recognizing characteristics of graphs of polynomial functions. polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. polynomial functions also display graphs that have no breaks. curves with no breaks are called continuous. Recognizing characteristics of graphs of polynomial functions. polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. polynomial functions also display graphs that have no breaks. curves with no breaks are called continuous. The graph has three turning points. figure 4.4.12: graph of f(x) = x4 − x3 − 4x2 4x. this function f is a 4th degree polynomial function and has 3 turning points. the maximum number of turning points of a polynomial function is always one less than the degree of the function. About this unit. in this unit, we will use everything that we know about polynomials in order to analyze their graphical behavior. specifically, we will find polynomials' zeros (i.e., x intercepts) and analyze how they behave as the x values become infinitely positive or infinitely negative (i.e., end behavior).
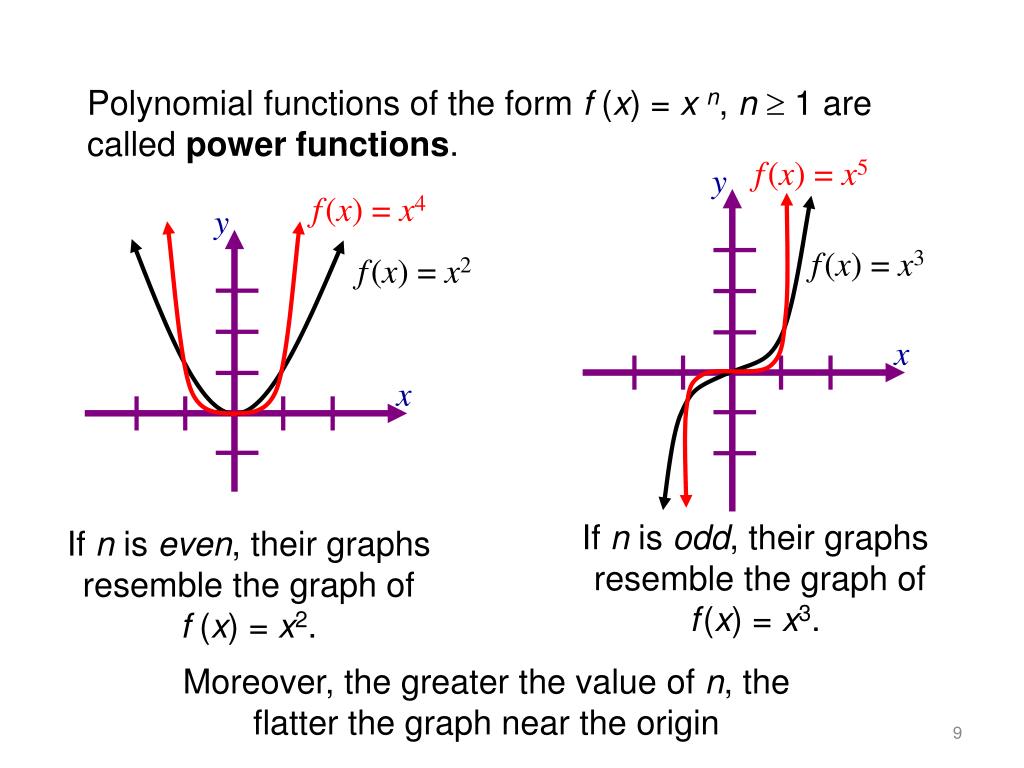
Ppt Graphs Of Polynomial Functions Powerpoint Presentation Free The graph has three turning points. figure 4.4.12: graph of f(x) = x4 − x3 − 4x2 4x. this function f is a 4th degree polynomial function and has 3 turning points. the maximum number of turning points of a polynomial function is always one less than the degree of the function. About this unit. in this unit, we will use everything that we know about polynomials in order to analyze their graphical behavior. specifically, we will find polynomials' zeros (i.e., x intercepts) and analyze how they behave as the x values become infinitely positive or infinitely negative (i.e., end behavior). Polynomial functions have all of these characteristics as well as a domain and range, and corresponding graphs. in this section we will identify and evaluate polynomial functions. because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable. The graph of a polynomial will touch and bounce off the x axis at a zero with even multiplicity. the end behavior of a polynomial function depends on the leading term. the graph of a polynomial function changes direction at its turning points. a polynomial function of degree n has at most n – 1 turning points.
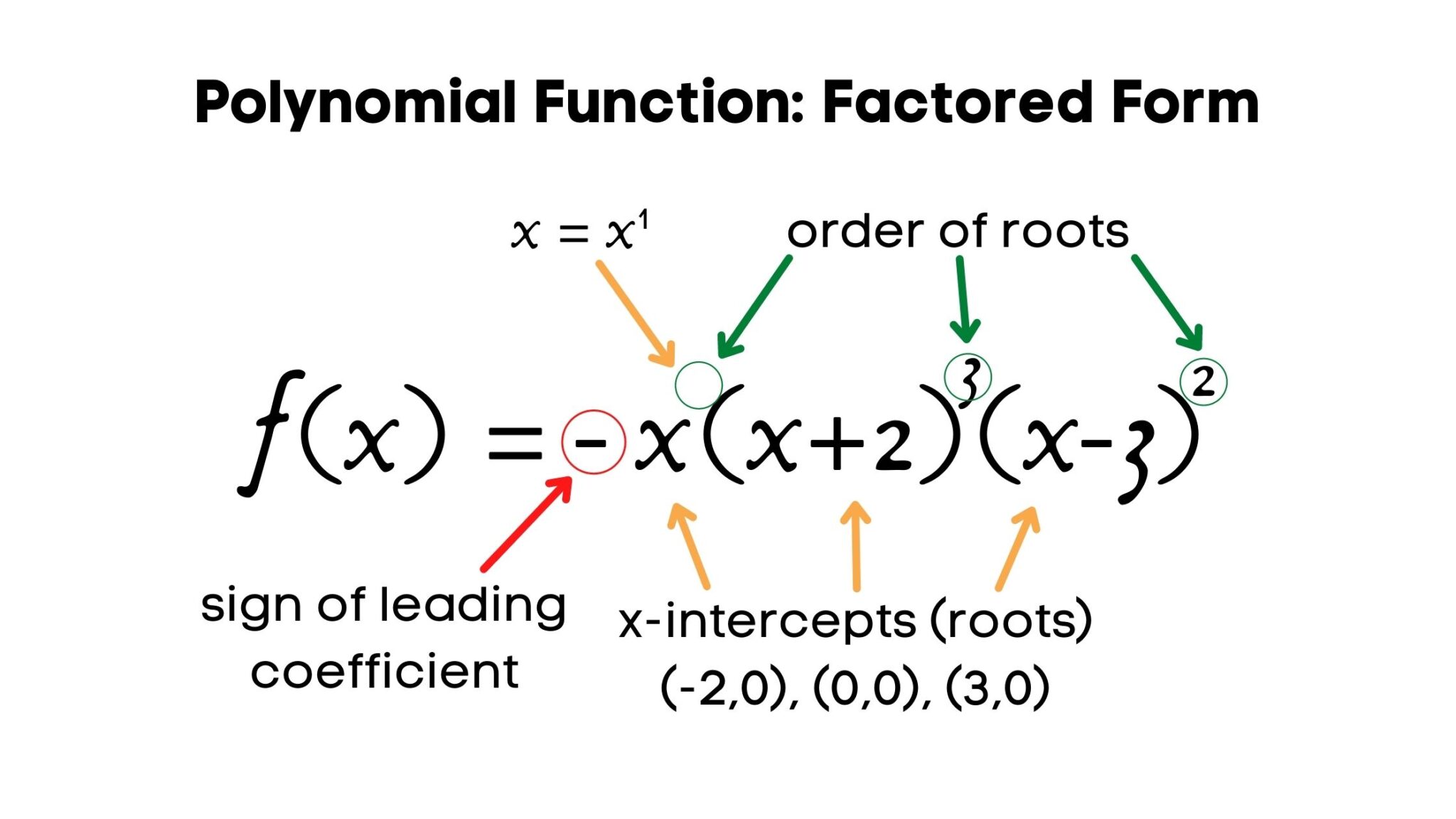
Polynomial Functions Intomath Polynomial functions have all of these characteristics as well as a domain and range, and corresponding graphs. in this section we will identify and evaluate polynomial functions. because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable. The graph of a polynomial will touch and bounce off the x axis at a zero with even multiplicity. the end behavior of a polynomial function depends on the leading term. the graph of a polynomial function changes direction at its turning points. a polynomial function of degree n has at most n – 1 turning points.

Polynomial Functions
Graphs Of Polynomial Functions

Comments are closed.