Chapter 5 3 Part 2 Reference Angles And Evaluating Trig Using Reference

Chapter 5 3 Part 2 Reference Angles And Evaluating Trig Using Reference 150° is located in the second quadrant. the angle it makes with the x axis is 180° − 150° = 30°, so the reference angle is 30°.this tells us that 150° has the same sine and cosine values as 30°, except for the sign. we know that. cos (3 0 ∘) = 3 2 a n d sin (3 0 ∘) = 1 2. Given an angle not in the first quadrant, use reference angles to find all six trigonometric functions. measure the angle formed by the terminal side of the given angle and the horizontal axis. this is the reference angle. evaluate the function at the reference angle. observe the quadrant where the terminal side of the original angle is located.

Evaluating Trig Functions Using Reference Angles Youtube To find the value of a trigonometric function of any angle t: determine the function value for the associated reference angle t'. depending on the quadrant in which t lies, the answer will be either be or . how to evaluate trig functions using reference angles? find the reference angle for the given angle. In this video we look at evaluating trigonometric functions of all angles. we introduce reference angles and use these to help us find trigonometric functio. Example 2. question. evaluate sin 5ˇ 3 and tan 5ˇ 4. answer. the angle 5ˇ 3 is in quadrant iv, so its reference angle is 2ˇ 5ˇ 3 = 6ˇ 3 5ˇ 3 = ˇ 3: sine is negative in quadrant iv, and sin ˇ 3 = p 3 2, so sin 5ˇ 3 = p 3 2. the angle 5ˇ 4 is in quadrant iii, where tangent is positive. its reference angle is 5ˇ 4 ˇ= 5ˇ 4 4ˇ 4 = ˇ. An angle’s reference angle is the measure of the smallest, positive, acute angle t formed by the terminal side of the angle t and the horizontal axis. thus positive reference angles have terminal sides that lie in the first quadrant and can be used as models for angles in other quadrants. see figure 1 for examples of reference angles for.
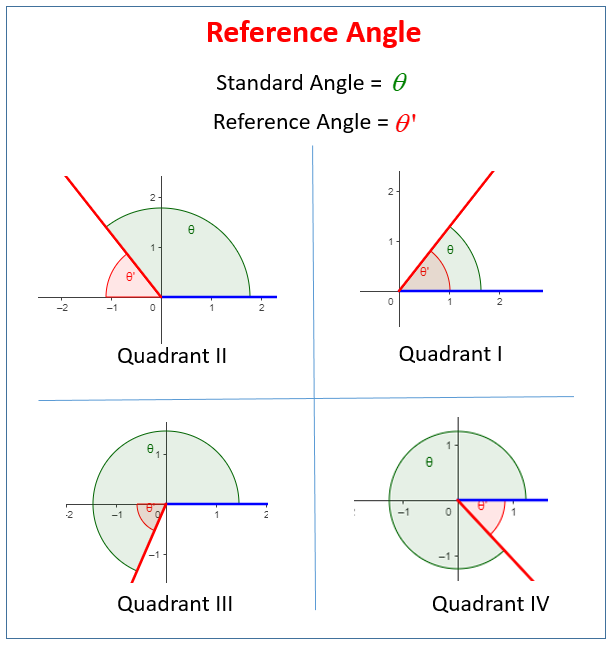
Evaluating Trigonometric Functions Using The Reference Angle Solutions Example 2. question. evaluate sin 5ˇ 3 and tan 5ˇ 4. answer. the angle 5ˇ 3 is in quadrant iv, so its reference angle is 2ˇ 5ˇ 3 = 6ˇ 3 5ˇ 3 = ˇ 3: sine is negative in quadrant iv, and sin ˇ 3 = p 3 2, so sin 5ˇ 3 = p 3 2. the angle 5ˇ 4 is in quadrant iii, where tangent is positive. its reference angle is 5ˇ 4 ˇ= 5ˇ 4 4ˇ 4 = ˇ. An angle’s reference angle is the measure of the smallest, positive, acute angle t formed by the terminal side of the angle t and the horizontal axis. thus positive reference angles have terminal sides that lie in the first quadrant and can be used as models for angles in other quadrants. see figure 1 for examples of reference angles for. Reference angles, by definition, always have a measure between 0 and . due to the periodic nature of the trigonometric functions, the value of a trigonometric function at a given angle is always the same as its value at that angle's reference angle, except when there is a variation in sign. because we know the signs of the functions in. Example 1: find the exact value of sin 135º. (see diagram above) solution: draw the angle in standard position (with initial ray on the x axis and opening counterclockwise). find the reference angle (in this case 45º). draw the reference triangle. label the sides of the triangle with the patterns for a 45º 45º 90º triangle, being careful.

Evaluating Trig Functions With Reference Angles Youtube Reference angles, by definition, always have a measure between 0 and . due to the periodic nature of the trigonometric functions, the value of a trigonometric function at a given angle is always the same as its value at that angle's reference angle, except when there is a variation in sign. because we know the signs of the functions in. Example 1: find the exact value of sin 135º. (see diagram above) solution: draw the angle in standard position (with initial ray on the x axis and opening counterclockwise). find the reference angle (in this case 45º). draw the reference triangle. label the sides of the triangle with the patterns for a 45º 45º 90º triangle, being careful.

Solving Trig Equations Using Reference Angles Youtube
Reference Angle Calculator Trig At Dianne Corriveau Blog

Comments are closed.