Chapter 2 Linear Regression By Ols And Mle Abracadabra Stats

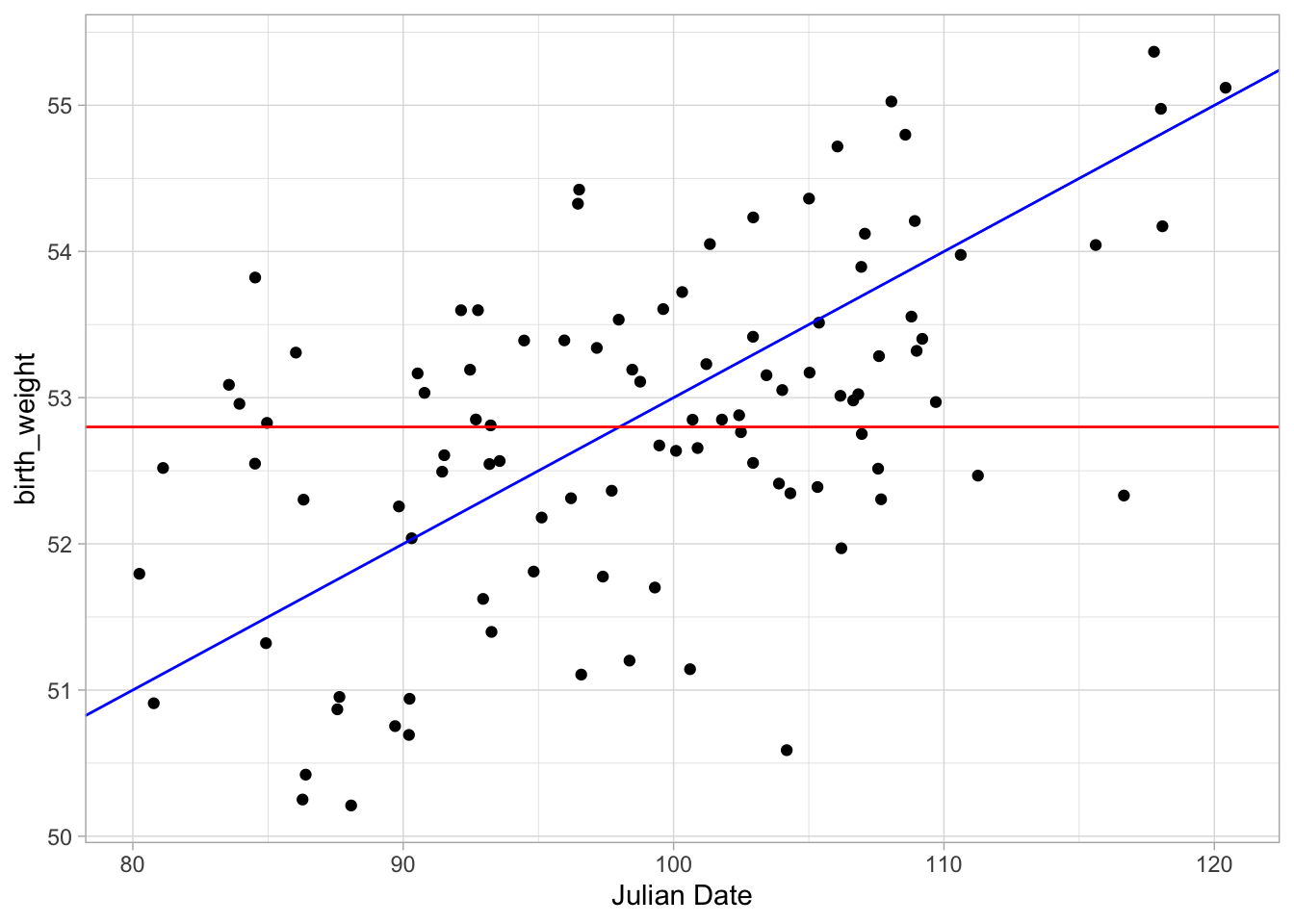
Chapter 2 Linear Regression By Ols And Mle Abracadabra Stats 2.1 ols. in this first chapter we will dive a bit deeper into the methods outlined in the video "what is maximum likelihood estimation (w regression). in the video, we touched on one method of linear regression, least squares regression. recall the general intuition is that we want to minimize the distance each point is from the line. 2 linear regression by ols and mle. 2.1 ols. abracadabra stats companion book. matthew whalen. 2020 10 25. chapter 1 introdction to abracadabra.

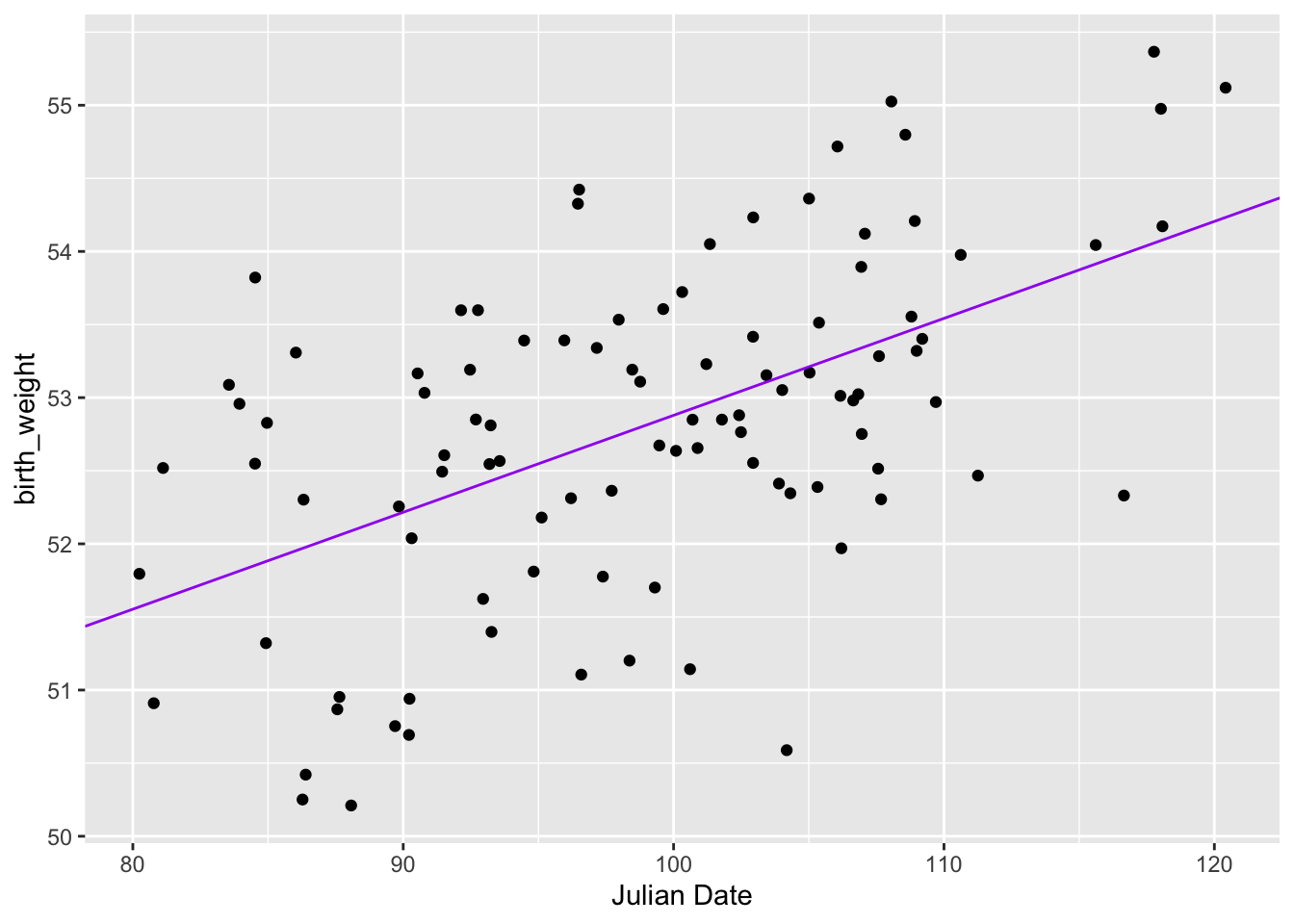
Chapter 2 Linear Regression By Ols And Mle Abracadabra Stats 2 linear regression by ols and mle. 2.1 ols. 2.1.1 the data; 2.1.2 the math; 2.1.3 a tangent on optimizers; 2.2 back to the main stuff; 2.3 multiple parameters; 3 maximum likelihood. 3.0.1 mle for random data; 3.1 mle regression. 3.1.1 another tangent on optimizers; published with bookdown. Here is closely related question, with a derivation of ols in terms of mle. the conditional distribution corresponds to your noise model (for ols: gaussian and the same distribution for all inputs). there are other options (t student to deal with outliers, or allow the noise distribution to depend on the input ). Thus, ols and mle eventually use the same t statistics for regression coefficients. look at this from another angle. we know that ˆσ2 ols = ∑ni = 1 (yi – ˆβ0 − ˆβ1xi)2 n − 2 and ˆσ2 mle = ∑ni = 1 (yi – ˆβ0 − ˆβ1xi)2 n. that is, the difference is in the denominator. however, to construct the v: ˆσ2 ols ∗ (n − 2. Section 1: understanding the ols. ordinary least squares is a method used to estimate the coefficients in a linear regression model by minimizing the sum of the squared residuals.

Mle Vs Ols Maximum Likelihood Vs Least Squares In Linear Regression Thus, ols and mle eventually use the same t statistics for regression coefficients. look at this from another angle. we know that ˆσ2 ols = ∑ni = 1 (yi – ˆβ0 − ˆβ1xi)2 n − 2 and ˆσ2 mle = ∑ni = 1 (yi – ˆβ0 − ˆβ1xi)2 n. that is, the difference is in the denominator. however, to construct the v: ˆσ2 ols ∗ (n − 2. Section 1: understanding the ols. ordinary least squares is a method used to estimate the coefficients in a linear regression model by minimizing the sum of the squared residuals. Theorem 12.1 (ols solution for simple linear regression) for a simple linear regression model with just one predictor for a data set with nn observations, the solution for: arg min β0, β1 n ∑ i = 1(yi − (β0 β1xi))2. is given by: ^ β1 = cov(x, y) var(x) ^ β0 = ˉy − ˆβ1ˉx. show proof. The first entries of the score vector are the th entry of the score vector is the hessian, that is, the matrix of second derivatives, can be written as a block matrix let us compute the blocks: and finally, therefore, the hessian is by the information equality, we have that but and, by the law of iterated expectations, thus, as a consequence, the asymptotic covariance matrix is.

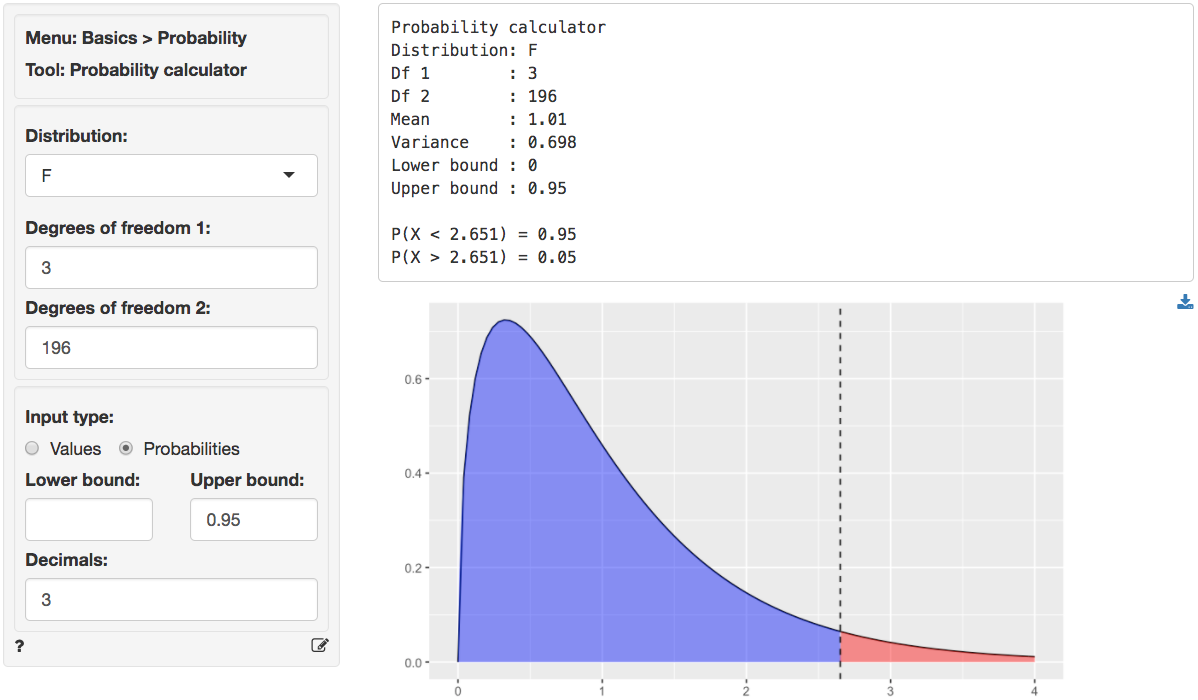
Model Linear Regression Ols Radiant Model Theorem 12.1 (ols solution for simple linear regression) for a simple linear regression model with just one predictor for a data set with nn observations, the solution for: arg min β0, β1 n ∑ i = 1(yi − (β0 β1xi))2. is given by: ^ β1 = cov(x, y) var(x) ^ β0 = ˉy − ˆβ1ˉx. show proof. The first entries of the score vector are the th entry of the score vector is the hessian, that is, the matrix of second derivatives, can be written as a block matrix let us compute the blocks: and finally, therefore, the hessian is by the information equality, we have that but and, by the law of iterated expectations, thus, as a consequence, the asymptotic covariance matrix is.