Chain Rule Practice Problems Solved Derivatives Of Composite

Differentiating Composite Functions Using The Chain Rule Calculus 3.1 the definition of the derivative; 3.2 interpretation of the derivative; 3.3 differentiation formulas; 3.4 product and quotient rule; 3.5 derivatives of trig functions; 3.6 derivatives of exponential and logarithm functions; 3.7 derivatives of inverse trig functions; 3.8 derivatives of hyperbolic functions; 3.9 chain rule; 3.10 implicit. We’ll illustrate in the problems below. chain rule example #1. differentiate . solutions. we’ll solve this using three different approaches — but we encourage you to become comfortable with the third approach as quickly as possible, because that’s the one you’ll use to compute derivatives quickly as the course progresses. • solution 1.

Chain Rule Practice Problems Solved Derivatives Of Composite To find the derivative of composite functions, we will use the chain rule. we can see that the inner function is. 4x^2 1 and the outer function is the sine function. the chain rule states: \large{\frac{d}{dx}f(g(x)) = f'(g(x)) \cdot g'(x)} step 2: applying the chain rule, we have: solution locked! click to view!. To do the chain rule: differentiate the outer function, keeping the inner function the same. multiply this by the derivative of the inner function. for example, differentiate (4𝑥 – 3) 5 using the chain rule. in this example we will use the chain rule step by step. below this, we will use the chain rule formula method. Summary of the chain rule. the chain rule is a very useful tool used to derive a composition of different functions. it is a rule that states that the derivative of a composition of at least two different types of functions is equal to the derivative of the outer function f(u) multiplied by the derivative of the inner function g(x), where u=g(x). Critical thinking question: 13) give a function that requires three applications of the chain rule to differentiate. then differentiate the function. many answers: ex y = ( ( ( 2 x 1)5 2)6 3)7 dy = 7 ( ( ( 2 x 1)5 2)6 3)6 ⋅ 6 ( ( 2 x 1)5 2)5 ⋅ 5 ( 2 x 1)4 ⋅ 2 dx. create your own worksheets like this one with infinite.
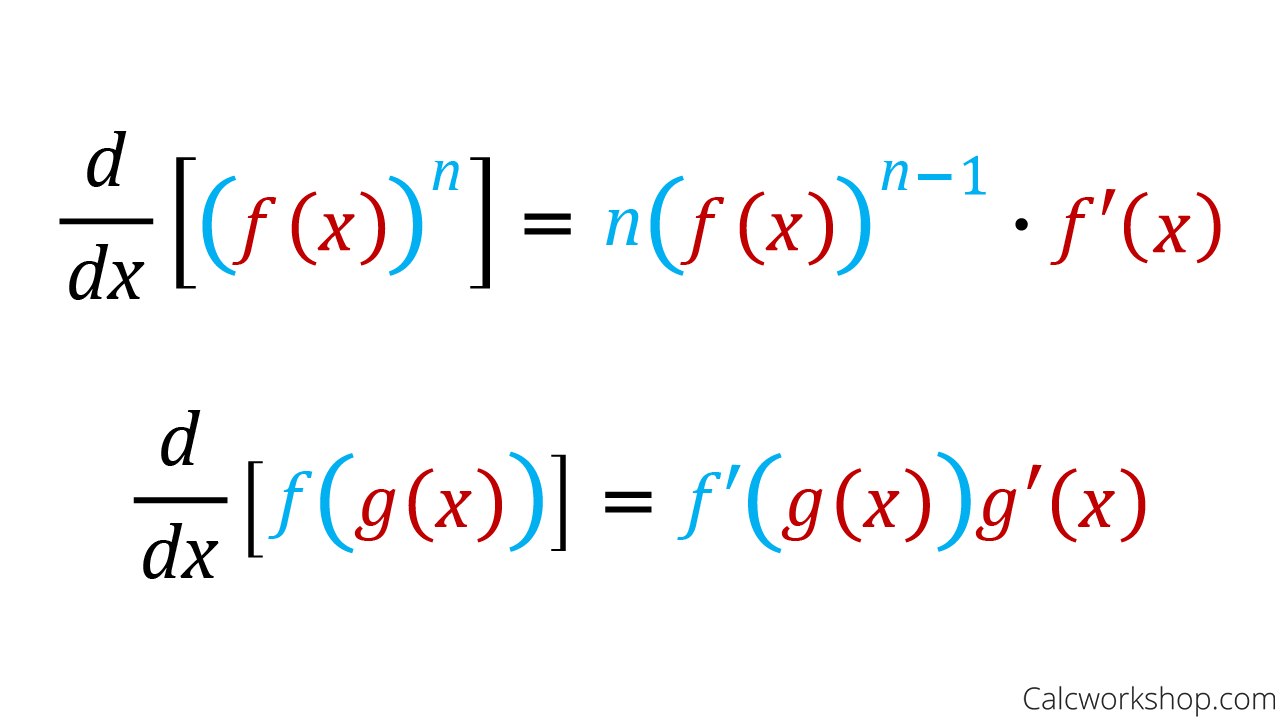
Chain Rule Explained W 7 Step By Step Examples Summary of the chain rule. the chain rule is a very useful tool used to derive a composition of different functions. it is a rule that states that the derivative of a composition of at least two different types of functions is equal to the derivative of the outer function f(u) multiplied by the derivative of the inner function g(x), where u=g(x). Critical thinking question: 13) give a function that requires three applications of the chain rule to differentiate. then differentiate the function. many answers: ex y = ( ( ( 2 x 1)5 2)6 3)7 dy = 7 ( ( ( 2 x 1)5 2)6 3)6 ⋅ 6 ( ( 2 x 1)5 2)5 ⋅ 5 ( 2 x 1)4 ⋅ 2 dx. create your own worksheets like this one with infinite. Worked example. let’s now take a look at a problem to see the chain rule in action as we find the derivative of the following function: chain rule — examples. see, all we did was first take the derivative of the outside function (parentheses), keeping the inside as is. next, we multiplied by the derivative of the inside function, and lastly. %pdf 1.5 %ÐÔÅØ 5 0 obj length 2933 filter flatedecode >> stream xÚí\iwÛÈ ¾ëwðh¾d=½ ‡9Äyždò&«•Óx 4ek|¡d‡¤Ær~}¾Æ&,Ýh@$ ø g@lvw×úuu.

Chain Rule Or Derivative Of Composite Function Worked Examples Worked example. let’s now take a look at a problem to see the chain rule in action as we find the derivative of the following function: chain rule — examples. see, all we did was first take the derivative of the outside function (parentheses), keeping the inside as is. next, we multiplied by the derivative of the inside function, and lastly. %pdf 1.5 %ÐÔÅØ 5 0 obj length 2933 filter flatedecode >> stream xÚí\iwÛÈ ¾ëwðh¾d=½ ‡9Äyždò&«•Óx 4ek|¡d‡¤Ær~}¾Æ&,Ýh@$ ø g@lvw×úuu.
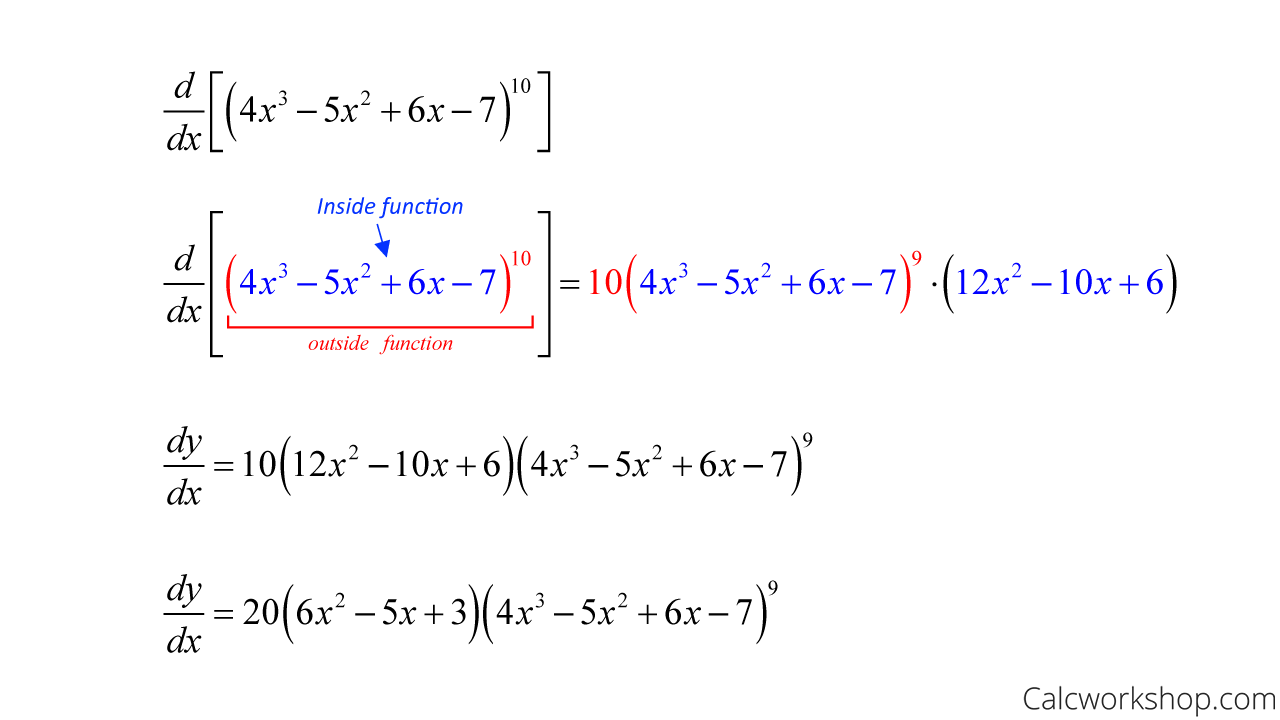
Chain Rule Explained W 7 Step By Step Examples

Comments are closed.