Chain Rule Or Derivative Of Composite Function Worked Examples
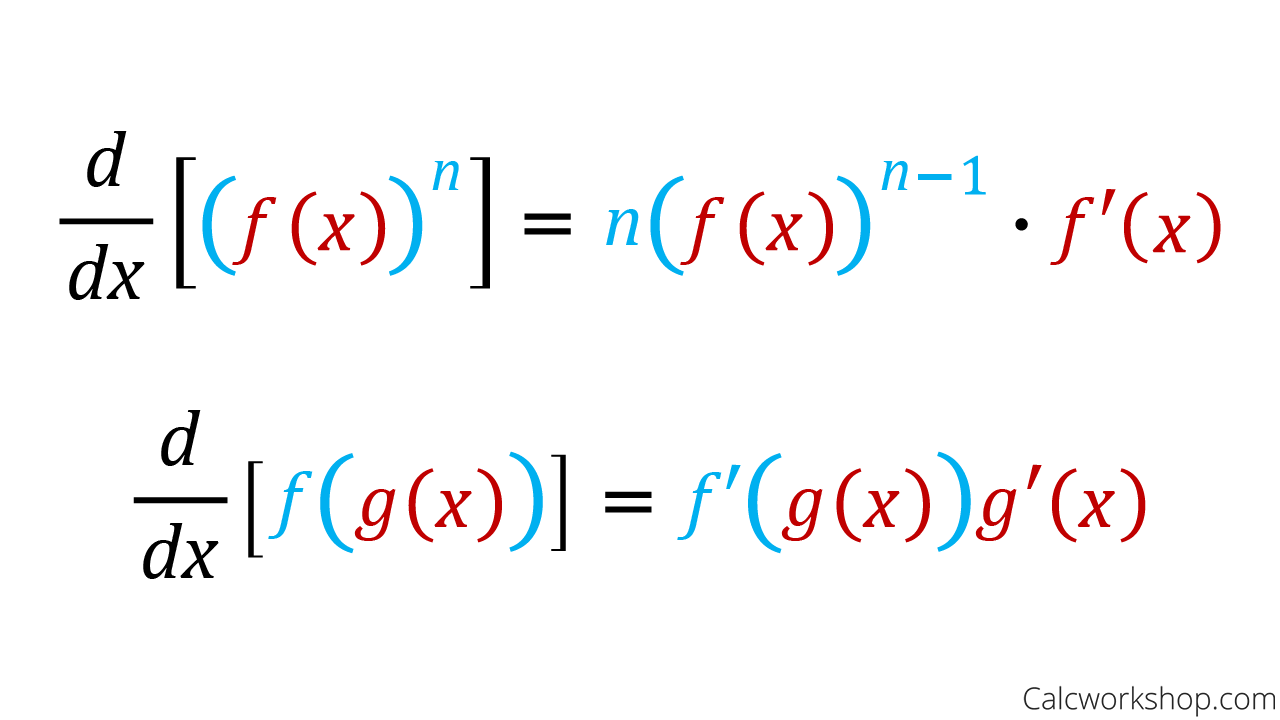
Chain Rule Explained W 7 Step By Step Examples To do the chain rule: differentiate the outer function, keeping the inner function the same. multiply this by the derivative of the inner function. for example, differentiate (4𝑥 – 3) 5 using the chain rule. in this example we will use the chain rule step by step. below this, we will use the chain rule formula method. we define 4𝑥 – 3. Worked example. let’s now take a look at a problem to see the chain rule in action as we find the derivative of the following function: chain rule — examples. see, all we did was first take the derivative of the outside function (parentheses), keeping the inside as is. next, we multiplied by the derivative of the inside function, and lastly.
Differentiating Composite Functions Using The Chain Rule Calculus Derivatives of composite functions in one variable are determined using the simple chain rule formula. let us solve a few examples to understand the calculation of the derivatives: example 1: determine the derivative of the composite function h (x) = (x 3 7) 10. solution: now, let u = x 3 7 = g (x), here h (x) can be written as h (x) = f (g. Note: when applying the chain rule to the composition of two or more functions, keep in mind that we work our way from the outside function in. it is also useful to remember that the derivative of the composition of two functions can be thought of as having two parts; the derivative of the composition of three functions has three parts; and so on. Now let's tackle a worked example of composite functions, using the example f(x) = cos³(x). by applying the chain rule, we differentiate this function, breaking it down into its components x³ and cos(x). this helps us understand how to handle other complex derivatives with ease. Recall that the chain rule for the derivative of a composite of two functions can be written in the form \[\dfrac{d}{dx}\big(f(g(x))\big)=f′\big(g(x)\big)g′(x). \nonumber \] in this equation, both \(f(x)\) and \(g(x)\) are functions of one variable. now suppose that \(f\) is a function of two variables and \(g\) is a function of one variable.

Chain Rule Or Derivative Of Composite Function Worked Examples Now let's tackle a worked example of composite functions, using the example f(x) = cos³(x). by applying the chain rule, we differentiate this function, breaking it down into its components x³ and cos(x). this helps us understand how to handle other complex derivatives with ease. Recall that the chain rule for the derivative of a composite of two functions can be written in the form \[\dfrac{d}{dx}\big(f(g(x))\big)=f′\big(g(x)\big)g′(x). \nonumber \] in this equation, both \(f(x)\) and \(g(x)\) are functions of one variable. now suppose that \(f\) is a function of two variables and \(g\) is a function of one variable. The chain rule. the following figure gives the chain rule that is used to find the derivative of composite functions. scroll down the page for more examples and solutions. in leibniz notation, if y = f(u) and u = g(x) are both differentiable functions, then note: in the chain rule, we work from the outside to the inside. The chain rule is a method for finding the derivative of composite functions, or functions that are made by combining one or more functions. an example of one of these types of functions is \ (f (x) = (1 x)^2\) which is formed by taking the function \ (1 x\) and plugging it into the function \ (x^2\). a surprising number of functions can be.

Derivatives Of Composite Functions The Chain Rule Youtube The chain rule. the following figure gives the chain rule that is used to find the derivative of composite functions. scroll down the page for more examples and solutions. in leibniz notation, if y = f(u) and u = g(x) are both differentiable functions, then note: in the chain rule, we work from the outside to the inside. The chain rule is a method for finding the derivative of composite functions, or functions that are made by combining one or more functions. an example of one of these types of functions is \ (f (x) = (1 x)^2\) which is formed by taking the function \ (1 x\) and plugging it into the function \ (x^2\). a surprising number of functions can be.

рџ 26 Derivative Of Composite Functions The Chain Rule Easyway

Comments are closed.