Case Of Infinite Solutions System Of Equations

Case Of Infinite Solutions System Of Equations Youtube It means that if the system of equations has an infinite number of solution, then the system is said to be consistent. as an example, consider the following two lines. line 1: y = x 3. line 2: 5y = 5x 15. these two lines are exactly the same line. if you multiply line 1 by 5, you get the line 2. The system is said to be inconsistent otherwise, having no solutions. systems of linear equations involving more than two variables work similarly, having either one solution, no solutions or infinite solutions (the latter in the case that all component equations are equivalent).

Simple Ways To Solve Equations With Infinite Solutions A system of equations in 3 variables will have infinite solutions if the planes intersect in an entire line or in an entire plane. the latter case occurs if all three equations are equivalent and represent the same plane. here is an example of the second case: x y z = 1. 2x 2y 2z = 2. 3x 3y 3z = 3. To solve a system of equations by elimination, write the system of equations in standard form: ax by = c, and multiply one or both of the equations by a constant so that the coefficients of one of the variables are opposite. then, add or subtract the two equations to eliminate one of the variables. solve the resulting equation for the. Hence, a system will be consistent if the system of equations has an infinite number of solutions. for example, consider the following equations. y = x 3. 5y = 5x 15. if we multiply 5 to equation 1, we will achieve equation 2 and by dividing equation 2 with 5, we will get the exact first equation. infinite solutions example. A dependent system of equations is a system that has an infinite solution. if the system is two equations in two variables, then the system will graph as one line, because the second equation in the system is actually the same as the first; it will just have been rearranged a bit, and maybe they multiplied through by some number.

Ppt Solving Systems Of Linear Equations Powerpoint Presentation Free Hence, a system will be consistent if the system of equations has an infinite number of solutions. for example, consider the following equations. y = x 3. 5y = 5x 15. if we multiply 5 to equation 1, we will achieve equation 2 and by dividing equation 2 with 5, we will get the exact first equation. infinite solutions example. A dependent system of equations is a system that has an infinite solution. if the system is two equations in two variables, then the system will graph as one line, because the second equation in the system is actually the same as the first; it will just have been rearranged a bit, and maybe they multiplied through by some number. Key idea 1.4.1: consistent solution types. a consistent linear system of equations will have exactly one solution if and only if there is a leading 1 for each variable in the system. if a consistent linear system of equations has a free variable, it has infinite solutions. if a consistent linear system has more variables than leading 1s, then. If any row of the reduced row echelon form of the matrix gives a false statement such as 0 = 1, the system is inconsistent and has no solution. if the reduced row echelon form has fewer equations than the variables and the system is consistent, then the system has an infinite number of solutions. remember the rows that contain all zeros are.

System Of Linear Equations Infinite Solutions Example Youtube Key idea 1.4.1: consistent solution types. a consistent linear system of equations will have exactly one solution if and only if there is a leading 1 for each variable in the system. if a consistent linear system of equations has a free variable, it has infinite solutions. if a consistent linear system has more variables than leading 1s, then. If any row of the reduced row echelon form of the matrix gives a false statement such as 0 = 1, the system is inconsistent and has no solution. if the reduced row echelon form has fewer equations than the variables and the system is consistent, then the system has an infinite number of solutions. remember the rows that contain all zeros are.
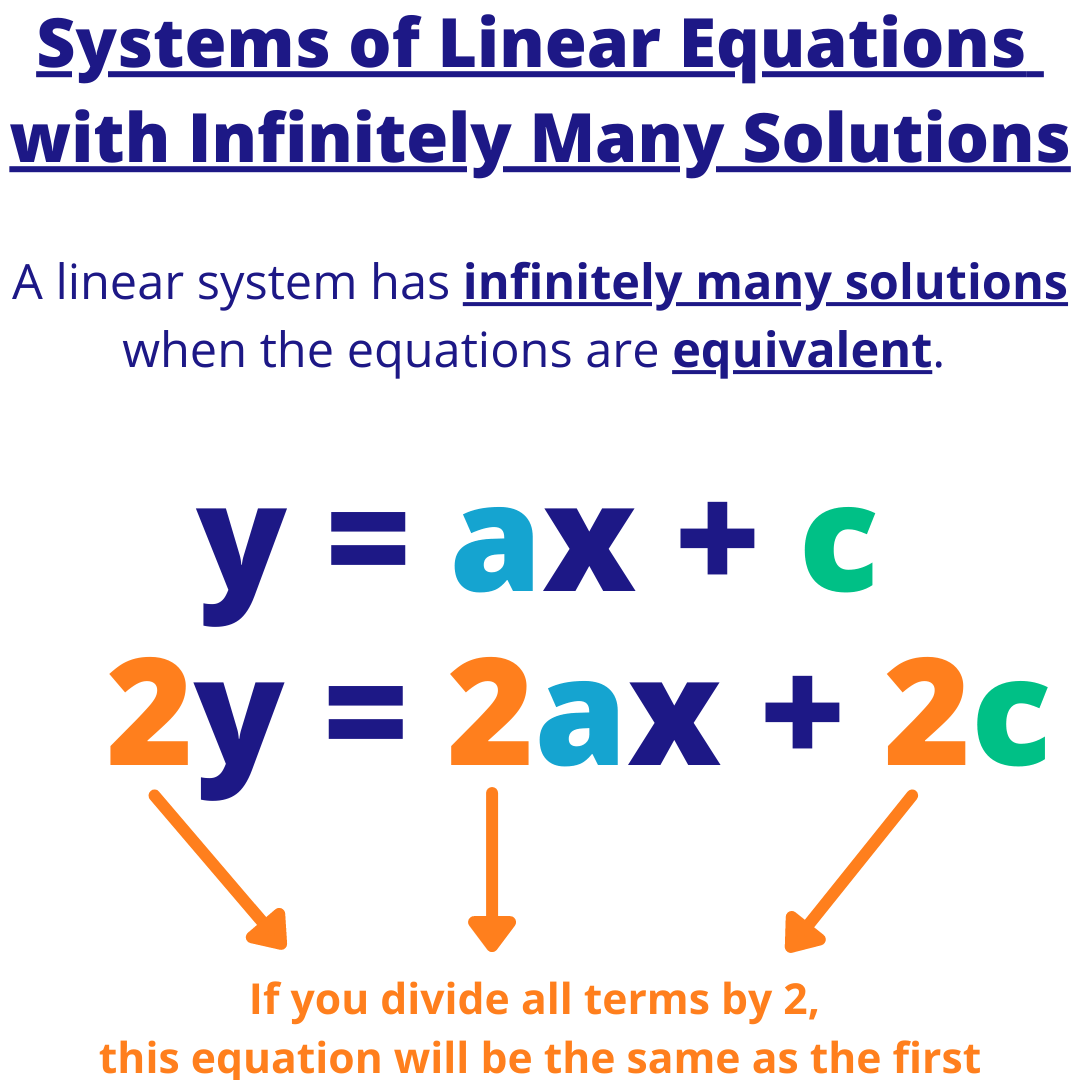
Systems Of Linear Equations With Infinite Solutions Examples Expii

System Of Equations Special Case Infinitely Many Solutions Open Middle

Comments are closed.