Carnot Cycle Heat Pump Actionlasopa

Carnot Cycle Heat Pump Actionlasopa A carnot heat pump (or carnot refrigerator) is a reverse carnot heat engine, that absorbs heat from a cold thermal reservoir and transfers it to a warmer thermal reservoir. as we will show below, it is the most efficient heat pump operating between two given temperatures. first, we will determine the coefficient of performance of the carnot. When a carnot cycle runs in reverse, it is called a reverse carnot cycle. a refrigerator or heat pump that acts according to the reversed carnot cycle is called a carnot refrigerator or carnot heat pump, respectively. in the first stage of this cycle, the refrigerant absorbs heat isothermally from a low temperature source, t l, in the amount q l.
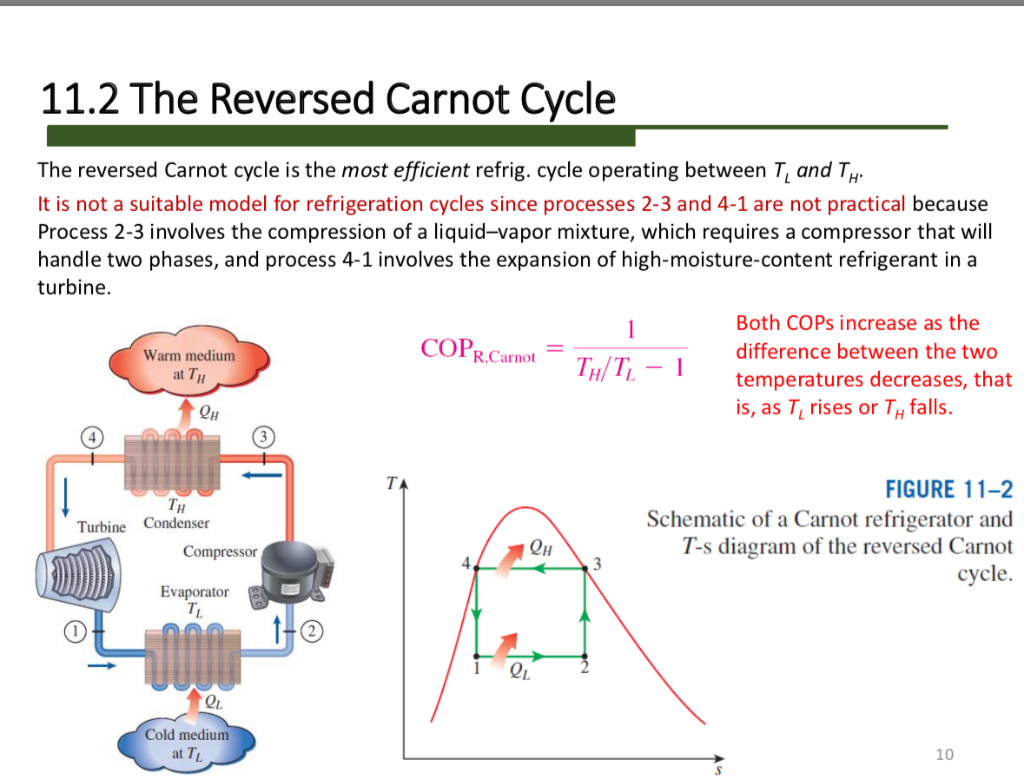
Carnot Cycle Heat Pump Lasopacute The basic components of a heat pump in its heating mode are shown in figure 15.5.3. a working fluid such as a non cfc refrigerant is used. in the outdoor coils (the evaporator), heat transfer qc occurs to the working fluid from the cold outdoor air, turning it into a gas. Heat pumps can't operate at the thermodynamic efficiency limit because you don't want them to take an infinite amount of time to transfer heat into your house. think about a heat engine first. a carnot engine operating "at" thermodynamic efficiency between two reservoirs takes an infinitely long time to complete one cycle. The same schematic may be used to represent a heat pump by replacing the notation “ref” with “hp” in the circular area. figure 6.2.2 schematic of a refrigerator (or a heat pump) applying the first law of thermodynamics to the cycle, we can write. q˙h −q˙l = w˙in (6.3.1) (6.3.1) q ˙ h − q ˙ l = w ˙ i n. the main purpose of. Copcoefficient of performance of carnot (reversible) refrigerators and heat pumps. like and subscribe! and get the notes here:thermodynamics: drive.g.

Carnot Cycle Heat Pump Grlasopa The same schematic may be used to represent a heat pump by replacing the notation “ref” with “hp” in the circular area. figure 6.2.2 schematic of a refrigerator (or a heat pump) applying the first law of thermodynamics to the cycle, we can write. q˙h −q˙l = w˙in (6.3.1) (6.3.1) q ˙ h − q ˙ l = w ˙ i n. the main purpose of. Copcoefficient of performance of carnot (reversible) refrigerators and heat pumps. like and subscribe! and get the notes here:thermodynamics: drive.g. Either a refrigerator or a heat pump is an engine running in reverse. for a refrigerator, the focus is on removing heat from a specific area. for a heat pump, the focus is on dumping heat to a specific area. we first consider a refrigerator (figure 4.4.1 4.4. 1). the purpose of this engine is to remove heat from the cold reservoir, which is the. Heat pump. a heat pump is a device which applies external work to extract an amount of heat q c from a cold reservoir and delivers heat q h to a hot reservoir. a heat pump is subject to the same limitations from the second law of thermodynamics as any other heat engine and therefore a maximum efficiency can be calculated from the carnot cycle.

A Carnot Heat Pump Cycle Operating At Steady State With Ammonia As The Either a refrigerator or a heat pump is an engine running in reverse. for a refrigerator, the focus is on removing heat from a specific area. for a heat pump, the focus is on dumping heat to a specific area. we first consider a refrigerator (figure 4.4.1 4.4. 1). the purpose of this engine is to remove heat from the cold reservoir, which is the. Heat pump. a heat pump is a device which applies external work to extract an amount of heat q c from a cold reservoir and delivers heat q h to a hot reservoir. a heat pump is subject to the same limitations from the second law of thermodynamics as any other heat engine and therefore a maximum efficiency can be calculated from the carnot cycle.

Comments are closed.