Calculus Differentiation Derivative Of Sin X From First Principle

Calculus Differentiation Derivative Of Sin X From First Principle The derivative of \\sin(x) can be found from first principles. doing this requires using the angle sum formula for sin, as well as trigonometric limits. In this article, we will prove the derivative of sinus, or in other words, the derivative of \sin (x) sin(x), using first principle of derivatives. we know that the derivative of \sin (x) sin(x) is \cos (x) cos(x), but we would also like to see how to prove that by the definition of the derivative. proof. let f (x) = \sin (x) f (x) = sin(x). then.

Derivative Of Sin X From First Principles Youtube Calculus fundamentals. understand the mathematics of continuous change. derivative by first principle refers to using algebra to find a general expression for the slope of a curve. it is also known as the delta method. the derivative is a measure of the instantaneous rate of change, which is equal to. \ [ f' (x) = \lim {h \rightarrow 0 } \frac. Differentiating sin (x) from first principles. when delving into calculus, particularly in the study of differentiation, a fundamental concept arises: differentiating sine functions using first principles. this method, foundational in calculus, involves determining the derivative of the sine function by applying the limit definition of the. To prove derivative of sin x using first principle of derivative, we will use basic limits and trigonometric formulas which are listed below: sin (x y) = sin x cos y sin y cos x. lim x→0 [sin x x] = 1. lim x→0 [ (cos x – 1) x] = 0. let’s start the proof for the derivative of sin x. by the first principle of derivative. The derivative of sin x with respect to x is cos x. it is mathematically written as d dx(sin x) (or) (sin x)' = cos x. learn the derivative of sin x formula along with its proof using the first principle and graphical intuition.

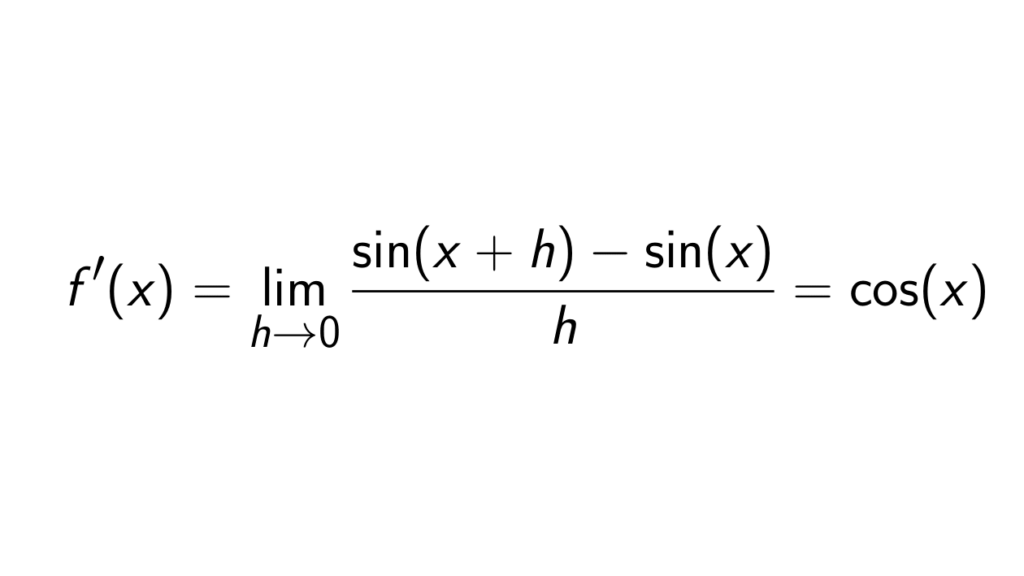
Derivative Of Sin X Using First Principle Of Derivatives Epsilonify To prove derivative of sin x using first principle of derivative, we will use basic limits and trigonometric formulas which are listed below: sin (x y) = sin x cos y sin y cos x. lim x→0 [sin x x] = 1. lim x→0 [ (cos x – 1) x] = 0. let’s start the proof for the derivative of sin x. by the first principle of derivative. The derivative of sin x with respect to x is cos x. it is mathematically written as d dx(sin x) (or) (sin x)' = cos x. learn the derivative of sin x formula along with its proof using the first principle and graphical intuition. Now, let us discuss the first principle method to find the derivative of sin x. derivative of sin x using the first principle method. the derivative of any function can be found using the limit definition of the derivative. (i.e) first principle. so, now we are going to apply the first principle method to find the derivative of sin x as well. To do differentiation by first principles: find f (x h) by substituting x with x h in the f (x) equation. substitute f (x h) and f (x) into the first principles equation. simplify the numerator. divide all terms by h. substituting h=0 to evaluate the limit.

Derivative Of Sin X By Method Of First Principle Youtube Now, let us discuss the first principle method to find the derivative of sin x. derivative of sin x using the first principle method. the derivative of any function can be found using the limit definition of the derivative. (i.e) first principle. so, now we are going to apply the first principle method to find the derivative of sin x as well. To do differentiation by first principles: find f (x h) by substituting x with x h in the f (x) equation. substitute f (x h) and f (x) into the first principles equation. simplify the numerator. divide all terms by h. substituting h=0 to evaluate the limit.