Calculus 2 Integration Trig Substitution 1 Of 28 What Is When To

Calculus 2 Integration Trig Substitution 1 Of 28 What Is When To Visit ilectureonline for more math and science lectures!in this video i will explain what is and how and when to use trig substitution for integra. Here is a summary for the sine trig substitution. √a2 − b2x2 ⇒ x = a bsinθ, − π 2 ≤ θ ≤ π 2. there is one final case that we need to look at. the next integral will also contain something that we need to make sure we can deal with. example 5 evaluate the following integral. ∫ 1 60 x5 (36x2 1)3 2 dx. show solution.

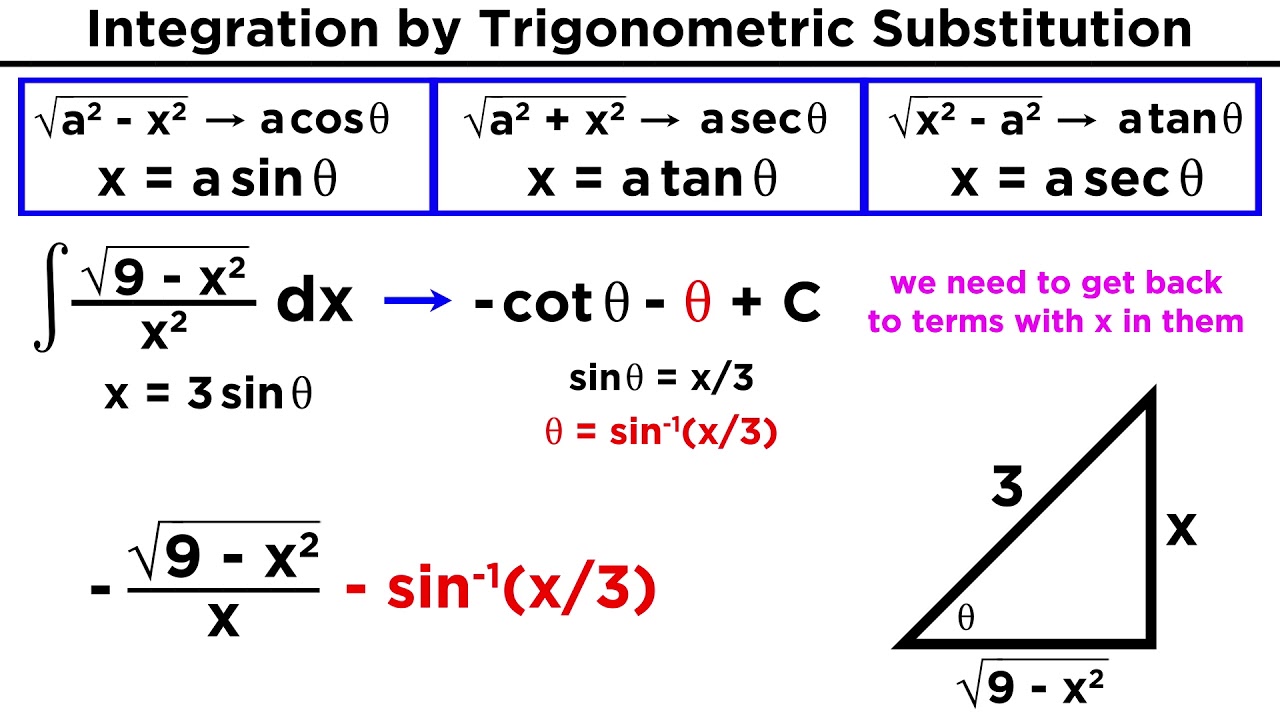
Integration By Trigonometric Substitution Youtube In fact to eliminate the remaining problem term all that we need to do is reuse the first half angle formula given above. so, this solution required a total of three trig identities to complete. solution 2. in this solution we will use the double angle formula to help simplify the integral as follows. Recognizing the integrand as an even power of cosine, we refer to our handout on trig integrals and nd the identity cos2 x= (1 cos(2x))=2. therefore: p 2 4 z cos2 d = p 2 4 z 1 cos(2 ) 2 d = p 2 8 z (1 cos(2 )) d = p 2 8 1 2 sin(2 ) c:: note that the integral of cos(2 ) with respect to requires u substitution with u= 2 . The strategy is to use a trigonometric identity to rewrite the integrand in an alternative form which does not include powers of sin x. the trigonometric identity we shall use here is one of the ‘double angle’ formulae: cos 2a = 1 − 2 sin2 a. by rearranging this we can write. sin2 a =. (1 − cos 2a). To convert back to x x, use your substitution to get x a = tan θ x a = tan. ⁡. θ, and draw a right triangle with opposite side x x, adjacent side a a and hypotenuse x2 a2− −−−−−√ x 2 a 2. when a2 −x2 a 2 − x 2 is embedded in the integrand, use x = a sin(θ) x = a sin. ⁡. (θ).

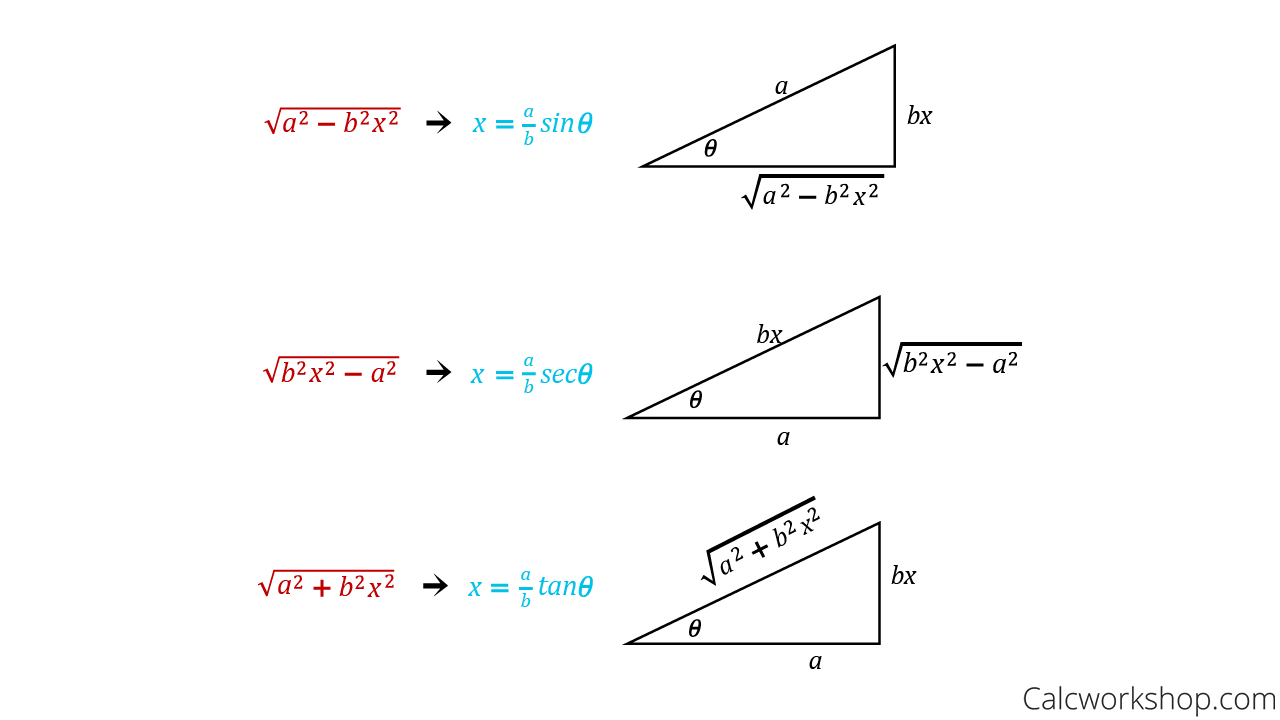
Trig Substitution Your New Best Friend In Calculus The strategy is to use a trigonometric identity to rewrite the integrand in an alternative form which does not include powers of sin x. the trigonometric identity we shall use here is one of the ‘double angle’ formulae: cos 2a = 1 − 2 sin2 a. by rearranging this we can write. sin2 a =. (1 − cos 2a). To convert back to x x, use your substitution to get x a = tan θ x a = tan. ⁡. θ, and draw a right triangle with opposite side x x, adjacent side a a and hypotenuse x2 a2− −−−−−√ x 2 a 2. when a2 −x2 a 2 − x 2 is embedded in the integrand, use x = a sin(θ) x = a sin. ⁡. (θ). This integral cannot be evaluated using any of the techniques we have discussed so far. however, if we make the substitution x = 3sinθ, we have dx = 3cosθdθ. after substituting into the integral, we have ∫√9 − x2dx = ∫√9 − (3sinθ)2 ⋅ 3cosθdθ. after simplifying, we have ∫√9 − x2dx = ∫9√1 − sin2θ ⋅ cosθdθ. Calculus 2 6 units · 105 skills. unit 1 integrals review. unit 2 integration techniques. unit 3 differential equations. unit 4 applications of integrals. unit 5 parametric equations, polar coordinates, and vector valued functions. unit 6 series. course challenge. test your knowledge of the skills in this course.

Calculus Ii Trig Substitution Integral Youtube This integral cannot be evaluated using any of the techniques we have discussed so far. however, if we make the substitution x = 3sinθ, we have dx = 3cosθdθ. after substituting into the integral, we have ∫√9 − x2dx = ∫√9 − (3sinθ)2 ⋅ 3cosθdθ. after simplifying, we have ∫√9 − x2dx = ∫9√1 − sin2θ ⋅ cosθdθ. Calculus 2 6 units · 105 skills. unit 1 integrals review. unit 2 integration techniques. unit 3 differential equations. unit 4 applications of integrals. unit 5 parametric equations, polar coordinates, and vector valued functions. unit 6 series. course challenge. test your knowledge of the skills in this course.

Calculus 2 Integration Trig Substitution 2 Of 28 Applicable