Calculating Mean Deviation For Grouped Data By Peeyush Malhotra

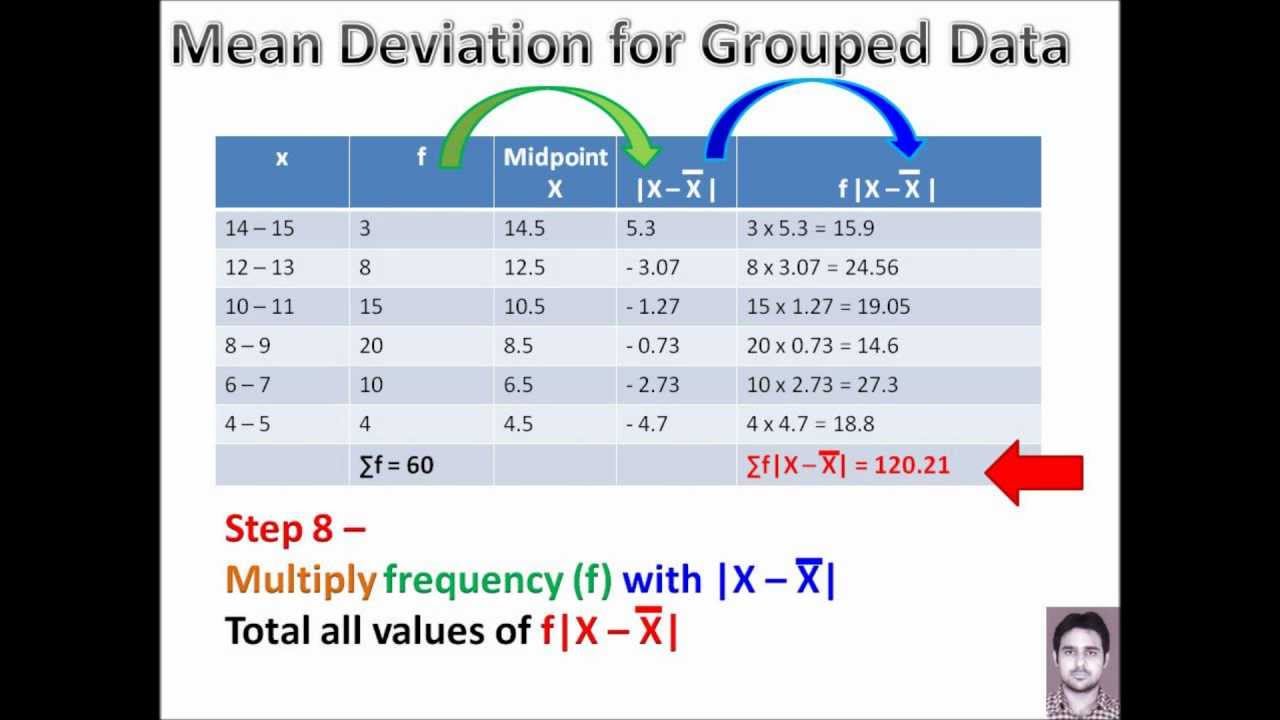
Calculating Mean Deviation For Grouped Data By Peeyush Malhotra This video will teach you how to calculate 'mean deviation' for a grouped data explained by peeyush malhotra gurdaspuria. Methods of calculating 'mean deviation' when the data is grouped and when it is ungrouped. explained by peeyush malhotra gurdaspuria.

Calculating Standard Deviation For Grouped Data Explained By Peeyush Calculate the standard deviation of grouped data. we can use the following formula to estimate the standard deviation of grouped data: standard deviation: √Σni(mi μ)2 (n 1) where: ni: the frequency of the ith group. mi: the midpoint of the ith group. μ: the mean. n: the total sample size. here’s how we would apply this formula to our. 97. we’ll need this both for the mean and for the standard deviation. step 2: find the midpoint of each interval range. to find the midpoint, add the top and bottom of each interval range and divide by two. for example, the first interval range is 37 to 46, so the midpoint is: (37 46) 2 = 83 2 = 41.5. There are two different formulas for calculating the mean for ungrouped data and the mean for grouped data. let us look at the formula to calculate the mean of grouped data. the formula is: x̄ = Σf i i n. where, x̄ = the mean value of the set of given data. f = frequency of the individual data. n = sum of frequencies. Mean deviation of grouped data. in frequency distribution of continuous type, the class intervals or groups are arranged so that there are no gaps between the classes and each class in the table has its respective frequency. the class intervals are chosen in such a way that they must be mutually exclusive and exhaustive.

Step Deviation Method For Calculating Mean In A Class By Peeyush There are two different formulas for calculating the mean for ungrouped data and the mean for grouped data. let us look at the formula to calculate the mean of grouped data. the formula is: x̄ = Σf i i n. where, x̄ = the mean value of the set of given data. f = frequency of the individual data. n = sum of frequencies. Mean deviation of grouped data. in frequency distribution of continuous type, the class intervals or groups are arranged so that there are no gaps between the classes and each class in the table has its respective frequency. the class intervals are chosen in such a way that they must be mutually exclusive and exhaustive. Median and interquartilerange – grouped data. step 1: construct the cumulative frequency distribution. step 2: decide the class that contain the median. class median is the first class with the value of cumulative frequency equal at least n 2. step 3: find the median by using the following formula: ⎛ n ⎞ ⎜ f ⎟. Calculate the standard deviation of grouped data. we can use the following formula to estimate the standard deviation of grouped data: standard deviation: √ Σn i (m i μ) 2 (n 1) where: n i: the frequency of the i th group; m i: the midpoint of the i th group; μ: the mean; n: the total sample size; here’s how we would apply this formula.

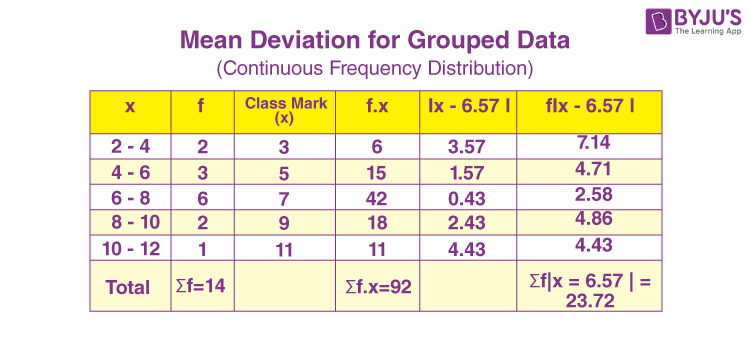
Mean Deviation For Grouped Data Continuous Frequency Distribution Median and interquartilerange – grouped data. step 1: construct the cumulative frequency distribution. step 2: decide the class that contain the median. class median is the first class with the value of cumulative frequency equal at least n 2. step 3: find the median by using the following formula: ⎛ n ⎞ ⎜ f ⎟. Calculate the standard deviation of grouped data. we can use the following formula to estimate the standard deviation of grouped data: standard deviation: √ Σn i (m i μ) 2 (n 1) where: n i: the frequency of the i th group; m i: the midpoint of the i th group; μ: the mean; n: the total sample size; here’s how we would apply this formula.

3 Example2 Calculating Mean And Standard Deviation For Grouped Data

Shortcut Method Of Calculating Mean By Peeyush Malhotra Gurdaspuria Wmv