Calculate Area Of Any Polygon In Coordinate Geometry

Calculate Area Of Any Polygon In Coordinate Geometry Youtube Area of a polygon. (coordinate geometry) a method for finding the area of any polygon when the coordinates of its vertices are known. (see also: computer algorithm for finding the area of any polygon.) first, number the vertices in order, going either clockwise or counter clockwise, starting at any vertex. the area is then given by the formula. (. Polygon area calculator. the calculator below will find the area of any polygon if you know the coordinates of each vertex. this will work for triangles, regular and irregular polygons, convex or concave polygons. it uses the same method as in area of a polygon but does the arithmetic for you. x.

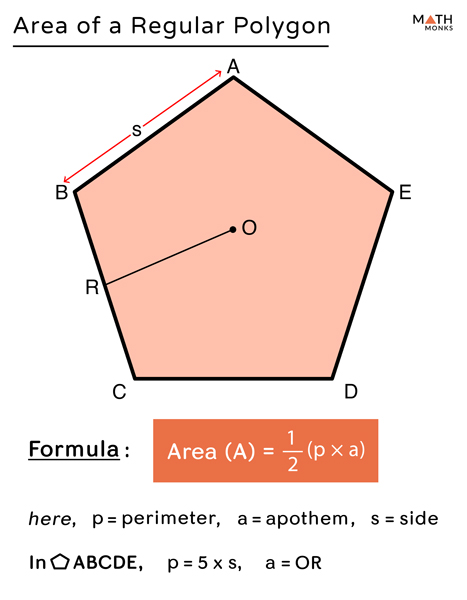
Area Of Polygon Formulas Examples This video illustrates a really efficient method to calculate the area of any polygon whose coordinates are specified.speed maths videos:divisibility rules(a. We’ll look at one more way to find area, using coordinates of vertices, before concluding with the most practical application of all these ideas: finding the area of a plot of land. area of a polygon from coordinates. there are several ways to express the formula we’re interested in; i’ll introduce a couple of them, and then show a proof. Find the area of a regular polygon with perimeter of 44 cm and apothem length of 10 cm. solution: as we know, area (a) = ½ x p x a, here p = 44 cm and a = 10 cm. = ½ x 44 x 10 cm 2. = 220 cm 2. finding the area of regular polygon when the side and apothem are known. calculate the area of a regular pentagon with side 12 cm and apothem of 7.5 cm. A polygon is an area enclosed by multiple straight lines, with a minimum of three straight lines, called a triangle, to a limitless maximum of straight lines. calculating the perimeter and area of a polygon is an often discussed topic in geometry and is the essence and soul of geometry, with the exception of circles or curved lines.

How To Find The Area Of Regular Polygons With Examples Find the area of a regular polygon with perimeter of 44 cm and apothem length of 10 cm. solution: as we know, area (a) = ½ x p x a, here p = 44 cm and a = 10 cm. = ½ x 44 x 10 cm 2. = 220 cm 2. finding the area of regular polygon when the side and apothem are known. calculate the area of a regular pentagon with side 12 cm and apothem of 7.5 cm. A polygon is an area enclosed by multiple straight lines, with a minimum of three straight lines, called a triangle, to a limitless maximum of straight lines. calculating the perimeter and area of a polygon is an often discussed topic in geometry and is the essence and soul of geometry, with the exception of circles or curved lines. If you also wonder how to use coordinates to find the perimeter of polygons, i wrote a whole article that i encourage you to read. step 1: plot the points. step 2: connect the points. step 3: divide into triangles. step 4: find the base and height. step 5: calculate the area of each triangle. step 6: sum up the areas. Going down one side of the polygon adds all the grey area shown here. then going up the other side of the polygon subtracts all the yellow area shown here, because when a side is going up, y0 y1 is a negative number. the area that wasn't subtracted (grey) is the area of the polygon. you don't have to start at the top of the polygon.

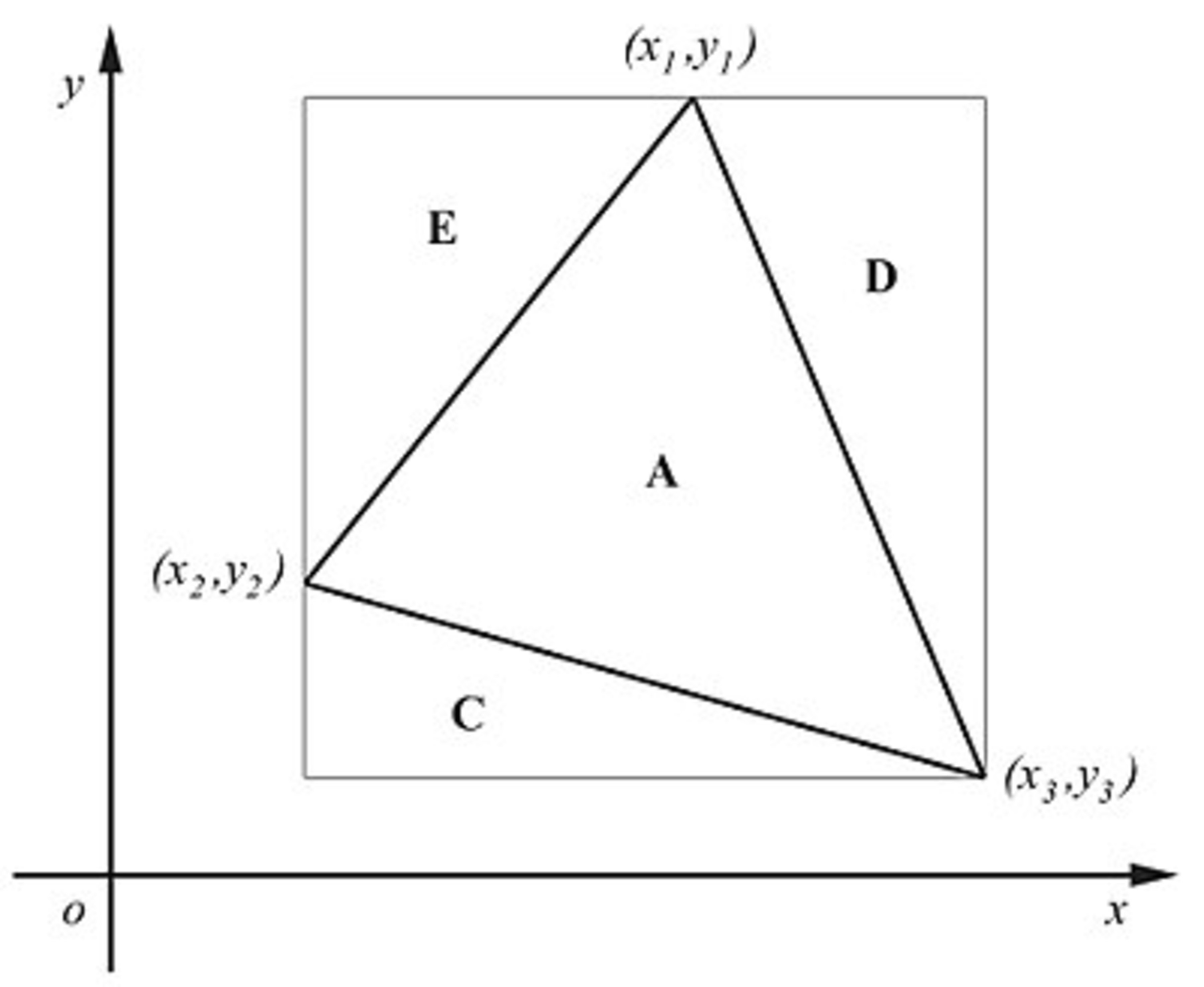
Area Of A Polygon Brilliant Math Science Wiki If you also wonder how to use coordinates to find the perimeter of polygons, i wrote a whole article that i encourage you to read. step 1: plot the points. step 2: connect the points. step 3: divide into triangles. step 4: find the base and height. step 5: calculate the area of each triangle. step 6: sum up the areas. Going down one side of the polygon adds all the grey area shown here. then going up the other side of the polygon subtracts all the yellow area shown here, because when a side is going up, y0 y1 is a negative number. the area that wasn't subtracted (grey) is the area of the polygon. you don't have to start at the top of the polygon.