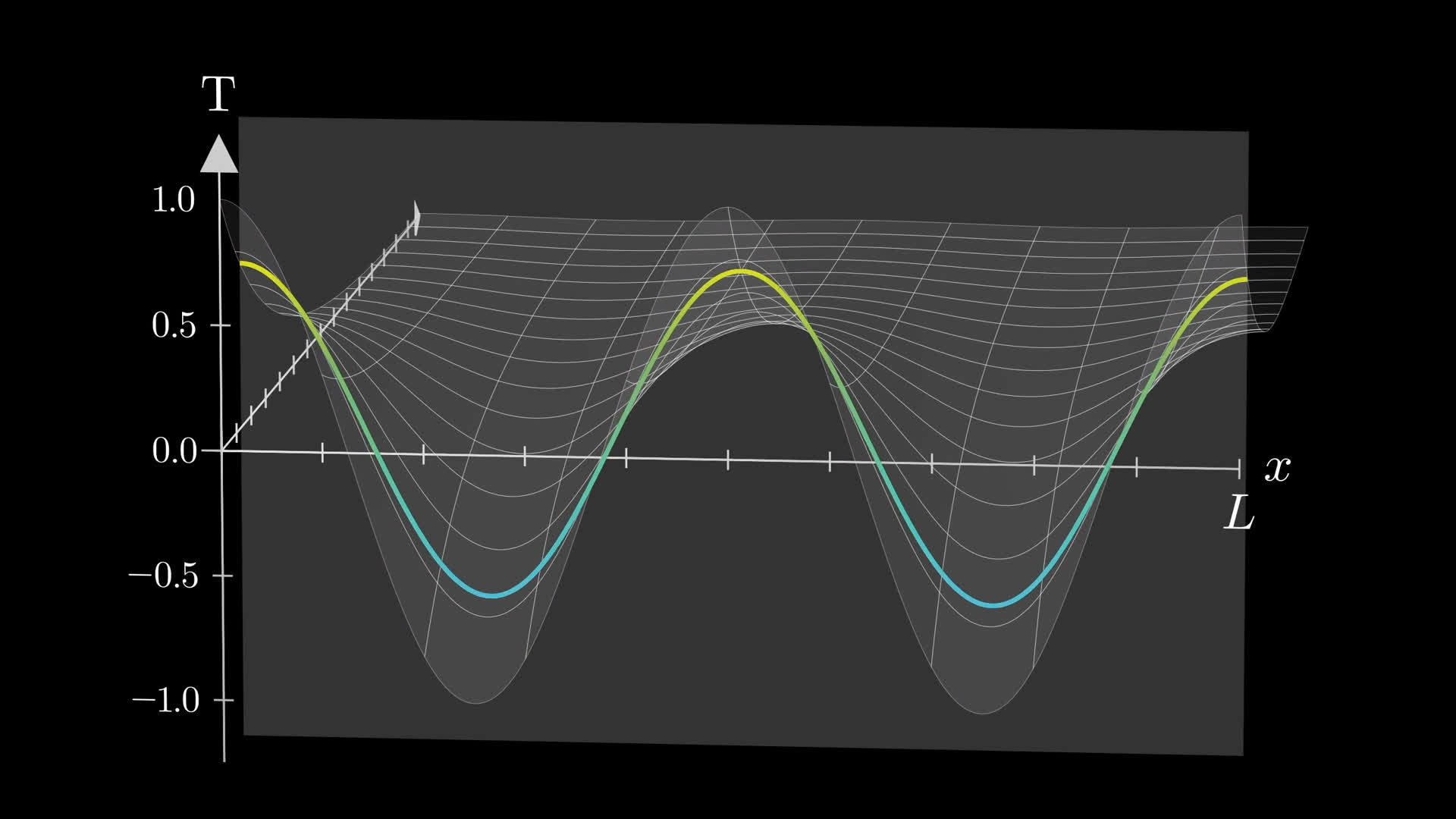
3blue1brown But What Is A Fourier Series From Heat Flow To Circle Fourier series, from the heat equation epicycles.help fund future projects: patreon 3blue1brownan equally valuable form of support is to simp. What i’m describing, finer and finer sums of f (t) for a sample of t from the input range, is an integral of f (t) from 0 to 1. c 0 = \int {0}^ {1} f (t) dt c0 = ∫ 01 f (t)dt. normally, since the aim is to compute an average, you’d divide this integral by the length of the interval. but that length is 1, so it amounts to the same thing.
But What Is A Fourier Series From Heat Flow To Drawing With Circles It's too bad that the people behind the svg specification didn't think of using these fourier coefficients as a way of compressing the data used to draw a looping path. instead of using spline and bezier values, just store a list of fourier coefficients, starting with c (0), then c (1), then c ( 1), and so on until you have specified enough. But what is a fourier series? from heat flow to circle drawings | de4. published jun 30, 2019. lesson by grant sanderson. differential equations. differential equations, studying the unsolvable | de1 but what is a partial differential equation? | de2 solving the heat equation | de3 e^ (iπ) in 3.14 minutes, using dynamics | de5 how (and why) to. Explore the fascinating world of fourier series in this 25 minute video that takes you from heat flow equations to drawing with circles. delve into the mathematical concepts behind infinite function sums, trigonometry in the complex plane, and complex exponential summation. The direction of rotation is determined by the order of the data points. thus, when you do the fourier transform, each term is associated with a particular frequency, some of which are positive and some of which are negative. the positive frequencies rotate counterclockwise by convention and the negative frequencies rotate in the opposite.
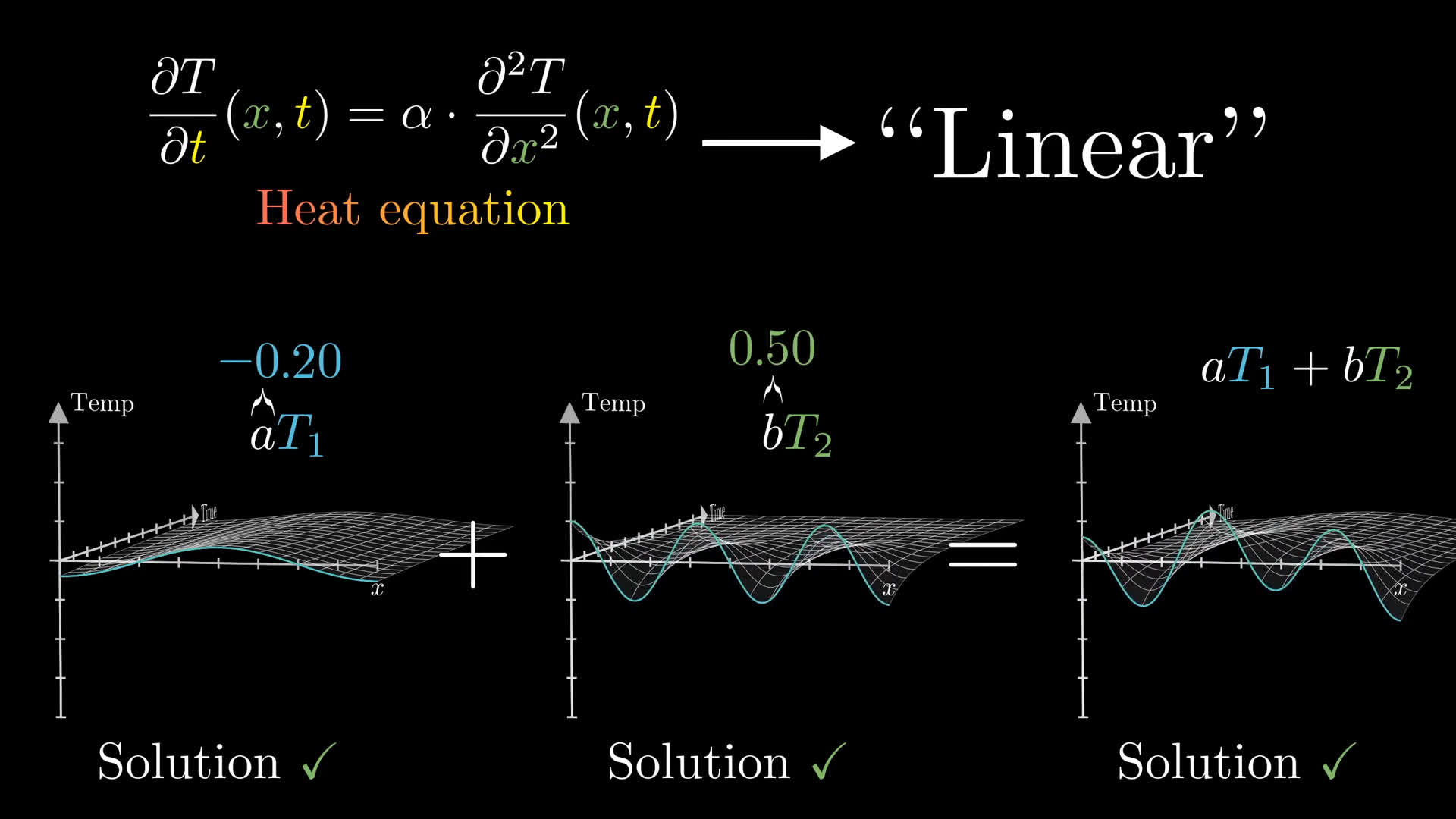
3blue1brown But What Is A Fourier Series From Heat Flow To Circle Explore the fascinating world of fourier series in this 25 minute video that takes you from heat flow equations to drawing with circles. delve into the mathematical concepts behind infinite function sums, trigonometry in the complex plane, and complex exponential summation. The direction of rotation is determined by the order of the data points. thus, when you do the fourier transform, each term is associated with a particular frequency, some of which are positive and some of which are negative. the positive frequencies rotate counterclockwise by convention and the negative frequencies rotate in the opposite. The main idea of the fourier series was to solve all the simple induvidual terms and by sumation end up at the complete function given enough terms. the generel form of fourier series is defined by the expression bellow. f(x) = a0 2 ∑k=1∞ akcos2πkx t ∑k=1∞ bksin2πkx t, f (x) = a 0 2 ∑ k = 1 ∞ a k c o s 2 π k x t ∑ k = 1. From heat flow to circle drawings | de4 fourier series, from the heat equation to sines to cycles. some viewers made apps that create circle animations for.
Comments are closed.