Basic Functions Review Part One

Basic Functions Review Part One Youtube These types of functions are known as piecewise defined functions. for example, suppose we want to define a function f with a domain that is the set of all real numbers such that f(x) = 3x 1 for x ≥ 2 and f(x) = x2 for x <2. we denote this function by writing. f(x) = {3x 1 x ≥ 2 x2 x <2. when evaluating this function for an input x, the. A function is a special type of relation in which each element of the first set is related to exactly one element of the second set. the element of the first set is called the input; the element of the second set is called the output. functions are used all the time in mathematics to describe relationships between two sets.

Review Of Function Part 1 Youtube Neither. logistic function. y= 1 (1 e^ x) neither. bounded above and below. tangent. y= tan x. study with quizlet and memorize flashcards containing terms like identity function y=x odd, squaring function y=x^2 even bounded below, cubing function y=x^3 odd and more. Chapter 1 numbers and functions the subject of this course is \functions of one real variable" so we begin by wondering what a real number \really" is, and then, in the next section, what a function is. 1. what is a number? 1.1. di erent kinds of numbers. the simplest numbers are the positive integers 1;2;3;4; the number zero 0; and the. Make new functions from two or more given functions. describe the symmetry properties of a function. in this section, we provide a formal definition of a function and examine several ways in which functions are represented—namely, through tables, formulas, and graphs. we study formal notation and terms related to functions. All throughout a calculus course we will be finding roots of functions. a root of a function is nothing more than a number for which the function is zero. in other words, finding the roots of a function, g(x), is equivalent to solving. g(x) = 0. example 3 determine all the roots of f(t) = 9t3 − 18t2 6t.
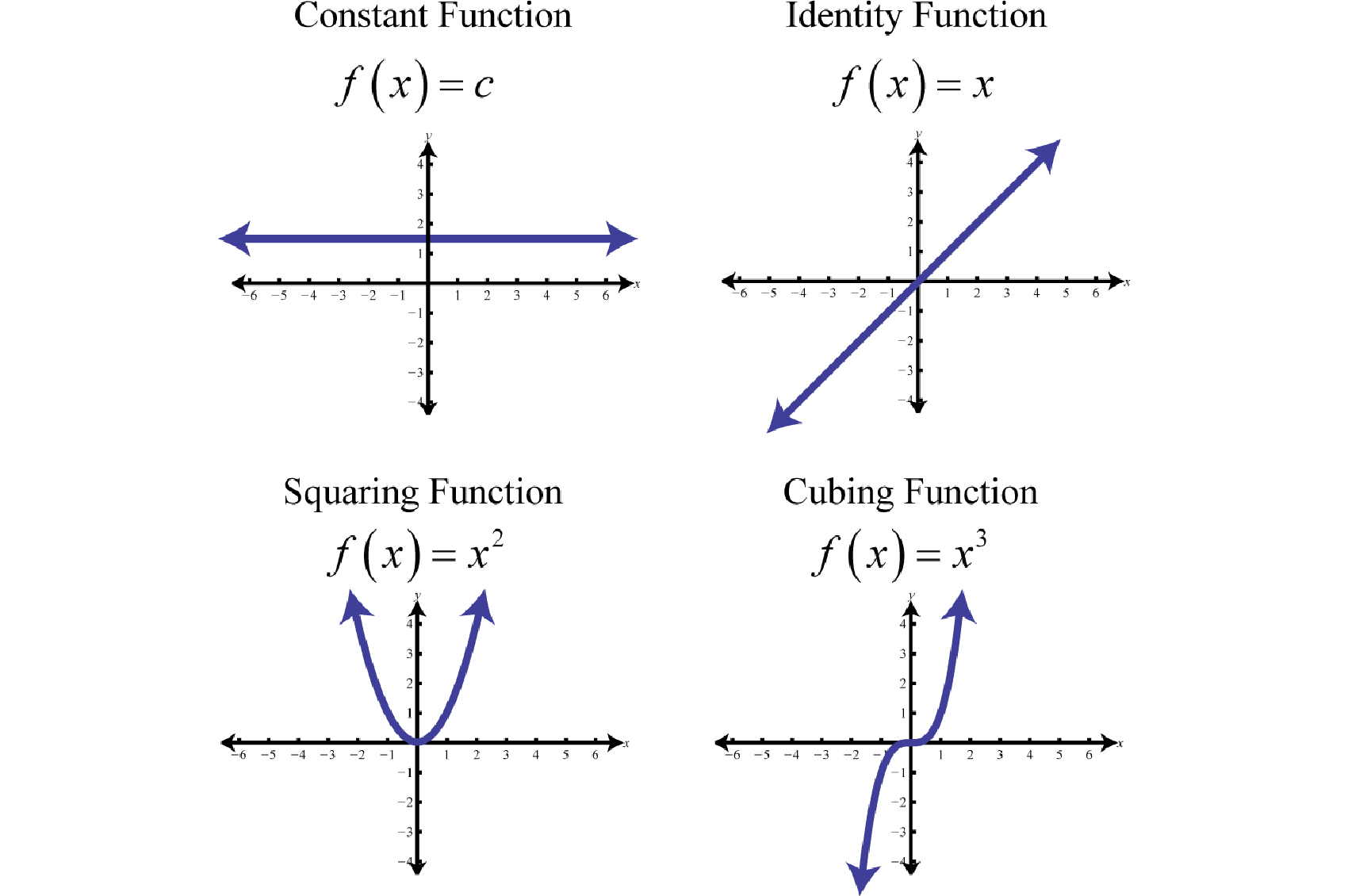
Graphing The Basic Functions Make new functions from two or more given functions. describe the symmetry properties of a function. in this section, we provide a formal definition of a function and examine several ways in which functions are represented—namely, through tables, formulas, and graphs. we study formal notation and terms related to functions. All throughout a calculus course we will be finding roots of functions. a root of a function is nothing more than a number for which the function is zero. in other words, finding the roots of a function, g(x), is equivalent to solving. g(x) = 0. example 3 determine all the roots of f(t) = 9t3 − 18t2 6t. The element of the first set is called the input; the element of the second set is called the output. functions are used all the time in mathematics to describe relationships between two sets. for any function, when we know the input, the output is determined, so we say that the output is a function of the input. Solving and evaluating functions. when we work with functions, there are two typical things we do: evaluate and solve. evaluating a function is what we do when we know an input and use the function to determine the corresponding output. evaluating will always produce one result, since each input of a function corresponds to exactly one output.
Day 1 Review Functions Part 1 Youtube The element of the first set is called the input; the element of the second set is called the output. functions are used all the time in mathematics to describe relationships between two sets. for any function, when we know the input, the output is determined, so we say that the output is a function of the input. Solving and evaluating functions. when we work with functions, there are two typical things we do: evaluate and solve. evaluating a function is what we do when we know an input and use the function to determine the corresponding output. evaluating will always produce one result, since each input of a function corresponds to exactly one output.

Comments are closed.