Basic Derivative Rules Calculus

Calculus Derivative Rules Video Lessons Examples Solutions The derivative tells us the slope of a function at any point. there are rules we can follow to find many derivatives. for example: the slope of a constant value (like 3) is always 0; the slope of a line like 2x is 2, or 3x is 3 etc; and so on. here are useful rules to help you work out the derivatives of many functions (with examples below). Differential calculus 6 units · 117 skills. unit 1 limits and continuity. unit 2 derivatives: definition and basic rules. unit 3 derivatives: chain rule and other advanced topics. unit 4 applications of derivatives. unit 5 analyzing functions. unit 6 parametric equations, polar coordinates, and vector valued functions. course challenge.

Derivative Rules Cheat Sheet Calculus Ace Tutors Blog To better understand the sequence in which the differentiation rules are applied, we use leibniz notation throughout the solution: f′ (x) = d dx(2x5 7) = d dx(2x5) d dx(7) apply the sum rule. = 2 d dx(x5) d dx(7) apply the constant multiple rule. = 2(5x4) 0 apply the power rule and the constant rule. = 10x4 simplify. 3.3.2 apply the sum and difference rules to combine derivatives. 3.3.3 use the product rule for finding the derivative of a product of functions. 3.3.4 use the quotient rule for finding the derivative of a quotient of functions. 3.3.5 extend the power rule to functions with negative exponents. 3.3.6 combine the differentiation rules to find the. Theorem 13 allows us to find the derivatives of a wide variety of functions. it can be used in conjunction with the power rule to find the derivatives of any polynomial. recall in example 36 that we found, using the limit definition, the derivative of \(f(x) = 3x^2 5x 7\). we can now find its derivative without expressly using limits:. It means that, for the function x 2, the slope or "rate of change" at any point is 2x. so when x=2 the slope is 2x = 4, as shown here: or when x=5 the slope is 2x = 10, and so on. note: f’ (x) can also be used to mean "the derivative of": f’ (x) = 2x. "the derivative of f (x) equals 2x". or simply "f dash of x equals 2x".

Calculus Derivative Rules Video Lessons Examples Solutions Theorem 13 allows us to find the derivatives of a wide variety of functions. it can be used in conjunction with the power rule to find the derivatives of any polynomial. recall in example 36 that we found, using the limit definition, the derivative of \(f(x) = 3x^2 5x 7\). we can now find its derivative without expressly using limits:. It means that, for the function x 2, the slope or "rate of change" at any point is 2x. so when x=2 the slope is 2x = 4, as shown here: or when x=5 the slope is 2x = 10, and so on. note: f’ (x) can also be used to mean "the derivative of": f’ (x) = 2x. "the derivative of f (x) equals 2x". or simply "f dash of x equals 2x". In this chapter we introduce derivatives. we cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well as derivatives of polynomials, roots, trig functions, inverse trig functions, hyperbolic functions, exponential functions and logarithm functions. we also cover implicit differentiation, related. Use basic differentiation rules to evaluate derivatives of combined functions. ap®︎ college calculus ab; derivative rules: constant, sum, difference, and.

Derivative Rules Power Product And Sum Rules Math Original In this chapter we introduce derivatives. we cover the standard derivatives formulas including the product rule, quotient rule and chain rule as well as derivatives of polynomials, roots, trig functions, inverse trig functions, hyperbolic functions, exponential functions and logarithm functions. we also cover implicit differentiation, related. Use basic differentiation rules to evaluate derivatives of combined functions. ap®︎ college calculus ab; derivative rules: constant, sum, difference, and.
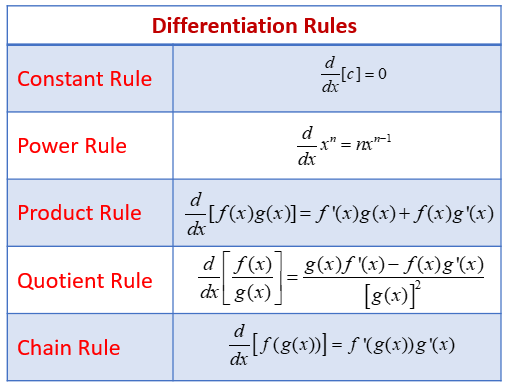
Examples Using The Derivative Rules With Formulas Videos
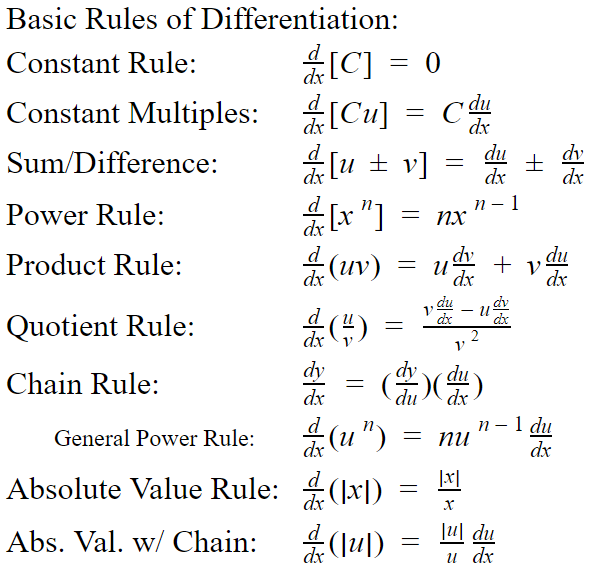
Derivative Rules Ap Calc Bc

Comments are closed.