Article 59 Geometry The Golden Ratio Part 4 Golden Spirals

Article 59 Geometry The Golden Ratio Part 4 Golden Spirals Remove successive squares from each golden rectangle and fill each square with a quarter arc. this produces the golden spiral. every segment has the same curvature, although the spiral size differs. remember, every square has the important 1:√2 ratio built into its form. if the side length = 1 then the diagonal = √2. The fibonacci spiral gets closer and closer to a golden spiral as it increases in size because of the ratio of each number in the fibonacci series to the one before it converges on phi, 1.618, as the series progresses (e.g., 1, 1, 2, 3, 5, 8 and 13 produce ratios of 1, 2, 1.5, 1.67, 1.6 and 1.625, respectively) fibonacci spirals and golden.

Article 59 Geometry The Golden Ratio Part 4 Golden Spirals The golden spiral has the special property such that for every 1 4 turn (90° or π 2 in radians), the distance from the center of the spiral increases by the golden ratio φ = 1.6180. for this to occur, cot b must take the value (which comes from solving our function): using this value, and taking the simple case where a = 1, our function becomes:. This resulting golden spiral is often associated with the nautilus spiral, but incorrectly because the two spirals are clearly very different. a golden spiral created from a golden rectangle expands in dimension by the golden ratio with every quarter, or 90 degree, turn of the spiral. this can be constructed by starting with a golden rectangle. The golden ratio. article 56 – golden ratio – part 1 – introduction; article 57 golden ratio – part 2 – fibonacci & lucas sequence; article 58 golden ratio – part 3 – fibonacci circles, golden triangles & rectangles; article 59 golden ratio – part 4 – golden spirals; article 60 golden ratio – part 5 – the golden ratio. The fibonacci sequence even plays a role in the subtle spirals you can see in the seed head of a sunflower. this is because of something known as the golden ratio, the golden section or the greek.

Article 59 Geometry The Golden Ratio Part 4 Golden Spirals The golden ratio. article 56 – golden ratio – part 1 – introduction; article 57 golden ratio – part 2 – fibonacci & lucas sequence; article 58 golden ratio – part 3 – fibonacci circles, golden triangles & rectangles; article 59 golden ratio – part 4 – golden spirals; article 60 golden ratio – part 5 – the golden ratio. The fibonacci sequence even plays a role in the subtle spirals you can see in the seed head of a sunflower. this is because of something known as the golden ratio, the golden section or the greek. The golden ratio is not simply represented in line segments. it can be extended into other realms of geometry to create golden rectangles, golden triangles, and most famously, the golden spiral. it is here that the golden ratio really shines. this golden spiral can be seen in pinecones, storm patterns, nautilus shells, and spiral galaxies. Definition of phi. phi can be defined by taking a stick and breaking it into two portions. if the ratio between these two portions is the same as the ratio between the overall stick and the larger.

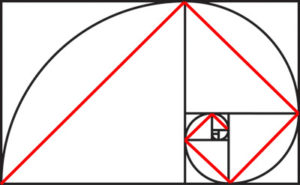
Article 59 Geometry The Golden Ratio Part 4 Golden Spirals The golden ratio is not simply represented in line segments. it can be extended into other realms of geometry to create golden rectangles, golden triangles, and most famously, the golden spiral. it is here that the golden ratio really shines. this golden spiral can be seen in pinecones, storm patterns, nautilus shells, and spiral galaxies. Definition of phi. phi can be defined by taking a stick and breaking it into two portions. if the ratio between these two portions is the same as the ratio between the overall stick and the larger.