Area Of Polygon Shoelace Formula
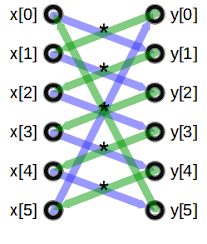
Area Of Polygon Shoelace Formula The shoelace formula, also known as gauss's area formula and the surveyor's formula, [1] is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their cartesian coordinates in the plane. [2] it is called the shoelace formula because of the constant cross multiplying for the coordinates making up the. We can compute the area of a polygon using the shoelace formula. area. = | 1 2 [ (x 1 y 2 x 2 y 3 … x n 1 y n x n y 1) –. (x 2 y 1 x 3 y 2 … x n y n 1 x 1 y n) ] |. the above formula is derived by following the cross product of the vertices to get the area of triangles formed in the polygon.
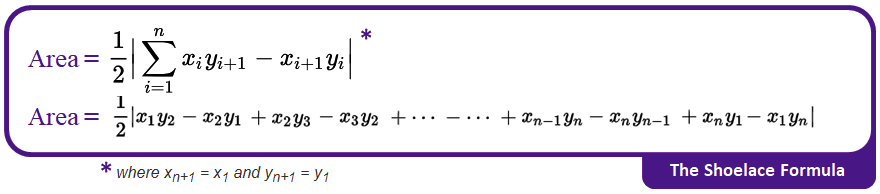
Area Of Polygon Shoelace Formula The shoelace formula, also known as gauss's area formula, the shoelace algorithm, shoelace method, or surveyor's formula, is a name sometimes given to the polygon area formula for the area of a simple polygon in terms of the cartesian coordinates of its vertices (x 1,y 1), , (x n,y n). This can also be written in form of a summation or in terms of determinants as which is useful in the variant of the shoelace theorem. note here that and . the formula may also be considered a special case of green's theorem where and so . proof 1. claim 1: the area of a triangle with coordinates , , and is . proof of claim 1:. Area = absolute of 0.5 ( 1×2 3×4 3×1 4×0 2×1 – 3×1 – 3×2 – 4×4 – 2×1 – 1×0) area = 4. let’s check again with wolfram alpha – and yes it does indeed have an area of 4. it could be a nice exploration task to take this further and to explore how many different methods there are to find the area of polygons – and. The shoelace algorithm 101 computing. the shoelace formula or shoelace algorithm is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their cartesian coordinates in the plane. the method consists of cross multiplying corresponding coordinates of the different vertices of a polygon to find its area.

Geo Polygon Area Shoelace Method Youtube Area = absolute of 0.5 ( 1×2 3×4 3×1 4×0 2×1 – 3×1 – 3×2 – 4×4 – 2×1 – 1×0) area = 4. let’s check again with wolfram alpha – and yes it does indeed have an area of 4. it could be a nice exploration task to take this further and to explore how many different methods there are to find the area of polygons – and. The shoelace algorithm 101 computing. the shoelace formula or shoelace algorithm is a mathematical algorithm to determine the area of a simple polygon whose vertices are described by their cartesian coordinates in the plane. the method consists of cross multiplying corresponding coordinates of the different vertices of a polygon to find its area. The shoelace formula (a.k.a. gauss's area formula) is a smart way of determining the area of a simple polygon (i.e., without self intersections). all you need to know is the cartesian coordinates of the vertices of the polygon. The shoelace theorem is named after the visual pattern formed when multiplying the coordinates, which resembles the lacing of a shoe. the theorem has roots in classical geometry and is particularly useful for finding the area of polygons in coordinate geometry. calculation formula. the shoelace theorem calculates the area of a polygon using the.

Comments are closed.