Area Of Parallelograms How To Find The Area Of A Parallelogram
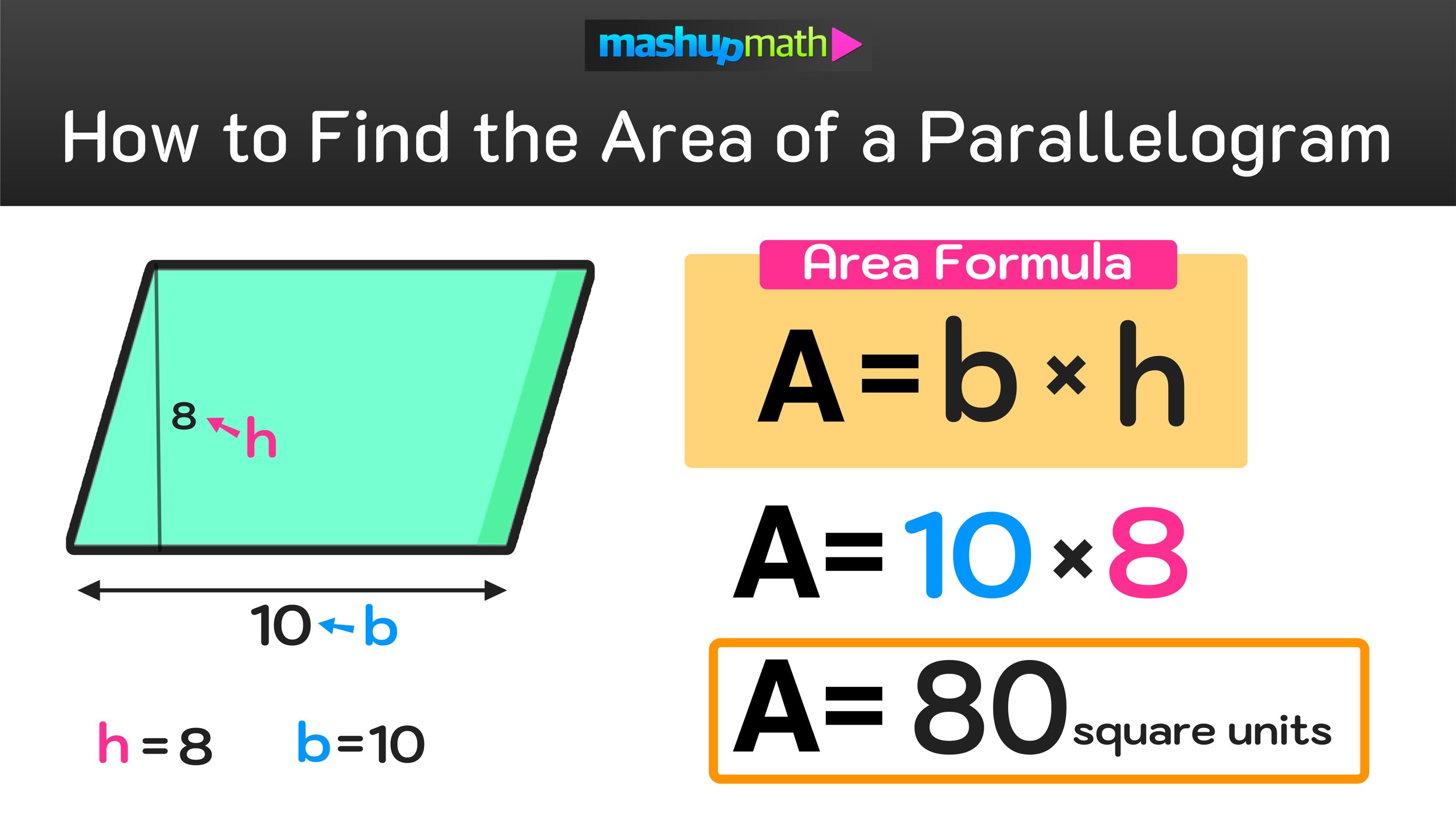
How To Find The Area Of A Parallelogram In 3 Easy Steps Mashup Math Hence, we get a = ab sin (x) let us solve some examples. find the area of a parallelogram whose adjacent sides are 3 cm and 4 cm, respectively. the angle between the two adjacent sides is 60°. solution: as we know, a = ab sin (x), here a = 3 cm, b = 4 cm, x = 60°. = 3 × 4 sin (60) = 12 ×. Assume that we want to calculate the area knowing the sides of a parallelogram and the angle between them. enter the given values to the right boxes. assume 5 in, 13 in, and 30° for the first side, the second one, and the angle between them, respectively. the calculator displays the area of a parallelogram value. it's 32.5 in² in our case.
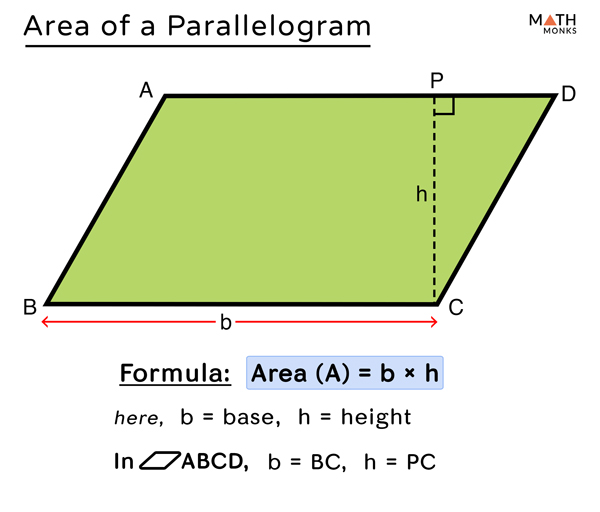
Area Of Parallelogram Formulas Diagrams Examples 1. multiply the base of the parallelogram by the height to find the area. if your problem gives you a measurement of the base and height of a parallelogram, simply multiply them to get your area. for example, if the base is 5, and the height 3, then your area is , since . Categories: calculating volume and area. to find the area of a parallelogram, use the formula area = bh, where b is the length of the parallelogram and h is the height. for example, if you were trying to find the area of a parallelogram that has a length of 10 and a height of 5, you'd multiply 10 by 5 and get 50. Suppose a and b are the set of parallel sides of a parallelogram and h is the height, then based on the length of sides and height of it, the formula for its area is given by: area = base × height. a = b × h [sq.unit] example: if the base of a parallelogram is equal to 5 cm and the height is 3 cm, then find its area. The area of a parallelogram can be calculated when the diagonals and their intersecting angle are known. the formula is given as, area = ½ × d 1 × d 2 sin (x), where 'd1' and 'd2' are lengths of diagonals of the parallelogram, and 'x' is the angle between them. q1: the parallelogram's height is thrice its base.

How To Calculate The Area Of A Parallelogram 3 Steps Suppose a and b are the set of parallel sides of a parallelogram and h is the height, then based on the length of sides and height of it, the formula for its area is given by: area = base × height. a = b × h [sq.unit] example: if the base of a parallelogram is equal to 5 cm and the height is 3 cm, then find its area. The area of a parallelogram can be calculated when the diagonals and their intersecting angle are known. the formula is given as, area = ½ × d 1 × d 2 sin (x), where 'd1' and 'd2' are lengths of diagonals of the parallelogram, and 'x' is the angle between them. q1: the parallelogram's height is thrice its base. Area formula using the sides and angle. if the side lengths and an angle of a parallelogram are given, the area is: a=a·b·sin (θ) where a and b are the lengths of the adjacent sides and θ is one of the angles. the area of a triangle with angle θ between sides a and b is . a diagonal of a parallelogram divides it into two congruent. A parallelogram is a flat shape with opposite sides parallel and equal in length. opposite sides are parallel. opposite sides are equal in length. opposite angles are equal (angles a are the same, and angles b are the same) angle a and angle b add up to 180°, so they are supplementary angles. play with a parallelogram:.
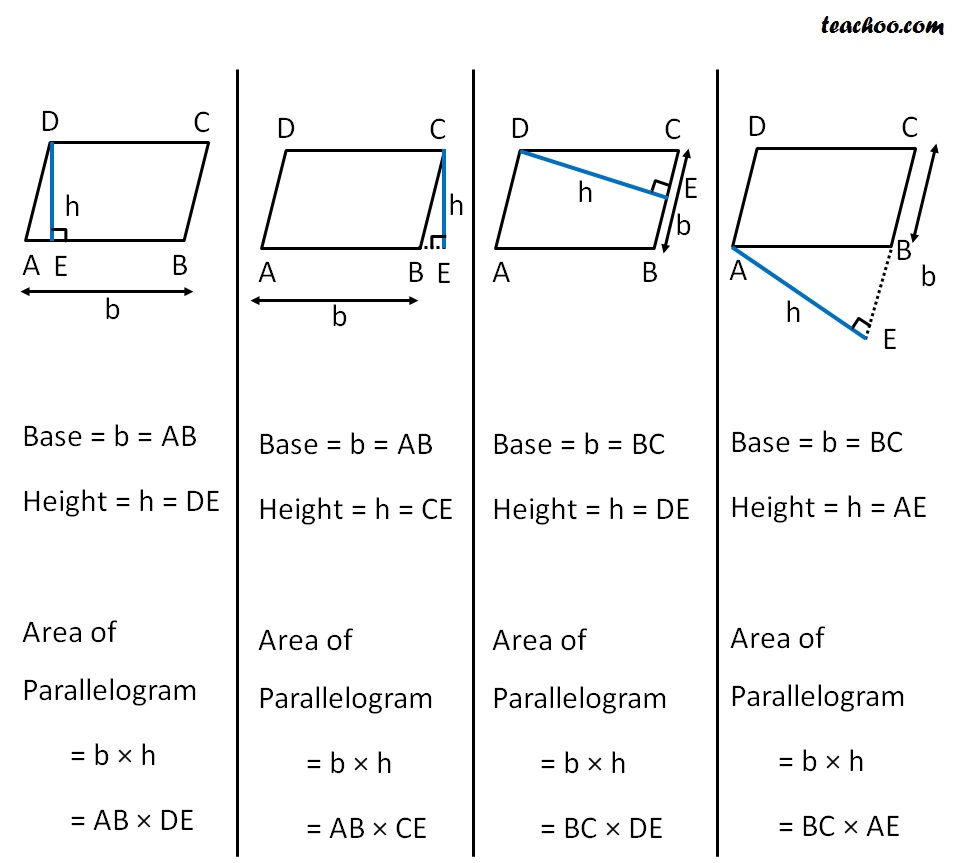
Area Of Parallelogram Formula With Examples Teachoo Area Of Para Area formula using the sides and angle. if the side lengths and an angle of a parallelogram are given, the area is: a=a·b·sin (θ) where a and b are the lengths of the adjacent sides and θ is one of the angles. the area of a triangle with angle θ between sides a and b is . a diagonal of a parallelogram divides it into two congruent. A parallelogram is a flat shape with opposite sides parallel and equal in length. opposite sides are parallel. opposite sides are equal in length. opposite angles are equal (angles a are the same, and angles b are the same) angle a and angle b add up to 180°, so they are supplementary angles. play with a parallelogram:.

Area Of Parallelogram Formula Vector Form Using Diagonals

Comments are closed.