Area Of A Parallelogram Formulas And Examples Neurochispas

Area And Perimeter Of A Parallelogram Formulas And Examples Area of a parallelogram using its diagonals. the area of any parallelogram can also be calculated with the lengths of its diagonals by using the following formula: a=\frac {d {1}\times d {2}\sin (y)} {2} a = 2d1×d2 sin(y) where, d {1}, ~ d {2} d1, d2 are the lengths of the diagonals and y is the angle of intersection of the diagonals. We can calculate the area of a parallelogram when we know the lengths of the diagonals and the angle of intersection of the diagonals. then, we use the following formula: a=\frac {d {1}\times d {2}\sin (y)} {2} a = 2d1×d2 sin(y) where, d {1}, ~d {2} d1, d2 are the lengths of the diagonals and y is the angle of intersection of the diagonals.

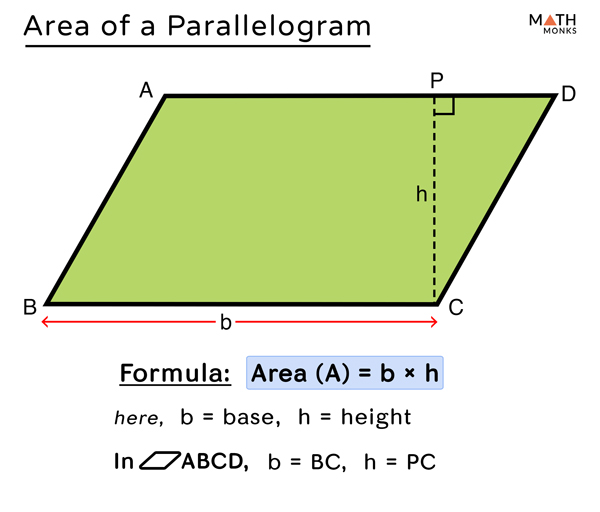
Area Of A Parallelogram Formulas And Examples Neurochispas Important formulas of parallelograms. the formulas for the area and perimeter of a parallelogram can be used to solve problems. area of a parallelogram. the area of the parallelogram is the region occupied by the figure in the two dimensional plane. the following is the formula to find the area of the parallelogram:. Hence, we get a = ab sin (x) let us solve some examples. find the area of a parallelogram whose adjacent sides are 3 cm and 4 cm, respectively. the angle between the two adjacent sides is 60°. solution: as we know, a = ab sin (x), here a = 3 cm, b = 4 cm, x = 60°. = 3 × 4 sin (60) = 12 ×. Example 2: calculate the area of a parallelogram whose diagonals are 15 units and 20 units, and the angle of intersection between the diagonals is 30°. solution: let d 1 = 15 units and d 2 = 20 units. using the formula for the area of a parallelogram with the lengths of its diagonals: area = $\frac{1}{2} \times d {1} \times d {2} \times sin(x)$. Example 1: decompose the parallelogram. decompose the parallelogram and rearrange its part so that they form a rectangle. then find the area. decompose the parallelogram into two triangles and a rectangle. 2 move one triangle to the opposite side of the parallelogram so that the shape is now a rectangle.

Area Of A Parallelogram Formulas And Examples Neurochispas Example 2: calculate the area of a parallelogram whose diagonals are 15 units and 20 units, and the angle of intersection between the diagonals is 30°. solution: let d 1 = 15 units and d 2 = 20 units. using the formula for the area of a parallelogram with the lengths of its diagonals: area = $\frac{1}{2} \times d {1} \times d {2} \times sin(x)$. Example 1: decompose the parallelogram. decompose the parallelogram and rearrange its part so that they form a rectangle. then find the area. decompose the parallelogram into two triangles and a rectangle. 2 move one triangle to the opposite side of the parallelogram so that the shape is now a rectangle. The area of a parallelogram can be calculated when the diagonals and their intersecting angle are known. the formula is given as, area = ½ × d 1 × d 2 sin (x), where 'd1' and 'd2' are lengths of diagonals of the parallelogram, and 'x' is the angle between them. q1: the parallelogram's height is thrice its base. Area formula using the sides and angle. if the side lengths and an angle of a parallelogram are given, the area is: a=a·b·sin (θ) where a and b are the lengths of the adjacent sides and θ is one of the angles. the area of a triangle with angle θ between sides a and b is . a diagonal of a parallelogram divides it into two congruent.
Area Of Parallelogram Formulas Diagrams Examples The area of a parallelogram can be calculated when the diagonals and their intersecting angle are known. the formula is given as, area = ½ × d 1 × d 2 sin (x), where 'd1' and 'd2' are lengths of diagonals of the parallelogram, and 'x' is the angle between them. q1: the parallelogram's height is thrice its base. Area formula using the sides and angle. if the side lengths and an angle of a parallelogram are given, the area is: a=a·b·sin (θ) where a and b are the lengths of the adjacent sides and θ is one of the angles. the area of a triangle with angle θ between sides a and b is . a diagonal of a parallelogram divides it into two congruent.

Comments are closed.