Area Of A Parallelogram Formula And Examples
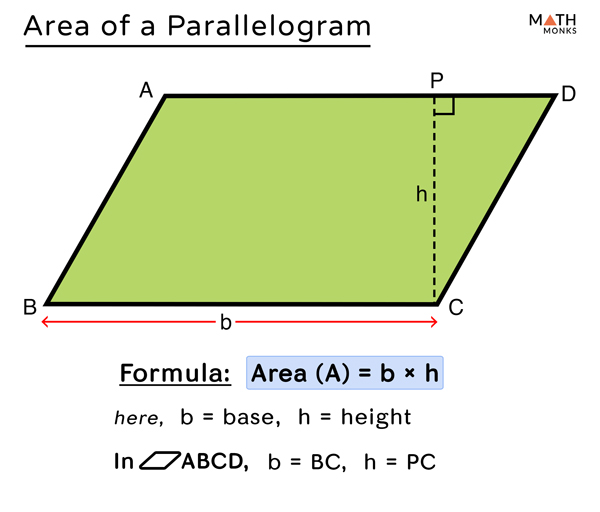
Area Of Parallelogram Formulas Diagrams Examples Hence, we get a = ab sin (x) let us solve some examples. find the area of a parallelogram whose adjacent sides are 3 cm and 4 cm, respectively. the angle between the two adjacent sides is 60°. solution: as we know, a = ab sin (x), here a = 3 cm, b = 4 cm, x = 60°. = 3 × 4 sin (60) = 12 ×. Area = base × height. a = b × h [sq.unit] example: if the base of a parallelogram is equal to 5 cm and the height is 3 cm, then find its area. solution: given, the length of base=5 cm and height = 3 cm. as per the formula, area = 5 × 3 = 15 sq.cm.
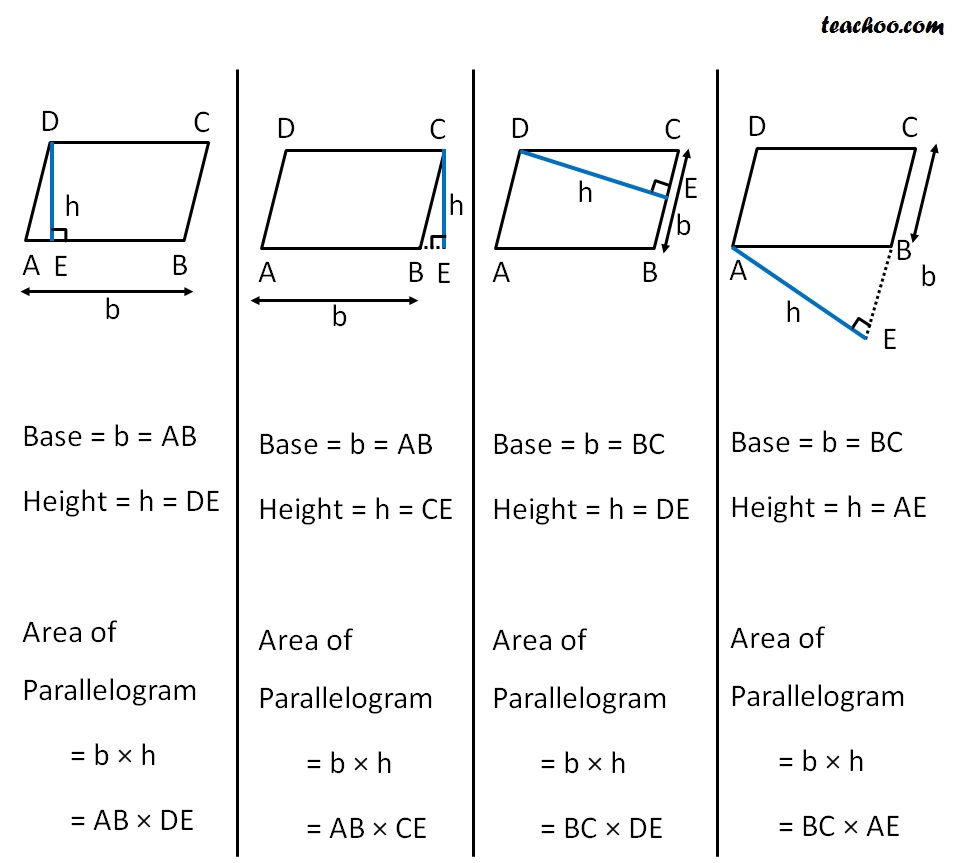
Area Of Parallelogram Formula With Examples Teachoo Area Of Para Example 2: calculate the area of a parallelogram whose diagonals are 15 units and 20 units, and the angle of intersection between the diagonals is 30°. solution: let d 1 = 15 units and d 2 = 20 units. using the formula for the area of a parallelogram with the lengths of its diagonals: area = $\frac{1}{2} \times d {1} \times d {2} \times sin(x)$. Example 1: decompose the parallelogram. decompose the parallelogram and rearrange its part so that they form a rectangle. then find the area. decompose the parallelogram into two triangles and a rectangle. 2 move one triangle to the opposite side of the parallelogram so that the shape is now a rectangle. The area of a parallelogram can be calculated when the diagonals and their intersecting angle are known. the formula is given as, area = ½ × d 1 × d 2 sin (x), where 'd1' and 'd2' are lengths of diagonals of the parallelogram, and 'x' is the angle between them. q1: the parallelogram's height is thrice its base. Here’s how it helps us find the area of the parallelogram. first, the area of the pink triangle would be – similarly, now, the area of the parallelogram would be the sum of the areas of the four triangles. or two times the sum of the two triangles shown above. formula derived!.
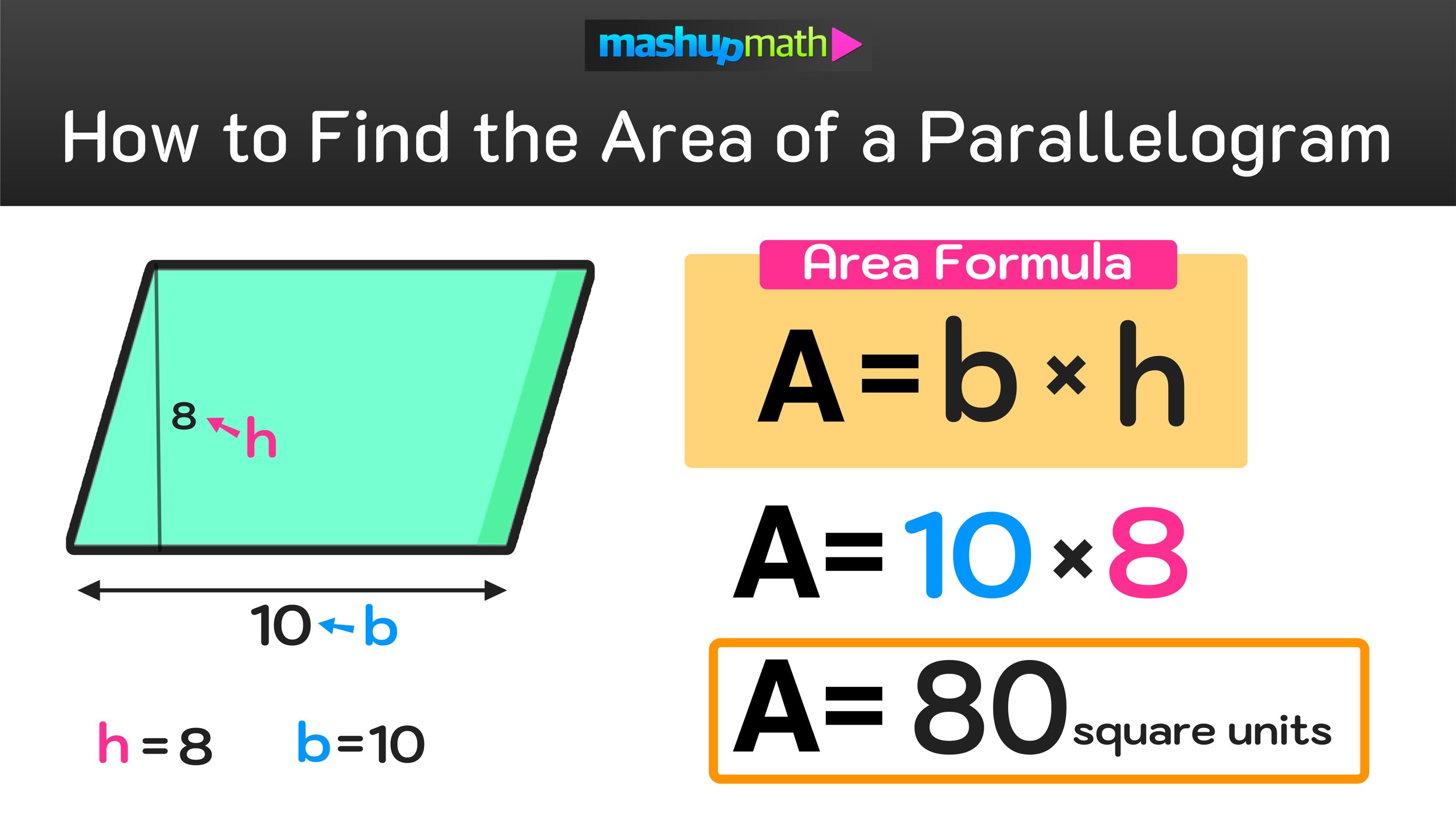
How To Find The Area Of A Parallelogram In 3 Easy Steps Mashup Math The area of a parallelogram can be calculated when the diagonals and their intersecting angle are known. the formula is given as, area = ½ × d 1 × d 2 sin (x), where 'd1' and 'd2' are lengths of diagonals of the parallelogram, and 'x' is the angle between them. q1: the parallelogram's height is thrice its base. Here’s how it helps us find the area of the parallelogram. first, the area of the pink triangle would be – similarly, now, the area of the parallelogram would be the sum of the areas of the four triangles. or two times the sum of the two triangles shown above. formula derived!. The 3 steps for how to find the area of a parallelogram: step one: identify the value of b (the base of the parallelogram) and h (the height of the parallelogram) step two: input the values of b and h into the area of a parallelogram formula, a = b x h, and solve for a. step three: write the final answer using square units. The area of parallelogram is 90 square inches. example 3: the total area of the parallelogram is 126 square feet. find the base of the parallelogram if the height of the parallelogram is 14 feet. solution: the height of the parallelogram is known. to find the base we use the area of a parallelogram formula to form an equation then solve.

Area Of Parallelogram Formula Vector Form Using Diagonals The 3 steps for how to find the area of a parallelogram: step one: identify the value of b (the base of the parallelogram) and h (the height of the parallelogram) step two: input the values of b and h into the area of a parallelogram formula, a = b x h, and solve for a. step three: write the final answer using square units. The area of parallelogram is 90 square inches. example 3: the total area of the parallelogram is 126 square feet. find the base of the parallelogram if the height of the parallelogram is 14 feet. solution: the height of the parallelogram is known. to find the base we use the area of a parallelogram formula to form an equation then solve.
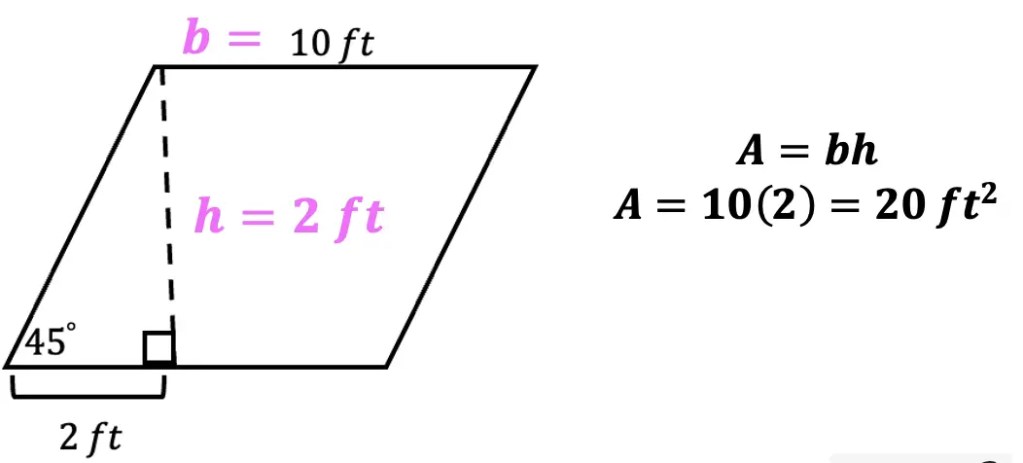
How To Find The Area Of A Parallelogram Geometry Math Lessons

Comments are closed.