Angulos Internos Y Externos De Poligonos Regulares Geogebra

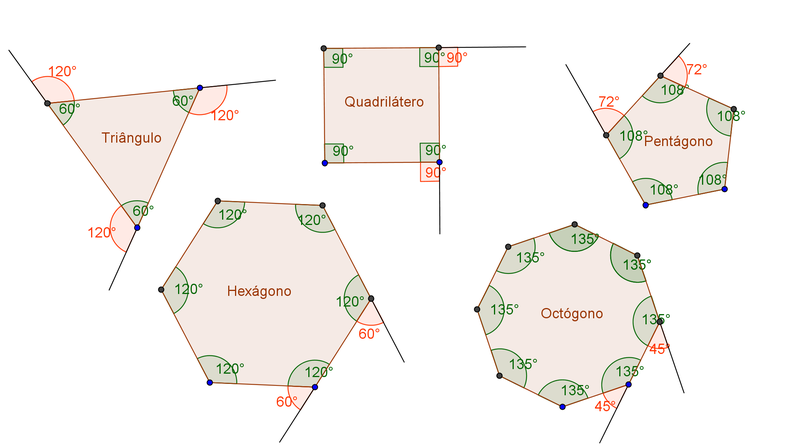
ángulos Internos Y Externos De Polígonos Regulares Geogebra Autor: nikruy. tema: Ángulos, polígonos. Ángulos internos y externos de polígonos regulares. estas imágenes nos muestran las características de los polígonos regulares, centro, radio, apotema, ángulo central, ángulos internos y externos. En conclusión, la medida del ángulo interno de un polígono regular se puede obtener utilizando dos expresiones algebraicas que son equivalentes: ángulo interno de un polígono regular = 180° 360° n. ángulo interno de un polígono regular = 180° (n – 2) n. Ángulos internos de polígonos regulares.

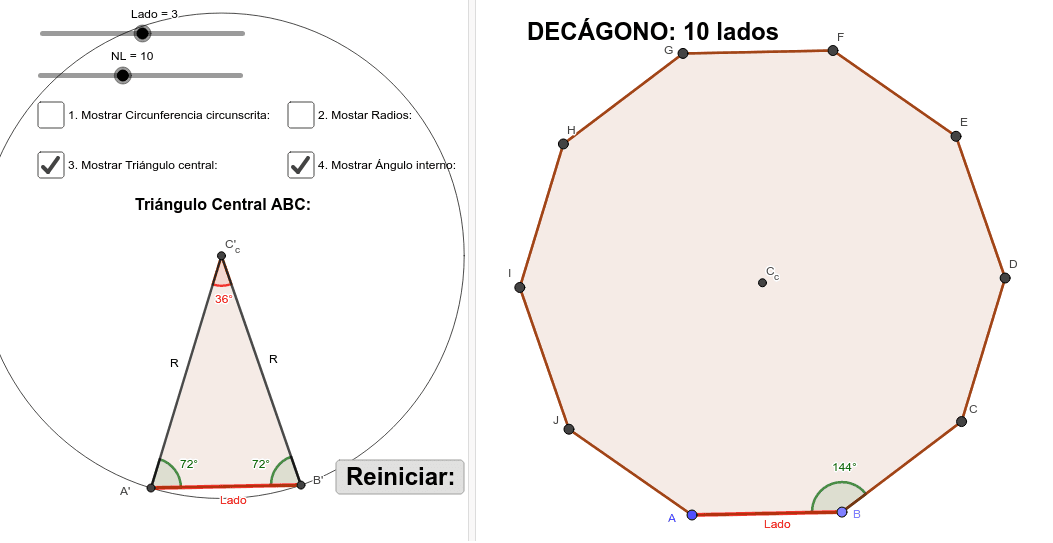
ángulos Internos De Polígonos Regulares Geogebra De este análisis se puede concluir que la suma de los ángulos internos de un polígono está dada por la fórmula: suma = 180° (n 2) donde n es el número de lados. si es un triángulo, n = 3: si es un cuadrado, n = 4: si es un octágono, n = 8: para descomponer el polígono se puede utilizar cualquiera de los vértices. Cálculo de ángulos internos. para calcular el ángulo interno de un polígono regular, se utiliza la fórmula: Ángulo interno = (n – 2) × 180 n. donde n es el número de lados del polígono. por ejemplo, para un hexágono (n=6): Ángulo interno = (6 – 2) × 180 6 = 120 grados. Construcciones de polígonos regulares. usa tu brújula para construir un círculo como el que se muestra a continuación en una hoja de papel. describe cómo doblar el papel dos veces para ayudarte a construir un cuadrado. figura 5.23.1. Ángulos internos y externos de un polígono. los ángulos internos de un polígono regular pueden ser calculados usando una fórmula. esta fórmula nos permite calcular su suma basados en el número de lados del polígono. por otra parte, la suma de los ángulos externos de cualquier polígono siempre es igual a 360°. entonces, la medida de.

Determinar Los ángulos Internos Y Externos De Un Polígonos Regular Construcciones de polígonos regulares. usa tu brújula para construir un círculo como el que se muestra a continuación en una hoja de papel. describe cómo doblar el papel dos veces para ayudarte a construir un cuadrado. figura 5.23.1. Ángulos internos y externos de un polígono. los ángulos internos de un polígono regular pueden ser calculados usando una fórmula. esta fórmula nos permite calcular su suma basados en el número de lados del polígono. por otra parte, la suma de los ángulos externos de cualquier polígono siempre es igual a 360°. entonces, la medida de. Ejemplo 3: polígono de 7 lados. para ilustrar la flexibilidad de la fórmula, consideremos un polígono irregular con 7 lados: suma de ángulos internos = (7 – 2) × 180° = 5 × 180° = 900°. en este caso, la suma de los ángulos internos de un polígono de 7 lados es 900°. esta capacidad de aplicar la fórmula a polígonos con diferentes. Podemos encontrar la suma de ángulos internos de cualquier polígono usando la siguiente fórmula: (n − 2) × 1 8 0. (n 2)\times 180 (n − 2) × 180 °. en donde, n es el número de lados del polígono. por ejemplo, usamos n=5 n = 5 para un pentágono. esta fórmula funciona sin importar si el polígono es regular o irregular.